星座图与IQ调制总结+BPSK、QPSK、8PSK、16QAM等的区别与总结

PSK
1.PSK是相移键控，分为BPSK、QPSK、8PSK。BPSK即2PSK，QPSK即4PSK。
2.对于MPSK可以认为是把单位圆分成了M个部分。
3.PSK是点都在同一个圆上，呈圆形排列，幅度相同，差别只在于相位。

1.1 BPSK

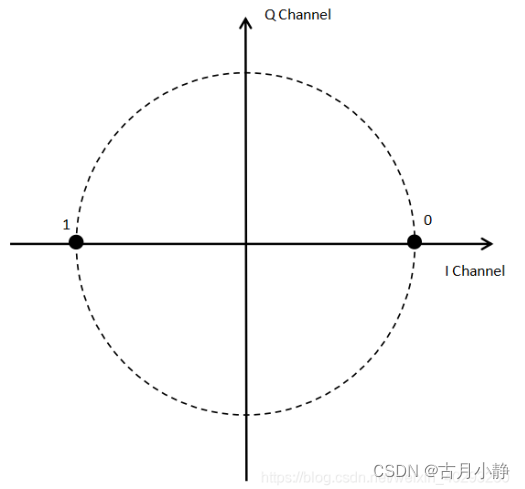
BPSK是二相相移键控，2=2^1，传输一个符号为传输一个bit的数据，输入信号只有0或1。
此时IQ平面被对称两个点的连线分为两半。

1.2 用IQ调制实现BPSK

从这个图是把Q轴和I轴都单独拿出来了。从星座图点分别向两个轴做垂线，得到两个轴对应的取值。
可以看出，BPSK中I有两种取值，而Q只有一种取值，就是0。
取值表如下：

注意，这里输入的原始信息只有0和1，是在映射后才有了+1和-1.

2.1QPSK

QPSK是四相相移键控，4=2^2，传输一个符号为传输2bit的数据。
此时四个点分别两两关于原点对称，将对称点连线，IQ平面被分为4半。

2.2 用IQ调制实现QPSK

QPSK在用IQ调制实现时，I和Q分别有两个取值，组合出4个点。
看到这里或许会有种错觉，是不是I的取值和Q的取值相乘就可以得到星座图点数。
但8PSK推翻了这种错觉。
取值表如下：

3.1 8PSK

8PSK是八相相移键控，8=2^3，传输一个符号为传输3bit的数据。
此时八个点分别关于原点有四对对称，将对称点连线，IQ平面被分为8半。

3.12 用IQ调制实现8PSK

在8PSK中，I和Q都有四种取值，但是组合出8种结果。因为I中不是每一个点都和Q中所有点做了组合。
取值表如下：

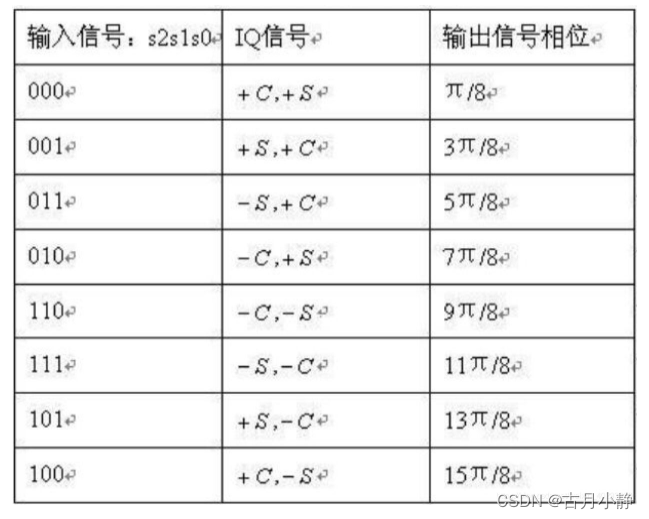
目前采用的排列方式是格雷码。
由于从概率角度来说，误判为相邻点的概率要大于误判为相对点的概率。
采用格雷码使每相邻的状态间一般只有一位不同，这样可以减少出错的概率。

QAM
1.QAM比较常见的有16QAM、64QAM。
2.QAM的点不在圆上，呈矩形排列，幅度不相同，相位也不相同。或者说但凡幅度相同的相位必然不同，凡相位相同的幅度必不同。这样就使QAM容纳了更多的点，所以QAM的优点也在于其具有更大的符号率，从而能传输效率就越高。但同时，星座点间距离越近也决定了误码率会增加。

2.1 16QAM
2^4 = 16，16QAM中每个符号代表4个bit。

QAM也可以将IQ轴单独拿出来看，用图上这种排列方式举例，最右边的一列I代表从左向右第1和3位分别为0和1，即0x1x，然后再与Q组合得到四个不同的状态。

2.2 64QAM
2^6 = 64，64QAM中每个符号代表6个bit。

当数据被输入，会被分成两路，一路作为I，一路作为Q。每个符号代表6个bit，则I路占三个bit，Q路有三个bit。将两路组合得出最后的点，也得出最后点代表的6bit序列。
当接收到点时，我们会根据欧氏距离最小来判定其究竟是哪个点，从而得到其代表的二进制序列段。

原文链接：https://blog.csdn.net/weixin_40293250/article/details/106246728