《吴恩达深度学习》学习笔记（中）

最新推荐文章于 2025-04-30 15:03:34 发布

海盗儿

最新推荐文章于 2025-04-30 15:03:34 发布

阅读量840

点赞数 8

文章标签：深度学习学习笔记

本文链接：https://blog.csdn.net/weixin_41554699/article/details/145815057

版权

这一篇学习笔记可能会包含以下内容：参考 https://zhuanlan.zhihu.com/p/531271576

第一周：深度学习的实践层面
- 训练集/开发集/测试集的划分
- 偏差与方差
- 机器学习的基础改进流程
- 正则化
- 输入归一化
- 梯度问题与带权初始化
- 梯度检查

第二周：优化算法
- 分批梯度下降
- 更高级的梯度下降算法
- 学习率衰减

第三周：调整超参数、批归一化和编程框架
- 调参策略
- 批归一化
- 多分类问题
- 深度学习框架 TensorFlow

优化神经网络

一. 训练集/开发集/测试集的划分

在使用机器学习的数据集时，我们一般把数据集分成三份：训练集、开发集、测试集。

机器学习是比深度学习的父集，表示一个更大的人工智能算法的集合。

开发集(Development Set) 另一种常见的称呼是验证集(Validation Set),即保留交叉验证(Hold-out Cross Validation)。

1.1 三种数据集的定义

它们三者的区别如下：

	训练集	开发集	测试集
用于优化参数	是	否	否
训练时可见？	是	是	否
最终测试时可见？	是	是	是

训练集就是令模型去拟合的数据。对于神经网络来说，我们把某类数据集输入进网络，之后用反向传播来优化网络的参数。这个过程中用的数据集就是训练营。

开发集是我们在训练时调整超参数时用到的数据集。我们会测试不同的超参数，看看模型在开发集上的性能，并选择令模型开发集上最优的一组超参数。

测试集是我们最终用来评估模型的数据集，当模型在测试集上评测时，我们的模型已经不允许修改了。我们一般把模型在测试集上的测评结果作为模型的性能评估标准。

在我们之前实现的小猫分类项目中，准确来说，我们使用的不叫测试集，而叫做开发集，因为我们是根据那个"testing set"优化网络超参数的。

有人把训练集比作上课，开发集比作作业，测试集比作考试。如果你理解了这三个数据集的原理，会发现这个比喻还是挺贴切的。事实上，由于测试集不参与训练，一个机器学习项目可以没有测试集，就像我们哪怕不经过考试，也可以学到知识一样。

1.2通过划分数据得到训练/测试集

在前一个机器学习纪元，人们通常会拿到一批数据，按7:3的比例划分训练集/测试集（对于没有超参数要调的模型），或者按6:2:2的比例划分训练集/开发集/测试集。

而在深度学习时代，数据量大大增加。实际上，开发集和测试集的目的都是评估模型，而评估模型所需的数据没有训练需要得那么多。所以，当整体的数据规模达到百万级，甚至更多时，我们只需要各取10000组数据作为开发集和测试集即可。

1.3收集来自不同分布的数据集

除了从同一批数据中划分出不同的数据集，还有另一种得到训练集、测试集的方式——从不同分布中收集数据集。

分布是统计学里的概念，这里可以理解成不同来源，内容的“平均值”差别很大的数据。

比如，假如我们要为某个小猫分类器收集小猫的图片，我们的训练图片可以是来自互联网，而开发和验证的数据来自用户用收集拍摄的图片。

注意，由于开发集和验证集都是用来评估的，它们应该来自同一个分布。

1.4偏差与方差

机器学习中，我们的模型会出现高偏差或/和高误差的问题。我们需要设法判断我们的模型是否有这些问题。

偏差(bias)与方差(variance)是统计学里的概念，前者表示一组数据离期待的平均值的差距，后者表示数据的离散程度。

试想一个射击运动员在打靶。偏差与打靶的总分数有关，因为总分越高，意味着每次射击都很靠近靶心；方差与选手的发挥稳定性有关，比如一个不稳定的选手可能一次9环，一次6环。

高偏差意味着模型总是不能得到很好的结果，高方差意味着模型不能很好地在所有数据集上取得好的结果（即只能在某些特定数据集上表现较好，在其他数据集上都表现较差）

我们把高偏差的情况叫做“欠拟合”（可能模型还没有训练完，所以表现不够好），把高方差的情况叫做“过拟合”（模型在训练集上训练过头了，结果模型只能在训练集上有很好的表现，在其他数据集上表现偶读不好）。

分别是前拟合，“恰好”，过拟合三种情况。

对于欠拟合的情况来说，一条直线并不足以把两类点分开，这个模型的整体表现较差。

对于过拟合的情况来说，模型过分追求训练集上的正确，结果产生了一条很奇怪的曲线。由于训练数据是有噪声（数据的标签不完全正确）的，这样的模型在真正的测试上可能表现不佳。

让我们人类来划分的话，最有可能给出的是中间那种划分结果。在这个模型中，虽然有些训练集中的点划分错了，但我们会认为这个模型在绝大多数数据上更合适。当我们用更多的测试数据来测试这个模型时，中间那幅图的测试结果肯定是这三种中最好的。

要判断机器学习模型是否存在高偏差或高方差的现象，可以去观察模型的训练集误差和开发集误差。以下是一个判断示例：

情况	1	2	3	4
训练集误差	1%	15%	0.5%	15%
开发集误差	11%	16%	1%	30%
诊断结果	高方差	高偏差	低误差、低方差	高误差、高方差

也就是说，如果开发集和训练集的表现差很多，就说明是高方差；如果训练集上的表现都很差，就是高偏差。

上面这些结论建立在最优误差——贝叶斯误差(Beyas Error)是0%的基础上下的判断。很多时候，仅通过输入数据中的信息，是不足以下判断的。比如告诉一个人是长头发，虽然这个人大概率是女生，但我们没有100%的把握说这是女生。如果我们知道人群中留长发的90%是女生，10%是男生，那么在这个“长头发分辨性别”的任务里的贝叶斯误差就是10%。
假如上面那个任务的贝叶斯误差是15%，那么我们认为情况2也是一个低误差的情况，因为它几乎做到了最优的准确率。

1.5改进机器学习的基本方法

首先检查高偏差问题。如果模型存在高偏差，则应该尝试使用更复杂的网络、更多增加训练时间。

确保模型没有高偏差问题后，才应该开始检查模型的方差。如果模型存在高方差，则应该增加数据或使用正则化。

此外，使用更合理的网络架构，往往对降低误差和方差都有效。

1.6正则化

其实正则化的意思就是“为防止过拟合而添加额外信息的过程”。在机器学习中，一种正则化方法是给损失函数添加一些与参数有关的额外项，以调整参数在梯度下降中的更新过程。正则化的数学原理我们会在下一节里学习，这一节先认识一下正则化是怎么操作的。

对于简单的逻辑回归，我们应该如何加正则化项：

原本的逻辑回归损失函数是：

$J\left ( w,b \right )=\frac{1}{m}\sum_{i=1}^{m}L\left ( \hat{y},y \right )$

现在我们给它加一个和参数 $w$ 有关的项

$J\left ( w,b \right )=\frac{1}{m}\sum_{i=1}^{m}\left ( L\left ( \hat{y,y} \right ) +\frac{\lambda }{2m}\left \| w^{2} \right \|_{2}\right )$

右侧这个 $\frac{\lambda }{2m}\left \| w^{2} \right \|_{2}$ 就是额外加进来的正则项。其中 $\lambda$ 是一个可调的超参数， $\left \| w \right \|_{2}^{2}$ 表示计算向量 $w$ 的I2范数。即：

$\left \| w \right \|_{2}^{2}=\sum_{j=1}^{n_{x}}w_{j}^{2}$

也就是说，某向量的l2范数就是它所有分量平方再求和。

类似地，其实向量也有1范数，也可以用来做正则化：

$\left \| w \right \|_{1}=\sum_{j=1}^{n_{x}}w_{j}$

1范数就是向量所有分量取绝对值再求和。

使用1范数做正则化会导致参数中出现很多0。人们还是倾向使用l2范数做正则化。

看到这里，大家或许会有问题： b也是逻辑回归的参数，为什么 w有正则项， b就没有？实际上，要给 b 加正则项也可以。但是在大多数情况下，参数 w 的数量远多于 b ，和 w 相关的正则项几乎不会影响到最终的损失函数。为了让整个过程更简洁一些， b 的正则项就被省略了。

推广到神经网络时，添加正则项的方法是类似的，只不过参数w变成了矩阵，所以正则项是：

$\frac{\lambda }{2m}\sum_{l=1}^{L}\left \| W^{[l]} \right \|_{F}^{2}$

其中 $\left \| W^{[l]} \right \|_{F}^{2}=\sum_{i=1}^{n^{[l]}}\sum_{j=1}^{n^{[l-1]}}(W_{ij}^{[l]})^{2}$

这种矩阵范数叫做Frobenius范数，叫它F-范数就行了。

如之前的文章所述，对于梯度下降算法来说，定义损失函数的根本目的是为了对参数求导。当参数 W 在损失函数里多了一项后，它的导数会有怎样的变化呢？

对于某参数向量w 来说，其实它的导数就多了一项：

$(\frac{\lambda }{2m}w^{2}){}'=\frac{\lambda }{m}w$

最终，参数向量w 会按如下的方式更新：

$w:=w-\alpha (dw+\frac{\lambda }{m}w)$

$w:=(1-\frac{\alpha \lambda }{m})w-\alpha dw$

仔细一看，其实相较之前的梯度更新公式，只是w 的系数从1 变成了 $(1-\frac{\alpha \lambda }{m})$ 。因此，用l2范数做正则化的方法会被称为 “权重衰减(Weight Decay)” , $\lambda$ 在某些编程框架中直接就被叫做weight decay。

1.7为什么正则项可以减小方差

这个曲线之所以能够那么精确地过拟合，是因为这个曲线的参数过多。如果这个曲线的参数少一点，那么它就不会有那么复杂的形状，过拟合现象也会得到缓解。

也就是说，如果神经网络简单一点，每个参数对网络的影响小一点，那么网络就更难去过拟合那些极端的数据。

添加了正则项后，网络的参数都受到了一定的“惩罚”。因此，参数会倾向于变得更小，从而产生刚刚提到的减轻过拟合的效果。

1.8DropOut

还有一种常用的正则化方法叫做 dropout，即随机使神经网络中的一些神经元“失活”。如下图所示：

我们可以领所有神经元在每轮训练中有50%的几率失活。在某轮训练中，神经网络的失活情况可能会像上图中下半部分所示：那些打叉的神经元不参与计算和，整个神经网络变得简单了许多。

在实际中，常常使用一种叫“inveted dropout”的实现方法。inverted dropout思想是：

对于神经网络的每一层，生成一个有哪些神经元失活的“失活矩阵”，再用这个矩阵去乘以这一层的激活输出（做乘法即领没有失效的激活保持原值，失效的激活取0）

d = np.random.rand(a.shape[0], a.shape[1]) < keep_prob
a = a * d
a /= keep_prob

这段代码中，d是失活矩阵。该矩阵通过一个随机数矩阵和一个保留概率keep_prob做小于运算生成。

np.random.rand 可以生成一个矩阵，其中矩阵中每个数都会均匀的随机出现在0～1之间。这样每个数小宇keep_prob的概率都是keep_prob。比如keep_prob=0.8 ,那么每个神经元都有80%的几率得到保留，20%的几率被丢弃。

做完小于运算之后，d其实是一个bool值矩阵。拿bool矩阵和一个普通的矩阵做逐对乘法，就等于bool矩阵为True的地方取普通矩阵的原值，bool矩阵为False的地方取0。

最后，得到了丢弃掉某些神经元的激活输出a后，我们还要做一个操作a /= keep_prob 。可以想象，如果我们丢掉了一些神经元，那么整个激活输出的“总和”的期望会变小。比如

keep_prob 为0.8，那么整个输出的大小都近似会变为原来的0.8倍。为了让输出的期望不变，我们要把激活输出除以keep_prob 。

如前文所强调地，dropout一次是对一层而言的。也就是说，每一层可以有不同的keep_prob。

dropout可能对损失函数变化曲线产生影响。一般调试时，如果损失函数一直在降，就说明训练算法没什么问题。但是，加入dropout后，由于每次优化的参数不太一样了，损失函数可能不会单调递减。因此，为了调试神经网络，可以先关闭dropout。确定损失函数确实在下降后，再开启它。

由于在CV（计算机视觉）中，图像的输入规模都很大，数据不足而引起过拟合是一件常见的事。因此，dropout在CV中被广泛应用。

注意，dropout是一种训练策略。在测试的时候，不需要使用dropout。

为什么dropout能够生效。有了dropout，意味着神经网络的权重不能集中在部分神经元上，因为某个神经元随时都可能会失效。因此，神经网络的权重会更加均衡。更加平均，意味着计算参数平方的I2会更小。也就是说，dropout令参数更平均，起到了和刚刚添加l2正则类似的效果。

1.9其他正则化方法

1.数据增强

比如对于一幅图片，我们可以翻转、旋转、缩进，以生成“更多”的训练数据。

2.提前停止

随着训练的进行，网络的损失函数可能越来越小，但开发集上的error会越来越高。只是因为训练得越久，参数就会越来越大，即越来越倾向于过拟合。提早结束训练，能够让参数取到一个合适的值。

提前中止也有一些不好的地方。在机器学习中，训练模型可以分成两部分：让损失函数更小、防止模型过拟合。我们通常会对这两部分独立地进行优化，即控制优化方法不变，改变正则化方法；或者改变减小梯度的算法，保证模型不进行任何正则化操作。而提前中止实际上混淆了减小损失函数和防止模型过拟合这两件事，不利于采取更多的调试策略。

3.输入归一化(Normalization)

假设如果左一图所示，每个输出张量长度为2，即两个分量： $x_{1},x_{2}$ 。我们可以认为每个输入向量就是一个二维平面上的点。统计完了所有样本，我们或许可以发现所有样本的 $x_{1}\in [0,5]$

$x_{2}\in [0,3]$ 这两个区间，两个区间长度不一。而且，数据在x1上比较分散和在x2上比较靠拢。这个训练样本显得非常凌乱。如果我们让输入归一化，使输入向量的每一个分量都满足了正态分布，难么这些数据可能会长得像图3.这样，数据分布的区间不仅长度相同，而且离散的程度也相同了。归一化可以通过以下方式实现：

$\mu =\frac{1}{m}\sum_{i=1}^{m}x^{(i)}$

$x:=(x-\mu )$

$\sigma ^{2}=\frac{1}{m}\sum_{i=1}^{m}(x^{(i)})^{2}$

$x:=x/\sigma$

注意，上式中我们计算方差时没有减均值，这是因为第二步更新的时候均值已经被减掉了

简单概括这个数学公式，就是“减均值，除方差”。

如果输入数据在各个分量上更加均匀，梯度下降的优化会更加便捷。

这里直接记住这个结论，不用过于在意它的数学原理。一种比较直观的解释是：如果分量大小不一，则参数w的每个分量的“作用”也会大小不一。如果w的每个分量都按差不多的“步伐”进行更新，那些“影响力更大”的w分量就会更新得过头，而“影响力更小”的w分量就更新得不足。这样，梯度下降法要耗费更多步才能找到最优值。如下图更新切面经过处理之后。

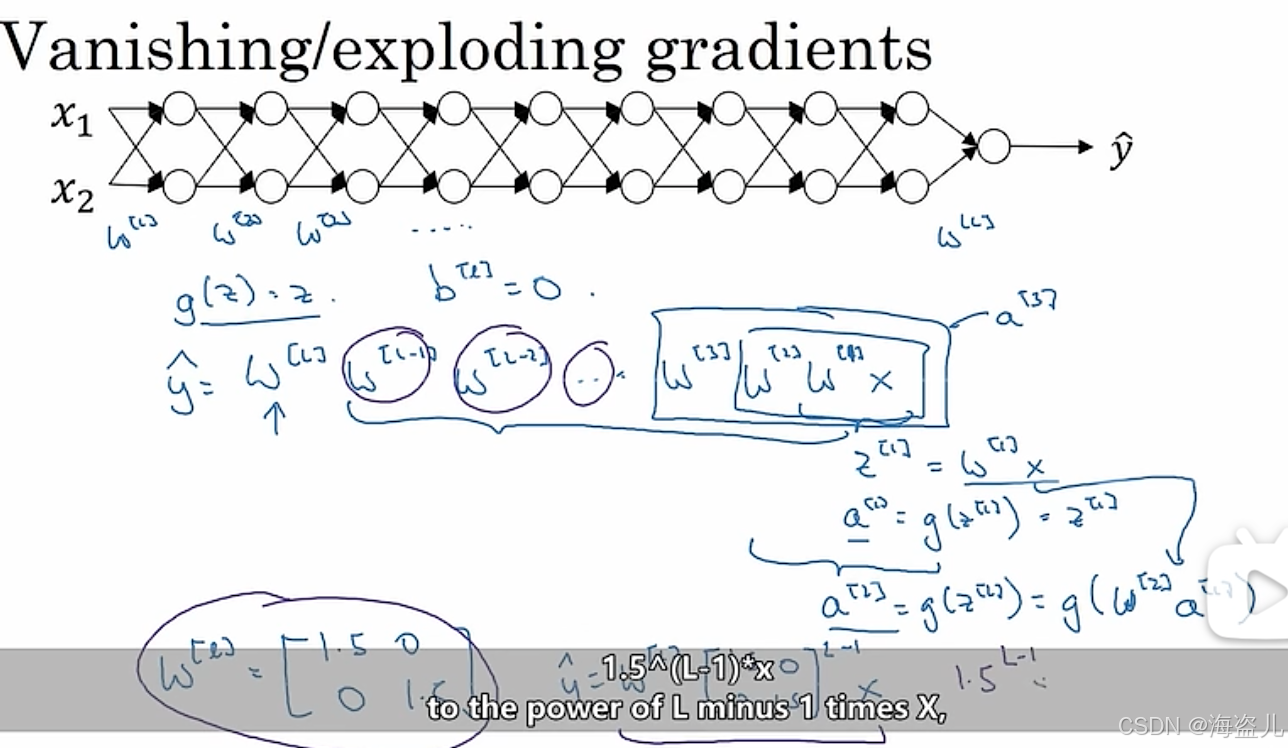
1.10梯度爆炸/弥散

如果一个神经网络的层数过深，可能会出现梯度极大或极小的情况，让我们看看这是怎么回事。

假设我们有上图这样一个很深的神经网络。我们取消所有的激活函数（ $g\left ( x \right )=x$ ）取消所有参数（即），那么这个网络的公式就是 $\hat{Y}=A=W^{L}W^{L-1}...W^{1}X$

其中 $W^{L-1}...W^{1}$ 都是2*2的矩阵，我们不妨假设他们都是同样的矩阵，那么上式可以写成

$Y=A= W^{L}(W)^{(L-1)}X$

如果W是这个样子：

$W=\begin{bmatrix} 1.5 & 0\\ 0 & 1.5 \end{bmatrix}$

那么经过次矩阵乘法后，这个矩阵就变成这个样子：

$W^{L-1}=\begin{bmatrix} 1.5^{L} & 0\\ 0 &1.5^{L} \end{bmatrix}$

由于这里的数值是随着成指数增长的，稍微取一个大一点的值，最后算出来的就会特别大。回顾一下前面的知识，最后一层的，而又是和相关的。最后的很大，会导致所有算出来的梯度都很大。

同理，如果矩阵里的数不是1.5，而是0.5，那么整个公式的数值就会指数级下降，从而导致梯度近乎“消失”。

1.11梯度问题的解决方法——加权初始化

我们刚刚讲到，梯度会爆炸或者弥散，本质原因是矩阵W的“大小”大于了1或者小于了1，从而使最后的计算结果过大或过小。但反过来想，如果我们令每一层的输出 A 的“大小”都在1附近，那么是不是就不会有梯度指数级变化的问题了呢？

让我们来看看该如何让每层输出 $A^{[l]}$ 都保持一个合适的值。我们考察

$Z=w_{1}x_{1} + w_{2}x_{2} ... + w_{n}x_{n}$

这个简单的网络。从直觉上看，如果n 越大，则公式里的项越多，Z 也越大。事实上，用统计学知识计算过后，能知道：若 $w_{i}$ 都是满足标准正态分布的，则 Z 的方差是n 。我们不希望 n的值太大或太小，希望能通过修改 $w_{i}$ 的大小，让 Z 的方差尽可能等于1。

为了做到这一点，我们可以在 $w$ 的初始化方法上做一点文章，我们可以改变 $w$ 的方差，以改变Z的方差。其实，我们只需要令 $w$ 的方差为 $\frac{1}{n}$ 就行了。用代码表示就是这样的：

W_l = np.random.randn(shape) * np.sqrt(1 / n[l-1])

这里n[l-1] 是第l层参数矩阵W_l 的长度，即每个参数向量w 的长度。

但由于每一层的输入不是Z，而是 $A = g(Z)$ ,我们在算方差时还要考虑到激活函数g的影响。

使用 Relu 时，初始化的权重用np.sqrt(2/ n[l-1]) 比较好，即用下面的代码：

W_l = np.random.randn(shape) * np.sqrt(2 / n[l-1])

对于tanh函数，令权重为np.sqrt(1 / n[l-1])，

这叫做 Xavier Initialization。还有研究表明用 np.sqrt(2 / (n[l-1]+n[l])) 也行。

总结一下，为了缓解梯度爆炸或梯度弥散的问题，可以对参数使用加权初始化。只需要初始化时多乘一个小系数，这个问题就能很大程度上有所缓解。

1.12梯度检查

进行深度学习编程时,梯度计算时比较容易出BUG的地方，我们可以用一种简单的方法来近似估计一个函数的导数，并将其与我们算出来的导数做一个对比，看看我们的导数计算函数有没有写错。

导数估计公式如下：

$f{}'(\theta )\approx \frac{f\left ( \theta +\varepsilon \right )-f\left ( \theta +\epsilon \right )}{2\epsilon }$

这个式子随 $\epsilon$ 收敛的较快，准确来说：

$f\left ( \theta +\epsilon \right )\approx f\left ( \theta \right )+\epsilon f{}'{\left ( \theta \right )}+\frac{1}{2}\epsilon ^{2}f{}''\left ( \theta \right )+\frac{1}{6}\epsilon ^{3}f{{}'}''(\theta )+...$

$\frac{f(\theta +\epsilon )-f(\theta )}{\epsilon }\approx f{}'(\theta )+\frac{1}{2}\epsilon f{}''(\theta )$

$\frac{f(\theta +\epsilon )-f(\theta )}{2\epsilon }\approx f{}'(\theta^{} )+\frac{1}{6}\epsilon^{2} f{}'''(\theta )$

当 $lim_{\epsilon ->0}$ 时，上面(2)收敛速度为 $O\left ( \epsilon \right )$ ，(3)式的收敛速度是 $O\left ( \epsilon^{2} \right )$ 。选用(3)式估计导数是一个更好的选择。

我们可以利用上面的公式调试深度学习中的梯度计算。其步骤如下：

1. 把所有参数 $W^{[1]},b^{[1]}...$ reshape 成向量，再把所有向量拼接(concatenate)成一个新向量 $\theta$

2.现在，我们有损失函数 $J\left ( \theta \right )$ 和导数 $d\theta$ 。

3.对于某一个参数 $\theta _{i}$ ，计算其导数估计值：

$\hat{d_{\theta _{i}}}=\frac{J\left ( \theta _{0} \right....,\theta _{i}+\epsilon ... )-J(\theta _{0},...\theta _{i}-\epsilon ...)}{2\epsilon }$

4.比较 $\hat{d_{\theta _{i}}}$ ， ${d_{\theta _{i}}}$ 计算误差值：

5.遍历 $\hat{d_{\theta _{i}}},{d_{\theta _{i}}}$ 计算误差值：

$error =\frac{\left \| \hat{d_{\theta _{i}}}-{d_{\theta _{i}}} \right \|_{2}}{\left \| \hat{d_{\theta _{i}}} \right \|_{2}\cdot \left \| {d_{\theta _{i}}} \right \|_{2}}$

5.遍历所有 $\theta _{i}$ ，做这个检查。

一般可以令 $\epsilon =10^{-7}$ 。如果error在 $10^{-7}$ 这个量级，则说明导数计算得没什么问题。 $10^{-5}$ 可能要注意一下，而 $10^{-3}$ 则大概率说明这里的导数算得有问题。

使用此梯度检查法时，有一些小提示：

不要每次训练的都用，只在训练前调试用。

梯度检查确实很慢，计算复杂度是 $\Omega (\left | \theta \right |^{2})$ （这里没有用大O标记，因为复杂度的下界是那个值，而不是上界）（这个复杂度是 $\left | \theta \right |$ 乘上算一遍推理的运算量得来的。推理至少遍历每个参数一遍，所以推理的复杂度是 $\Omega (\left | \theta \right |)$ ）。

如果梯度检查出现了问题，尝试debug具体出错的参数。
别忘记损失函数中的正则化项。
无法调试 dropout.
有时候，当W，b 过大时导数的计算才会出现较大的误差。可以尝试先训练几轮网络，等参数大了，再做一次梯度检查。

这堂课的信息量十分大。让我们总结一下：

数据集划分
训练集/开发集/测试集的意义
怎么去根据数据规模划分不同的数据集
偏差与方差
如何分辨高偏差与高方差问题
高偏差与高方差问题的一般解决思路
正则化
权重衰减
dropout
数据增强
提前停止
梯度问题
梯度问题的产生原因
缓解梯度问题的方法
梯度检查的实现

这堂课中，正则化和参数带权初始化是两个很重要的话题，展开来的话有很多东西要学。过段时间，我会在课堂内容的基础上，对这些知识进行拓展介绍。

二.改进梯度下降算法（mini-batch, Momentum, Adam)

一直以来，我们都用梯度下降法作为神经网络的优化算法。但是，这个优化算法还有很多的改进空间。在这节课中我们将学习一些更高级的优化技术，希望能够从各个方面改进普通的梯度下降算法。

我们要学习的改进技术有三大项：分批梯度下降、高级更新方法、学习率衰减。这三项是平行的，可以同时使用。

分批梯度下降时从数据集的角度改进梯度下降，我们没必要等遍历完了整个数据集后再进行参数更新，而是可以遍历完一小批数据后就进行更新。

高级更新方法是指不使用参数的梯度值，而是使用一些和梯度相关的中间结果来更新参数，通过使用这些更高级的优化算法，我们能令指令参数更新的更加平滑，更容易收敛到最优值，这些高级的算法包括gradient descent with momentum, RMSProp, Adam。其中Adam是前两种算法的结合版，这是目前最流行的优化器之一。

学习率衰减指的是随着训练的进行，我们可以想办法减小学习率的值，从而减少参数的震荡，令参数更快地靠近最优值。

在这周的课里，我们要更关注每种优化算法的单独、组合使用方法，以及应该在什么场合用什么算法，最后再去关注算法的实现原理。对于多数技术，“会用”一般要优先于“会写”。

2.1分批梯度下降

方法的本质区别是是否把整个数据集分成多个子集。

2.11使用mini-batch

在之前的学习中，我们都是用整个训练集的平均梯度来更新模型参数的。而如果训练集特别大的话，遍历整个数据集要花很长时间，梯度下降的速度将十分缓慢。

其实，我们不一定要等遍历完了整个数据集再做梯度下降。相较于每次遍历完所有个训练样本再更新，我们可以遍历完一小批次(mini-batch)的样本就更新。让我们来看课件里的一个例子：

假设整个数据集大小。我们可以把数据集划分成5000个mini-batch，其中每一个batch包含1000个数据。做梯度下降时，我们每跑完一个batch里的1000个数据，就用它们的平均梯度去更新参数，再去跑下一个batch。

这里要介绍一个新的标记。设整个数据集X的形状是 $\left ( n_{x},m \right )(m=5000,000)$ ，则第i个数据集的标记为 $X^{\left \{ i \right \}}$ ,形状为 $\left ( n_{x},1000 \right )$ 。

使用了分批梯度下降后，算法的写法由

for i in range(m):
    update parameters

变成

for i in range(m / batch_size)
  for j in range(batch_size):
      update parameters

现在的梯度下降法每进行一次内层循环，就更新一次参数。我们还是把一次内层循环称为一个"step（步）"。此外，我们把一次外层循环称为一个"epoch(直译为'时代’，简称‘代’)"，因为每完成一次外层循环就意味着训练集被遍历了一次。

2.12mini-batch的损失函数变化趋势

使用分批梯度下降后，损失函数的变化趋势会有所不同:

如上图所示，如果是使用整批梯度下降，则损失函数会一直下降。但是，使用分批梯度下降后，损失函数可能会时升时降，但总体趋势保持下降。

这种现象主要是因为之前我们计算的是整个训练集的损失函数，而现在计算的是每个mini-batch的损失函数。每个mini-batch的损失函数时高时低，可以理解为：某批数据比较简单，损失函数较低；另一批数据难度较大，损失函数较大。

2.13选择批次大小

批次大小(batch size)对训练速度有很大的影响。

如果批次过大，甚至极端情况下batch_size=m，那么这等价于整批梯度下降。我们刚刚也学过了，如果数据集过大，整批梯度下降是很慢的。

如果批次过小，甚至小到batch_size=1（这种梯度下降法有一个特别的名字：随机梯度下降（Stochastic Gradient Descent）），那么这种计算方法又会失去向量化计算带来的加速效果。

回想一下第二周的内容：向量化计算指的是一次对多个数据做加法、乘法等运算。这种计算方式比用循环对每个数据做计算要快。

出于折中的考虑，我们一般会选用一个介于1-m之间的数作为批次大小。

如果数据集过小(m<2000)，那就没必要使用分批梯度下降，直接拿整个数据集做整批梯度下降即可。

如果数据集再大一点，就可以考虑使用64, 128, 256, 512这些数作为batch_size。这几个数都是2的次幂。由于计算机的硬件容量经常和2的次幂相关，把batch_size恰好设成2的次幂往往能提速。

当然，刚刚也讲了，使用较大batch_size的一个目的是充分利用向量化计算。而向量化计算要求参与运算的数据全部在CPU/GPU内存上。如果设备的内存不够，则设过大的batch_size也没有意义。

2.2 指数加权移动平均

假设我们绘制了某年每日气温的散点图：

假如让你来描述全年气温的趋势，你会怎么描述呢？

作为人类，我们肯定会说：“这一年里，冬天的气温较低。随后气温逐渐升高，在夏天来到最高值。夏天过后，气温又逐渐下降，直至冬天的最低值。”

但是，要让计算机看懂天气的变化趋势，应该怎么办呢？直接拿相邻的天气的差作为趋势可不行。冬天也会出现第二天气温突然升高的情况，夏天也会出现第二天气温突然降低的情况。我们需要一个能够概括一段时间内气温情况的指标。

2.21 移动平均数

一段时间里的值，其实就是几天内多个值的总体情况。多个值的总体情况，可以用平均数表示。严谨地来说，假如这一年有365天，我们用t表示这一年每天的天气，那么：

$t_{i}=\left\{\begin{matrix} value(i)& 1\leqslant i\leq 365 \\0 & \end{matrix}\right.$

我们可以定义一种叫做移动平均数(Moving Averages) 的指标，表示某天及其前几天温度的平均值。比如对于5天移动平均数ma，其定义如下：

$ma_{i}=\frac{t_{i}+t_{i-1}+t_{i-2}+t_{i-3}+t_{i-4}}{5} (1\leqslant i\leqslant 365)$

假如要让计算机依次输出每天的移动平均数，该怎么编写算法呢？我们来看几个移动平均数的例子：

$ma_{5}=\frac{t_{5}+t_{4}+t_{3}+t_{2}+t_{1}}{5}$

$ma_{6}=\frac{t_{6}+t_{5}+t_{4}+t_{3}+t_{2}}{5}$

$ma_{7}=\frac{t_{7}+t_{6}+t_{5}+t_{4}+t_{3}}{5}$

通过观察，我们可以发现， $ma_{6}=ma_{5}+(t_{6}-t_{1})/5$ $ma_{7}=ma_{6}+(t_{7}-t_{2})/5$

也就是说，在算n天里的m天移动平均数（我们刚刚计算的是5天移动平均数）时，我们不用在n次的外层循环里再写一个m次的循环，只需要根据前一天的移动平均数，减一个值加一个值即可。这种依次输出移动平均数的算法如下：

input temperature[0:n]
input m

def get_temperature(i):
    return temperature[i] if i >= 0 and i < n else 0

ma = 0
for i in range(n):
    ma += (get_temperature(i) - get_temperature(i - m)) / m
    ma_i = ma
    output ma_i

这种求移动平均数的方法确实很高效。但是，我们上面这个算法是基于所有温度值一次性给出的情况。假如我们正在算今年每天温度的移动平均数，每天的温度是一天一天给出的，而不是一次性给出的，上面的算法应该怎么修改呢？让我们来看修改后的算法：

input m
temp_i_day_ago = zeros((m))

def update_temperature(t):
    for i in range(m - 1):
        temp_i_day_ago[i+1] = temp_i_day_ago[i]
    temp_i_day_ago[0] = t

ma = 0
for i in range(n):
    input t_i
    update_temperature(t_i)
    ma += (temp_i_day_ago[0] - temp_i_day_ago[m]) / m
    ma_i = ma
    output ma_i

由于我们不能提前知道每天的天气，我们需要一个大小为m的数组temp_i_day_ago记录前几天的天气，以计算m天移动平均数。

上述代码的时间复杂度还是有优化空间的。可以用更好的写法去掉update_temperature里的循环，把计算每天移动平均数的时间复杂度变为 $O(1)$ 。但是，这份代码的空间复杂度是无法优化的。为了算m天移动平均数，我们必须要维护一个长度为m的数组，空间复杂度一定是 $O(m)$ 。

对于一个变量的m移动平均数， $O(m)$ 的空间复杂度还算不大。但假如我们要同时维护l个变量的m移动平均数，整个算法的空间复杂度就是 $O(ml)$ 。在l很大的情况下，m对空间的影响是很大的。哪怕m取5这种很小的数，也意味着要多花4倍的空间去存储额外的数据。空间复杂度里这多出来的这个m是不能接受的。

2.22 指数加权移动平均

作为移动平均数的替代，人们提出了指数加权移动平均数（Exponential Weighted Moving Average） 这种表示一段时期内数据平均值的指标。其计算公式为：

$v_{i}=\beta v_{i-1}+(1-\beta )t_{i}$

这个公式直观上的意义为：一段时间内的平均温度，等于上一段时间的平均温度与当日温度的加权和。

相比普通的移动平均数，指数平均数最大的好处就是减小了空间复杂度。在迭代更新这个新的移动平均数时，我们只需要维护一个当前平均数 $v_{i}$ ，一个当前的温度 $t_{i}$ 即可，空间复杂度为 $O(1)$

让我们进一步理解公式中的参数。把公式展开可得：

$v_{i}=(1-\beta )t_{i} + \beta v_{i-1}$

$v_{i}=(1-\beta )t_{i} +(1-\beta )\beta t_{i-1}+\beta ^{2}v_{i-2}$

$v_{i}=(1-\beta )t_{i} +(1-\beta )\beta t_{i-1}+(1-\beta )\beta ^{2}t_{i-2}+\beta ^{3}v_{i-2}$

从这个式子可以看出，之前数据的权重都在以 $\beta$ 的速度指数衰减。根据 $\left ( 1-\epsilon \right )^{\frac{1}{\epsilon }}\approx \frac{1}{e}$ ，并且我们可以认为一个数到了 $\frac{1}{e}$ 就小到可以忽视了，那么指数平均数表示的就是天内数据的平均情况。比如 $\beta =0.9$ 表示的是10天内的平均数据， $\beta =0.99$ 表示的是100天内的平均数据。

2.23 偏差矫正

指数平均数存在一个问题。在刚刚初始化时，指数平均数的值可能不太正确，请看：

$v_{1}=(1-\beta )t_{1}$

$v_{2}=(1-\beta )\beta t_{1}+(1-\beta )t_{2}$

让我们把每一项前面的权重加起来。对于 $v_{1}$ ，前面的权重和是 $1-\beta$ ；对于，前面的权重和是 $\left ( 1-\beta \right )(1+\beta )$ 。显然，这两个权重和都不为1。而计算平均数时，我们希望所有数据的权重和为1，这样才能反映出数据的真实大小情况。这里出现了权重上的“偏差”.

为了矫正这个偏差，我们应该想办法把权重和矫正为1。观察刚才的算式可以发现，第项的权重和如下：

$w_{i}=(1-\beta )(1+\beta +\beta ^{2}+..+\beta ^{i})$

根据等比数列求和公式，上式化简为：

$w_{i}=(1-\beta )\frac{(1-\beta ^{i})}{(1-\beta )}$

$w_{i}=(1-\beta^{i})$

为了令权重和为1，我们可以令每一项指数平均数都除以这个和，即用下面的式子计算矫正后的指数平均数 $v_{i}{}'$ :

$v'_{i}=\frac{v_{i}}{1-\beta ^{i}}$

但是，在实践中，由于这个和 $1-\beta ^{i}$ 收敛得很快，我们不会特地写代码做这个矫正。

2.3 Momentum

Gradient Descent with Momentum (使用动量的梯度下降) 是一种利用梯度的指数加权移动平均数更新参数的策略。在每次更新学习率时，我们不用本轮梯度的方向作为梯度下降的方向，而是用梯度的指数加权移动平均数作为梯度下降的方向。即对于每个参数，我们用下式做梯度下降：

$V_{dw}=\beta V_{dw}+\left ( 1-\beta \right )dw$

$V_{db}=\beta V_{db}+\left ( 1-\beta \right )db$

$w:=w-\alpha V_{dw}$

$b:=b-\alpha V_{db}$

也就是说，对于每个参数，我们用它的指数平均值代替进行参数的更新。

使用梯度的平均值来更新有什么好处呢？如下图所示

不使用 Momentum 的话，每次参数更新的方向可能变化幅度较大，如上图中的蓝线所示。而使用 Momentum 后，每次参数的更新方向都会在之前的方向上稍作修改，每次的更新方向会更加平缓一点，如上图的红线所示。这样，梯度下降算法可以更快地找到最低点。

在实现时，我们不用去使用偏差矫正。取0.9在大多数情况下都适用，有余力的话这个参数也可以调一下。

2.4 RMSProp 和 Adam

与 Momentum 类似，RMSProp(Root Mean Squared Propagation) 使用了某种移动平均值来平滑梯度的更新。其梯度下降公式如下：

在编程实现时，我们应该给分母加一个极小值，防止分母出现0。

Adam (Adaptive Moment Estimation) 是 Momentum 与 RMSProp 的结合版。为了使用Adam，我们要先计算 Momentum 和 RMSProp 的中间变量：

之后，根据前面的偏差矫正，获得这几个变量的矫正值：

如前文所述，在实现时添加偏差矫正意义不大。估计这里加上偏差矫正是因为原论文加了。

和之前一样，这里的 $\epsilon$ 是一个极小值。在编程时添加，一般都是为了防止分母中出现0。

Adam是目前非常流行的优化算法，它的表现通常都很优秀。为了用好这个优化算法，我们要知道它的超参数该怎么调。在原论文中，这个算法的超参数取值如下：

$\beta _{1}=0.9$

$\beta _{2}=0.999$

$\epsilon =10^{-8}$

绝大多数情况下，我们不用手动调这三个超参数。

2.5 学习率衰减

训练时的学习率不应该是一成不变的。在优化刚开始时，参数离最优值还差很远，选较大的学习率能加快学习速度。但是，经过了一段时间的学习后，参数离最优值已经比较近了。这时，较大的学习率可能会让参数错过最优值。因此，在训练一段时间后，减小学习率往往能够加快网络的收敛速度。这种训练一段时间后减小学习率的方法叫做学习率衰减。

其实学习率衰减只是一种比较宏观的训练策略，并没有绝对正确的学习率衰减方法。我们可以设置初始学习率 $\alpha _{0}$ ，之后按下面的公式进行学习率衰减：

$\alpha =\frac{1}{1+DecayRate*EpochNum}\alpha _{0}$

这个公式非常简单，初始学习率会随着一个衰减率(DecayRate)和训练次数(EpochNum)衰减。

同样，我们还可以使用指数衰减：

$\alpha =0.95^{EpochNum}\alpha _{0}$

或者其他一些奇奇怪怪的衰减方法(k是超参数）：

$\alpha =\frac{k}{\sqrt{EpochNum}}\alpha _{0}$

甚至我们可以手动调学习率，每训练一段时间就把学习率调整成一个更小的常数。

总之，学习率衰减是一条启发性的规则。我们可以有意识地在训练中后期调小学习率。

2.6 局部最优值

在执行梯度下降算法时，局部最优值可能会影响算法的表现：在局部最优值处，各个参数的导数都是0。梯度是0（所有导数为0），意味着梯度下降法将不再更新了。

在待优化参数较少时，陷入局部最优值是一种比较常见的情况。而对于参数量巨大的深度学习项目来说，整个模型陷入局部最优值是一个几乎不可能发生的事情。某参数在梯度为0时，既有可能是局部最优值，也可能是局部最差值。不妨设两种情况的概率都是0.5。如果整个模型都陷入了局部最优值，那么所有参数都得处于局部最优值上。假设我们的深度学习模型有10000个参数，则一个梯度为0的点是局部最优值的概率是 $0.5^{10000}$ ，这是一个几乎不可能发生的事件。

所以，在深度学习中，更常见的梯度为0的点是鞍点（某处梯度为0，但不是局部最值）。在鞍点处，有很多参数都处于局部最差值上，只要稍微对这些参数做一些扰动，参数就会往更小的方向移动。因此，鞍点不会对学习算法产生影响。

在深度学习中，一种会影响学习速度的情况叫做“高原”（plateau）。在高原处，梯度的值一直都很小。只有跨过了这段区域，学习的速度才会快起来。这种情况的可视化结果如下

总而言之，深度学习问题和简单的优化问题不太一样，不用过多担心局部最优值的问题。而高原现象确实会影响学习的速度。

总结

这周，我们围绕深度学习的优化算法，学习了许多提升梯度下降法性能的技术。让我们来捋一捋。

首先，我们可以在处理完一小批数据后就执行梯度下降，而不必等处理完整个数据集后再执行。这种算法叫分批梯度下降（mini-batch gradient descent)。这是一种对梯度下降法的通用改进方法，即默认情况下，这种算法都可以和其他改进方法同时使用。

之后，我们学习了移动平均的概念，知道移动平均值可以更平滑地反映数据在一段时间内的趋势。基于移动平均值，有 gradient descent with momentum 和 RMSProp 这两种梯度下降的改进方法。而现在非常常用的 Adam 优化算法是Momentum 和 RMSProp 的结合版。

最后，我们学习了学习率衰减的一些常见方法。

学完本课的内容后，我认为我们应该对相关知识达到下面的掌握程度：

分批梯度下降
- 了解原理
- 掌握如何选取合适的 batch size
高级优化算法
- 了解移动平均数的思想
- 了解 Adam 的公式
- 记住 Adam 超参数的常见取值
- 未来学习了编程框架后，会调用 Momentum，Adam 优化器
学习率衰减
- 掌握“学习率衰减能加速收敛”这一概念
- 在训练自己的模型时，能够有意识地去调小学习率
局部最优值
- 不用管这个问题

三. 调参、批归一化、多分类任务、编程框架

这周的知识点也十分分散，主要包含四项内容：调参、批归一化、多分类任务、编程框架。

通过在之前的编程项目里调整学习率，我们能够体会到超参数对模型效果的重要影响。实际上，选择超参数不是一个撞运气的过程。我们应该有一套系统的方法来快速找到合适的超参数。

两周前，我们学习了输入归一化。类似地，如果对网络的每一层都使用归一化，也能提升网络的整体表现。这样一种常用的归一化方法叫做批归一化。

之前，我们一直都在讨论二分类问题。而只要稍微修改一下网络结构和激活函数，我们就能把二分类问题的算法拓展到多分类问题上。

为了提升编程的效率，从这周开始，我们要学习深度学习编程框架。编程框架往往能够帮助我们完成求导的功能，我们可以把精力集中在编写模型的正向传播上。

3.1 调参

调参的英文动词叫做tune，这个单词作动词时大部分情况下是指调音。这样一看，把调参叫做“调整参数”或“调试参数”都显得很“粗鲁”。理想情况下，调参应该是一个系统性的过程，就像你去给乐器调音一样。乱调可是行不通的。

3.11 超参数优先级

回顾一下，我们接触过的超参数有：

学习率 $\alpha$
momentum $\beta$
adam $\beta _{1}, \beta _{2},\epsilon$
隐藏层神经元数
层数
学习率递减率
mini-batch size

其中，优先级最高的是学习率。吴恩达老师建议大家调完学习率后，再去调、隐藏层神经元数、mini-batch size。如果使用adam，则它的三个参数基本不用调。

3.12 超参数采样策略

在尝试各种超参数时，不要按“网格”选参数（如下图左半所示），最好随机选参数（如下图右半所示）：

如果用网格采样法的话，你可能试了25组参数，每个参数只试了5个不同的值。而实际上，你试的两个参数中只有一个参数对结果的影响较大，另一个参数几乎不影响结果。最终，你尝试的25次中只有5次是有效的。

而采用随机采样法试参数的话，你能保证每个参数在每次尝试时都取不同值。这样试参数的效率会更高一点。

另外，调参时还有一个“由粗至精”的过程。如下图所示：

当我们发现某几个参数的结果比较优秀时，我们可以缩小搜索范围，仅在这几个参数附近进行搜索。

3.13超参数搜索尺度

搜索参数时，要注意搜索的尺度。如果搜索的尺度不够恰当，我们大部分的调参尝试可能都是无用功。

比如当搜索学习率时，我们应该按0.0001, 0.001, 0.01, 0.1, 1这样指数增长的方式去搜索，而不应该按0.2, 0.4, 0.6, 0.8, 1这种均匀采样的方式搜索。这是因为学习率是以乘法形式参与计算，取0.4, 0.6, 0.8得到的结果可能差不多，按这种方式采样的话，大部分的尝试都是浪费的。而以0.001, 0.01, 0.1这种方式取学习率的话，每次的运行结果就会差距较大，每次尝试都是有意义的。

除了搜索学习率时用到的指数采样，还有其他的采样方式。让我们看调整momentum项的情况。回忆一下， $\beta$ 取0.9，表示近10项的平均数； $\beta$ 取0.99，表示近100项的平均数。也就是说， $\beta$ 表示 $\frac{1}{1-\beta }$ 项的平均数。我们可以对 $\frac{1}{1-\beta }$ 进行指数均匀采样。

当然，有些参数是可以均匀采样的。比如隐藏层的个数，我们可以从[2, 3, 4]里面挑一个；比如每个隐藏层的神经元数，我们也可以直接均匀采样。

总结一下，我们在搜索超参数的时候，应该从超参数所产生的影响出发，考虑应该在哪个指标上均匀采样，再反推超参数的采样公式，而不一定要对超参数本身均匀采样。

当然了，如果我们不确定应该从哪个尺度对超参数采样，可以先默认使用均匀采样。因为我们会遵循由粗至精的搜索原则，尝试几轮后我们就能够观察出超参数的取值规律，从而在正确的尺度上对超参数进行搜索。

3.2 批归一化（Batch Normalization）

在第五篇笔记中，我们曾学习了输入归一化。其计算公式如下：

通过归一化，神经网络第一层的输入更加规整，模型的训练速度能得到有效提升。

我们知道，神经网络的输入可以看成是第零层（输入层）的激活输出。一个很自然的想法是：我们能不能把神经网络每一个隐藏层的激活输出也进行归一化，让神经网络更深的隐藏层也能享受到归一化的加速？

批归一化(Batch Normalization)就是这样一种归一化神经网络每一个隐藏层输出的算法。准确来说，我们归一化的对象不是每一层的激活输出 $a^{[l]}$ ，而是激活前的计算结果 $z^{[l]}$ 。让我们看看对于某一层的激活前输出 $z=z^{[l]}$ ，我们该怎么进行批归一化。

首先，还是先获取符合标准正态分布的归一化结果 $z_{norm}^{(i)}$ ：

我们不希望每一层的输出都固定为标准正态分布，而是希望网络能够自己选择最恰当的分布。因此，我们可以用下式计算最终的批归一化结果：

$\tilde{z}^{(i)}=\gamma z_{norm}^{(i)}+\beta$

其中 $\tilde{z}^{(i)}$ 是最终的批归一化结果， $\gamma \beta$ 都是可学习参数，分别影响新分布的方差与均值。

为什么我们不希望数据的分布总是标准正态分布呢？可以考察一个即将送入sigmoid的 $z\tilde{}$ 。sigmoid在[-1, 1]这段区间内近乎是一个线性函数，为了利用该激活函数的非线性区域，我们应该让z的取值范围更大一点，即让z的方差大于1。

这里的 $\beta$ 和梯度下降算法里的 $\beta$ 不是同一回事，只是这几个算法的原论文里都使用了这个符号。

使用批归一化后，原来的神经网络计算公式需要做出一些调整。之前， $z^{(i)}$ 的计算公式如下：

$z^{(i)} = Wa^{(i)}+b$

现在，我们会把 $z^{(i)}$ 的均值归一化到0。因此，+b成为了一个冗余的操作。使用了批归一化后，应该按下面的方法计算：

$z^{(i)} = Wa^{(i)}$

总结一下，加入批归一化后，神经网络的计算过程如下所示：

$X\rightarrow Z^{[1]}(use W^{[1]})\rightarrow \tilde{Z}^{[1]}(\gamma ^{[1]}*Z_{norm}^{[l]}+\beta ^{[l]})\rightarrow A^{[1]}\rightarrow ...$

注意，使用向量化计算后， $\tilde{Z}^{[l]}=\gamma ^{[l]}*Z_{norm}^{[l]}+\beta ^{[l]}$

其中 $\gamma ^{[l]}$ 和 $\beta ^{[l]}$ 的形状都是 $\left ( n^{[l]},1 \right )$

求导公式：

$d\beta =\frac{1}{m}dA$

$d\gamma =\frac{1}{m}dA*Z_{norm}^{[l]}$

使用批归一化后，常见优化算法（mini-batch, momentum, adam, ...）仍能照常使用。

3.22直观理解批归一化的作用

对于神经网络中较深的层，它们只能“看到”来自上一层的激活输出，而不知道较浅的层的存在。如下图所示，对于第3层，它只知道第2层的激活输出 $A^{[2]}$ 。

这样，经过一段时间的训练后，网络的第3层和第4层知道了如何较好地把 $A^{[2]}$ 映射成 $\tilde{y}$ 。

可是， $A^{[2]}$ 并不是神经网络的真实输入。神经网络真正的结构如下：

$A^{[2]}$ 其实还受到神经网络前2层参数的影响。一旦前2层的参数更新， $A^{[2]}$ 的分布也会随之改变，第3层和第4层可能要从头学习 $A^{[2]}$ 到 $\tilde{y}$ 的映射关系。

与之相比，使用了批归一化后，神经网络每一层的输出都会落在一个类似的分布里。这样，浅层和深层之间就没有那么强的依赖关系，较深的层能够更快完成学习。

顺带一提，当我们用批归一化的同时，如果还使用了mini-batch，则批归一化还能稍微起到一点正则化的作用。这是因为在mini-batch上每层批归一化用到的方差和均值是不准确的，这种“带噪音”的批归一化能够起到和dropout类似的作用，防止神经网络以较大的权重依赖于少数神经元。

3.23测试时的批归一化

我们刚刚学习的批归一化操作，其实都是针对训练而言的。在训练时，我们有大批的数据，可以轻松算出每一层中间结果 $Z^{[l]}$ 的均值和方差。但是，在测试时，我们可能只会对一项输入进行计算。对一项输入计算均值和方差是没有意义的。因此，我们要想办法决定测试时 $Z^{[l]}\rightarrow Z_{norm}^{[l]}$ 用到的均值和方差。

我们可以用每一个mini-batch的均值和方差的指数加权移动平均数作为测试时的均值和方差。

3.3 Softmax 与多分类问题

之前我们一直都在讨论二分类问题。比如，辨别一张图片是不是小猫。当我们把二分类问题拓展到多分类问题时，问题的数学模型会发生哪些变化呢？

首先，我们来看一下多分类问题的定义。在多分类问题中，我们要要判断一个输入是属于C种类型中的哪一种。比如我们希望判断一张图片里的生物是属于小猫、小狗、小鸡、其他这C=4类中的哪一种。

在二分类问题中，我们用1表示“是某一类”，0表示“不是某一类”。我们只需要计算 $P\left ( \tilde{y}=1|x \right )$ 这一个概率。而多分类问题中，我们用一个数字表示一种类别，比如0表示“其他”，1表示“小猫”，2表示“小狗”，3表示“小鸡”。这样，我们就应该计算多个概率，比如这四个概率。

$P\left ( \tilde{y}=0|x \right )$ , $P\left ( \tilde{y}=1|x \right )$ , $P\left ( \tilde{y}=2|x \right )$ , $P\left ( \tilde{y}=3|x \right )$

多分类问题的示意图和一个可能的多分类神经网络如下图所示（注意，该网络有4个输出）：

接着，我们来看看多分类问题带来了哪些新的困难。在二分类问题中，我们得到了最后一层的计算结果 $Z^{[L]}$ ，我们要用sigmoid把它映射到表示概率的[0, 1]上。而多分类问题中，同理，我们要把神经网络最后一层的计算结果 $z^{[L]}$ 映射成一些有实际意义的概率值。具体而言，我们应让所有分类概率之和为1，即 $\sum_{i=1}^{C}P(\tilde{y}=i|x)=1$ 。为了达到这个目的，我们要引入一个激活函数——softmax。

和其他定义在一个实数上的激活函数不同，softmax定义在一个向量上，其计算方式为：

$Input z^{[l]}$

$output a^{[L]}$

$t=e^{z^{{[L]}}}$

$a^{[L]}=\frac{t}{\sum_{i=1}^{C}t_{i}}$

注意，上式中所有运算都是逐元素运算。比如在上面提到的有四个类别的分类问题中， $Z^{[L]}$ 是一个形状为 $\left ( 4,1 \right )$ 的张量，经过逐元素运算后， $t,a^{[L]}$ 都是形状为 $\left ( 4,1 \right )$ 的张量.

为什么要使用向量每个分量的自然指数作为归一化的变量，而不直接对原向量做标准归一化呢？可以考虑[1, 2], [10, 20]这两个向量。如果直接对这两个量进行进行归一化，算出来的概率都是[0.33, 0.67]。而实际上，第一个向量可能对应一幅比较模糊的输入，第二个向量可能对应一幅比较清楚的输入。显然，在更清晰的输入上，我们更有把握说我们的分类结果是正确的。通过使用softmax，我们可以放大数值的影响，[10, 20]相比[1, 2]，我们更有把握说输入是属于第二个类别的。

在C=2时，softmax会退化成sigmoid。也就是说，softmax是sigmoid在多分类任务上的推广。

softmax这个名字，其实衍生自hardmax这个词。使用hardmax时，输入会被映射成[1, 0, 0, 0]这样一个one-hot向量。这种最大值太严格（hard）了，所以有相对来说比较宽松（soft）的最大值计算方法softmax。