二叉树练习题（一）二叉树的遍历

最新推荐文章于 2025-04-14 19:59:12 发布

weixin_41611045

最新推荐文章于 2025-04-14 19:59:12 发布

阅读量1.7w

点赞数 9

分类专栏：算法及数据结构

本文链接：https://blog.csdn.net/weixin_41611045/article/details/102057630

版权

算法及数据结构专栏收录该内容

17 篇文章

订阅专栏

本文详细介绍了二叉树的遍历方法，包括先序、中序、后序及层次遍历，同时探讨了之字形打印和满二叉树判断等高级主题，为读者提供了深入理解二叉树结构的基础。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述
练习题1：如何根据二叉树的遍历结果重置二叉树：
对于先序遍历我们知道，最先出现的一般是根节点，而中序遍历一般将根节点出现在中间，后序遍历将跟节点出现在最后，我们可以根据根节点所在为止划分子树，然后重置二叉树
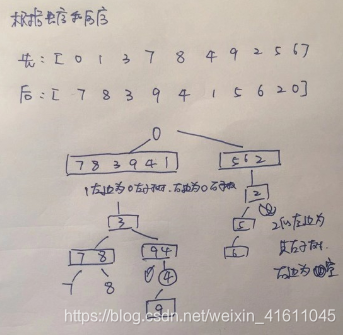
在这里插入图片描述

例题1：对于上述二叉树，请实现层次遍历、先序遍历、中序遍历和后序遍历


'''
二叉树的遍历
将以下二叉树分别用先序遍历、中序遍历、后序遍历和层次遍历进行遍历
      0
   1      2
 3   4   5  6
7 8 9
先序遍历：中左右
中序遍历：左中右
后序遍历：左右中
'''
class TreeNode:
     def __init__(self, x):
         self.val = x
         self.left=None
         self.right=None
#生成二叉树
node_0=TreeNode(0)
node_1=TreeNode(1)
node_2=TreeNode(2)
node_3=TreeNode(3)
node_4=TreeNode(4)
node_5=TreeNode(5)
node_6=TreeNode(6)
node_7=TreeNode(7)
node_8=TreeNode(8)
node_9=TreeNode(9)

node_0.left=node_1
node_0.right=node_2
node_1.left=node_3
node_1.right=node_4
node_2.left=node_5
node_2.right=node_6
node_3.left=node_7
node_3.right=node_8
node_4.left=node_9
#前序遍历
def priosearch(head):
    if head==None:
        return
    print(head.val,end=' ')
    priosearch(head.left)
    priosearch(head.right)
priosearch(node_0)
#0 1 3 7 8 4 9 2 5 6 
#中序遍历
def midsearch(head):
    if head==None:
        return
    midsearch(head.left)
    print(head.val,end=' ')
    midsearch(head.right)
midsearch(node_0)
#7 3 8 1 9 4 0 5 2 6 
#后序遍历
def backsearch(head):
    if head==None:
        return
    backsearch(head.left)
    backsearch(head.right)
    print(head.val,end=' ')
backsearch(node_0)
#层次遍历,利用队列的方式去遍历
def cengcisearch(head):
    arr=[]
    arr.append(head)
    while arr:
        c_root=arr.pop(0)
        print(c_root.val,end=' ')
        if c_root.left is not None:
            arr.append(c_root.left)
        if c_root.right is not None:
            arr.append(c_root.right)
cengcisearch(node_0)            
#0 1 2 3 4 5 6 7 8 9

习题2：剑指offer32
按层打印二叉树，从上到下从左向右
在这里插入图片描述

'''
从上至下层次打印二叉树
如：
        8
   6         10
5    7    9      11
'''
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
Node1=TreeNode(8)
Node2=TreeNode(6)
Node3=TreeNode(10)
Node4=TreeNode(5)
Node5=TreeNode(7)
Node6=TreeNode(9)
Node7=TreeNode(11)
Node1.left=Node2
Node1.right=Node3
Node2.left=Node4
Node2.right=Node5
Node3.left=Node6
Node3.right=Node7

head=Node1
def cenciprint(head):
    if head is None:
        return
    list1=[] #当前节点要打印的元素
    list2=[] #将节点弹出的下一层节点暂时存储的数组
    list1.append(head)
    while list1 or list2:
        while list1:
            c_root=list1.pop(0)
            list2.append(c_root)
        #此时list2已经将这一层节点全部存储了
        while list2:
        #将这一层的节点全部打印，并将当前节点的左右节点放入list1中
            root=list2.pop(0)
            print(root.val,end=' ')
            if root.left is not None:
                list1.append(root.left)
            if root.right is not None:
                list1.append(root.right)
        print('\n')
cenciprint(Node1)

解析：使用两个list来实现，首先放入根节点，将根节点的所有子节点遍历并放入list2,从最开始的元素从list2依次弹出，每次打印这个元素，并将其加入list1,相当于在list1进行出栈并添加子树时，先将子树存储起来以防止不断出栈，这样list2中每次存储的都是每一层的所有元素，当两个list1、list2都为空时代表已经全部遍历结束。
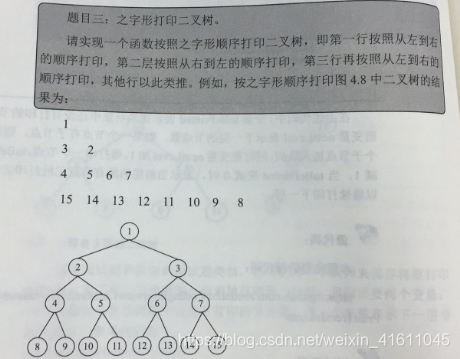
习题3：之字形打印二叉树
在这里插入图片描述

'''
之字形打印二叉树
               1
        2                3
    4      5         6       7
  8   9  10  11    12  13  14  15
打印出来的结果：
1
3 2
4 5 6 7
15 14 13 12 11 10 9 8   
'''
##测试：来回打印
Node1=TreeNode(1)
Node2=TreeNode(2)
Node3=TreeNode(3)
Node4=TreeNode(4)
Node5=TreeNode(5)
Node6=TreeNode(6)
Node7=TreeNode(7)
Node8=TreeNode(8)
Node9=TreeNode(9)
Node10=TreeNode(10)
Node11=TreeNode(11)
Node12=TreeNode(12)
Node13=TreeNode(13)
Node14=TreeNode(14)
Node15=TreeNode(15)
Node16=TreeNode(16)
Node1.left=Node2
Node1.right=Node3
Node2.left=Node4
Node2.right=Node5
Node3.left=Node6
Node3.right=Node7
Node4.left=Node8
Node4.right=Node9
Node5.left=Node10
Node5.right=Node11
Node6.left=Node12
Node6.right=Node13
Node7.left=Node14
Node7.right=Node15
def zhizi_print(head,right_left_triger=False):
    if head is None:
        return
    list1=[] #临时存储下一层节点的值,以队列的形式存储，后面进，前面出
    list2=[] #存储当前节点要打印的值
    list1.append(head)
    while list1 or list2:
        while list1:
            c_root=list1.pop(0)
            list2.append(c_root)         
        while list2:
            if right_left_triger==True:#从右向左打印
                root=list2.pop()
                print(root.val,end=' ')
                if root.right is not None:
                    list1.append(root.right)
                if root.left is not None:
                    list1.append(root.left)
                #此时list1中存储的元素也是从右往左的所以需要将list1颠倒
                #list1=list1[::-1]
            else: #从左向右打印
                root=list2.pop(0)
                print(root.val,end=' ')
                if root.left is not None:
                    list1.append(root.left)
                if root.right is not None:
                    list1.append(root.right)
        #arr=[i.val for i in list1]
        #print(arr)
        if right_left_triger==True:
            right_left_triger=False
            list1=list1[::-1]
        else:
            right_left_triger=True   
        print('\n')
zhizi_print(Node1)

在这里插入图片描述
在上一道每行打印二叉树的基础上进行修改，从左到右和从右到左只需改变list2的弹出顺序，即一个弹出最前面的元素，一个弹出最右边的元素，每次循环完成后改变left的值，如果left时True改为False,如果是False改为True.
习题4：判断二叉树是否为满二叉树
首先完全二叉树树的定义是，加入一个二叉树有h层，除了h层外，其余h-1层均满二叉树状态，第h层所有的节点均从最左边开始生长。