1. 二元函数的极值与驻点
例题
求函数
f
(
x
,
y
)
=
x
3
−
y
3
+
3
x
2
+
3
y
2
−
9
x
f(x,y)=x^3-y^3+3x^2+3y^2-9x
f(x,y)=x3−y3+3x2+3y2−9x的极值：
f
x
(
x
,
y
)
=
3
x
2
+
6
x
−
9
=
0
f_x (x,y)=3x^2+6x-9=0
fx(x,y)=3x2+6x−9=0
f
y
(
x
,
y
)
=
−
3
y
2
+
6
y
=
0
f_y(x,y)=-3y2+6y=0
fy(x,y)=−3y2+6y=0
求得驻点为：(1,0),(1,2),(-3,0),(-3,2)
再求出二阶偏导数
f
x
x
(
x
,
y
)
=
6
x
+
6
f_{xx}(x,y)=6x+6
fxx(x,y)=6x+6
f
x
y
(
x
,
y
)
=
0
f_{xy}(x,y)=0
fxy(x,y)=0
f
y
y
(
x
,
y
)
=
−
6
y
+
6
f_{yy}(x,y)=-6y+6
fyy(x,y)=−6y+6
对各驻点进行判断：
在点（1,0）处，
A
C
−
B
2
=
12
∗
6
>
0
AC-B^2=12*6>0
AC−B2=12∗6>0，又A>0，所以函数在（1,0）处有极大值f(1,0)=-5，
其他以此类推。
二、拉格朗日乘数法及条件极值
例1：
例2：
其实这道题是kkt条件的一个应用。
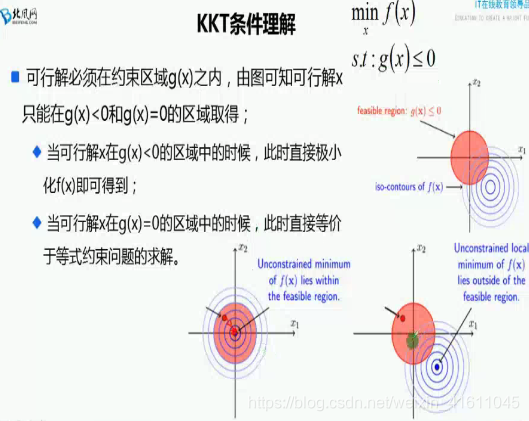
对于不等值约束，我们可以先计算二元函数的一个极值，判断极值是否在限制条件内（即求出来的极值点是否满足限制条件），如果是代表解在限制条件内部直接求极值，如果不是代表点在限制条件外部，则最小值一定是限制条件函数的边缘，此时相当于等值约束。
例2：如果我将限制条件改为
y
>
x
2
且
y
>
=
x
y>x^2且y>=x
y>x2且y>=x此时题目怎么做
高等数学：如何求二元函数的极值问题
最新推荐文章于 2025-02-04 15:33:32 发布
扫一扫
1623
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
