Hyperspectral unmixing阅读笔记---整理中

最近更改了课题，主要在进行Hyperspectral unmixing的研究。 本文会在发布的同时不断更新完善，希望各位看到的朋友帮助我指出错误。文中有很多地方的用词是英文，其原因是笔者是根据英文文献学习，担心不能使用准确的中文名词而导致误解，若有不变还望见谅。

为什么搞Hyperspectral unmixing?

对于Hyperspectral unmixing （HU）的研究，归根结底是源自于Hyperspectral imagery(高光谱， HSI) 的发展。Hyperspectral image 被广泛应用于各个领域，如遥感，农业，矿业等。

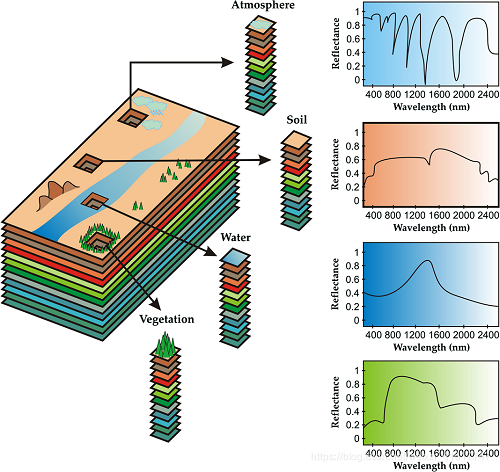
图片来自

在上图中，最左侧的长方体代表着观测到的HSI。HSI 可以同时提供频谱和空间信息，从上图中可以看到HSI 分为许多层，每一个层面都代表着不同光谱下的空间信息。上图中箭头所指即为，从HSI 中选取出不同材质的的光谱特征向量（这一操作成立的前提是后文中描述的pure pixel存在）。但由于HSI 的空间解析度有限， 通常，单个像素可以达到现实中的4m $\times$ 4m到20m $\times$ 20m。因此每一个像素中通常包含多种材料的光谱辐射。为了更好的的实现HSI 分析， Hyperspectral unmixing必不可少。

线性混合模型 Mixture model

前面提到HSI 存在于多种材料信息混合的情况， 为了解决这个问题， 需要建立一个HSI的混合模型以便于进行分解。混合模型可以分为线性混合和非线性混合两种。在实际情况中，非线性更加贴近真实情况，然而线性混合模型（linear mixture model,LMM）虽然简单，但非常具有代表性，许多情况中都可以作为可接受的模型使用。本文所提到的大多数算法都是基于LMM而提出的。 线性模型可以表示为：
$$\mathbf{y}[n]=\sum _{i=1}^N{\mathbf{a}}_i{s}_i[n]+\mathbf{v}[n]=\mathbf{A}\mathbf{s}[n]+\mathbf{v}[n]$$
其中的A矩阵可以称为端元矩阵（endmember matrix)， $y[n]$是位于像素n处的高光谱观测值。${\mathbf{a}}_{\mathbf{i}}$被称为端元特征向量（endmember signature vector）,$s_i[n]$ 表示材料i在像素n处的contribution（贡献值）或proportion（占比），$s[n]$ 被称为丰度向量。 对于丰度向量有着一定的约束，即非负以及和为1：
$$s_i[n]\ge 0,i=1,...,N,and\sum _{i=1}^N{s}_i[n]=1$$
已知观测值$y[n]$, 假设对于端元矩阵$A$我们有充足的信息，并且假设矩阵A为列满秩， 则实现unmixing就可以通过求解LS 问题：
$$\hat{s}[n]=arg\underset{s[n]\in \mathcal{S}}{\min }\Vert y[n]-As[n]{\Vert }_2^{2}z$$
where n = 1,2,…,L

基于LMM的经典解混思路

pure pixel 模型

一种较为特殊的情况是 pure pixel模型。这种情况指某一pixel中的成分只包含一种材料。即：
$$s[l_i]=e_i$$
这里的$e_i$是一个单位向量仅在第$i$处的元素为非零。上式表示，材料$i$在此处所占的比例为1，即该像素处仅包含单一的材料（endmember）。也可以写为：
$$\mathbf{y}[l_{\mathbf{i}}]={\mathbf{a}}_{\mathbf{i}}$$
在Wing-kin Ma的文章中，只要每一个endmember都存在一个pure pixel，就认为该模型是成立的。下文中提出用一个简单的方法实现为所有endmembers寻找他们的pure pixel。

Hyperspectral unmixing algorithm

高光谱的解混算法有很多种，在本节中会分情况讨论不同的算法。

Algorithm for pure pixel

如上文中所提到，不考虑噪声项，并考虑pure pixel假设成立。由于pure pixel 对应的位置并不事先知道，因此一个经典的思路是使用successive projections algrithm(SPA)。有前面的线性混合模型可以得到：
$$\Vert \mathbf{y}[n]{\Vert }_2=\Vert \sum _{i=1}^N{s}_i[n]{\mathbf{a}}_i{\Vert }_2$$
根据三角不等式定理：
$$\Vert \sum _{i=1}^N{s}_i[n]{\mathbf{a}}_i{\Vert }_2\le \sum _{i=1}^N\Vert s_i[n]{\mathbf{a}}_i{\Vert }_2=\sum _{i=1}^N{s}_i[n]\Vert {\mathbf{a}}_i{\Vert }_2$$
由于对于s存在和为一的约束，因此：
$$\sum _{i=1}^N{s}_i[n]\Vert {\mathbf{a}}_i{\Vert }_2\le \underset{i=1,2,...}{\max }\Vert {\mathbf{a}}_{\mathbf{i}}{\Vert }_2$$
上述不等式中的等于情况在$s[n]=e_j$时成立，其中$j=arg{\max }_{i=1,...,N}\Vert {\mathbf{a}}_i{\Vert }_2$，$n=l_j$。即$y[n]$是端元j（the j-th endmember）的pure pixel。
因此可以获得第一个端元特征：
$${\hat{a}}_1=y[{\hat{l}}_i],{\hat{l}}_i=arg\underset{n=1,...,L}{\max }\Vert y[n]{\Vert }_2^2$$
这里的估计值在之前的设定情形下是一个极其完美的$a_1$估计值。
那么如何获得余下的端元的pure pixel？首先假设我们已经获得了$k-1$个端元的特征，分别表示为${\hat{a}}_1,{\hat{a}}_2,...,{\hat{a}}_{k-1}$。使用nulling的方法实现寻找下一个端元。
根据已获得的endmember vector可以获得一个endmember matrix ${\hat{A}}_{1:k-1}=[{\hat{a}}_1,{\hat{a}}_2,...,{\hat{a}}_{k-1}]$。构建一个其对应的orthogonal complement projector $P_{{\hat{A}}_{1:k-1}}^{\perp }$， 在$i<k$时，实现$P_{{\hat{A}}_{1:k-1}}^{\perp }{a}_i=0$。因此我们可以写出：
$$\Vert P_{{\hat{A}}_{1:k-1}}^{\perp }\mathbf{y}[n]{\Vert }_2=\Vert \sum _{i=k}^N{s}_i[n]P_{{\hat{A}}_{1:k-1}}^{\perp }{a}_i{\Vert }_2$$

Convex Geometry（CG）

上述算法基于一种简单的假设，即假设pure pixel成立。实际上pure pixel的理论也是源自于对convex geometry（CG）的学习，可以说是CG 的一种特殊情况。
首先先展示一些较为基础的凸优化表述。
一组向量 { a 1 , . . . , a N } ⊂ R M \{a_1,...,a_N\}\subset \mathbb{R}^M {a1​,...,aN​}⊂RM的 affine hull可以定义为：
a f f { a 1 , a 2 , . . . , a N } = { y = ∑ i = 1 N θ i a i ∣   θ ∈ R … … N , ∑ i = 1 N θ i = 1 } aff\{a_{1},a_{2},...,a_{N}\} = \{y = \sum_{i=1}^{N}\theta_{i}a_{i} |~{\bf{\theta}}\in\mathbb{R}…… {N},\sum_{i=1}^{N}\theta_{i} = 1\} aff{a1​,a2​,...,aN​}={y=i=1∑N​θi​ai​∣ θ∈R……N,i=1∑N​θi​=1}
也可以写做：
a f f { a 1 , a 2 , . . . , a N } = { y = C x + d ∣ x ∈ R P } aff\{a_{1},a_{2},...,a_{N}\} = \{y=Cx+d|x\in \mathbb{R}^{P}\} aff{a1​,a2​,...,aN​}={y=Cx+d∣x∈RP}
一组向量 { a 1 , a 2 , . . . , a N } ⊂ R M \{a_{1},a_{2},...,a_{N}\}\subset \mathbb{R}^{M} {a1​,a2​,...,aN​}⊂RM的convex hull可以定义为：
c o n v { a 1 , a 2 , . . . , a N } = { y = ∑ i = 1 N θ i a i ∣   θ ≥ 0 , ∑ i = 1 N θ i = 1 } conv\{a_{1},a_{2},...,a_{N}\} = \{y = \sum_{i=1}^{N}\theta_{i}a_{i} |~{\bf{\theta}}\geq0,\sum_{i=1}^{N}\theta_{i} = 1\} conv{a1​,a2​,...,aN​}={y=i=1∑N​θi​ai​∣ θ≥0,i=1∑N​θi​=1}
其中 c o n v { a 1 , a 2 , . . . , a N } conv\{a_{1},a_{2},...,a_{N}\} conv{a1​,a2​,...,aN​} 在 { a 1 , a 2 , . . . , a N } \{a_{1},a_{2},...,a_{N}\} {a1​,a2​,...,aN​}映射独立时，可以被称作一个$(N-1)-simplex$。一个simplex的顶点为$a_1,a_2,...,a_N$。 一个满维度的simplex的体积可以描述为：
$$vol(a_1,a_2,...,a_N)=c\left|det\left(\left[\begin{array}{ccc}{a}_1& ...& a_N\\ 1& ...& 1\end{array}\right]\right)\right|=c|det([a_1-a_N,...,a_{N-1}-a_N])|$$
其中$c=1/(N-1)!$.
根据前文提到的线性混合模型， 在不考虑噪音项时，
y [ n ] ∈ c o n v { a 1 , a 2 , . . . , a N } , n = 1 , . . . , L y[n]\in conv\{a_{1},a_{2},...,a_{N}\}, n = 1,...,L y[n]∈conv{a1​,a2​,...,aN​},n=1,...,L
即每一个像素处的观测值$y[n]$都可以表述为i端元特征$a_1,a_2,...,a_N$的凸组合。当N = 3时， c o n v { a 1 , a 2 , . . . , a N } conv\{a_{1},a_{2},...,a_{N}\} conv{a1​,a2​,...,aN​}是一个三角形，每一个$y[n]$都被包含于三角形之中，三角形的顶点是端元特征$a_1,a_2,...,a_N$。因此，如果我们可以找到 c o n v { a 1 , a 2 , . . . , a N } conv\{a_{1},a_{2},...,a_{N}\} conv{a1​,a2​,...,aN​}的每一个顶点，解混就完成了。
上述情况可在下面途中表述出来：
红色三角形区域代表了 c o n v { a 1 , a 2 , . . . , a N } conv\{a_{1},a_{2},...,a_{N}\} conv{a1​,a2​,...,aN​}，三角形中的每一个点都代表着$y[n]$。前面提到，simplex中的每一个点都可以表示为endmember的凸组合。在这种情况下，根据观测值$y[n]$寻找到包围simplex的顶尖，即为解混。

CG based blind HU 直观的来说就是寻找一组向量 { a ^ 1 , a ^ 2 , . . . , a ^ N } \{\hat{a}_{1},\hat{a}_{2},...,\hat{a}_{N}\} {a^1​,a^2​,...,a^N​}， 其对应的simplex c o n v { a ^ 1 , a ^ 2 , . . . , a ^ N } conv\{\hat{a}_{1},\hat{a}_{2},...,\hat{a}_{N}\} conv{a^1​,a^2​,...,a^N​}可以最好的拟合真正的端元simplex c o n v { a 1 , a 2 , . . . , a N } conv\{a_{1},a_{2},...,a_{N}\} conv{a1​,a2​,...,aN​}
当 y [ n ] ∈ c o n v { a ^ 1 , a ^ 2 , . . . , a ^ N } y[n]\in conv\{\hat{a}_{1},\hat{a}_{2},...,\hat{a}_{N}\} y[n]∈conv{a^1​,a^2​,...,a^N​} 时，同样有 y [ n ] ∈ a f f { a ^ 1 , a ^ 2 , . . . , a ^ N } y[n]\in aff\{\hat{a}_{1},\hat{a}_{2},...,\hat{a}_{N}\} y[n]∈aff{a^1​,a^2​,...,a^N​} 成立。因此，$y[n]$同样可以表示为：
$$y[n]=Cx[n]+d$$
这里$C\in {\mathbb{R}}^{M\times (N-1)}$, $rank(C)=N-1$, $d\in {\mathbb{R}}^M$，$x[n]\in {\mathbb{R}}^{N-1}$, $n=1,...,L$。 若$(C,d)$已知，上式可以变形为：
$$x[n]=C^{†}(y[n]-d)$$
根据前文的线性混合模型，可以得到：
$$x[n]=\sum _{i=1}^N{b}_i{s}_i[n]=\mathbf{B}\mathbf{s}[n]$$
这里$b_i=C^{†}(a_i-d)\in {\mathbb{R}}^{N-1},i=1,...,N$, $B=[b_1,...,b_N]\in {\mathbb{R}}^{N-1\times N}$。由维度可见，此处的维度小于原维度$M$，换而言之上述过程实际上实现了降维的功能。

经典的CG思路中有多种方法去解决，例如VOLMAX，N-FINDER，VOLMIN。他们全部建立在对于simplex的估计，并期望达到最佳拟合。希望可以估计出一组合适的 { a ^ 1 . . . a ^ N } \{\hat{a}_1... \hat{a}_N\} {a^1​...a^N​} 可以最大程度的拟合endmember matrix。VOLMAX 和N-FINDER 都是希望在观测值中寻找出可以最大化体积的点，当pure pixel成立时，所得到的simplex即为真正的endmember matrix。然而，Pure pixel的假设往往难以在实际情况中成立，因此SPA、VOLMAX、NFINDR等算法在处理高光谱解混往往难以表现良好。
在诸多文章中，VOLMIN已经被证明可以更好的估算出endmember的位置。其思路是在观测值组外，寻找到可以包含观测值组并有最小体积的simplex。图中对比了在不同观测条件下，三种不同思路的准确度。可以看到当pure pixel成立时，三种算法都可以准确找到真正的endmember（前两种算法正是基于pure pixel假设成立而提出）。而当pure pixel不再成立时，VOLMIN仍能准确定位endmember。但当观测值的分布过于集中时，如图中第三种情况。VOLMIN虽然可以更为接近真正的endmember位置但却不足以准确定位他们的位置。因此上述的算法都存在有一定的局限性。

Nonnegative matrix factorization（NMF）

NMF是一个强有力的工具。NMF的目的是基于观测数据$S\in {\mathbb{R}}^{N\times L}$ 寻找到 $A\in {\mathbb{R}}^{M\times N}$ 和 $S\in {\mathbb{R}}^{N\times L}$ ，其维度满足 N &lt; min ⁡ { M , L } N&lt;\min\{M,L\} N<min{M,L}, 估计两个矩阵的问题可以写为：
$$\underset{A\ge 0,S\ge 0}{\min }\Vert Y-AS{\Vert }_F^2$$

在无源解混的过程中, 矩阵 $A$ 和 $S$ 通常被分别认为是对端元和丰度的估计。然而在使用NMF去实现解混的过程中存在两个问题:

• 过高的计算复杂度，通常被认为是一个NP hard问题
• 简单NMF很难保证其解的唯一性，在HU中也正是一个致命的问题，即其解可能并非真正的端元和丰度

为了解决上述的问题，在使用NMF 解决HU问题时，往往需要对本小节的第一个公式进行补充调整，使其可以更好的符合问题的需求。
$$\underset{A\ge 0,S\ge 0}{\min }\Vert Y-AS{\Vert }_F^2+\alpha \cdot g(A)+\beta \cdot f(S)$$
其中 S L = { S ∣ s [ n ] ≥ 0 , 1 T s [ n ] = 1 , 1 ≤ n ≤ L S^{L} = \{S|s[n]\geq0,1^{T}s[n] = 1,1\leq n\leq L SL={S∣s[n]≥0,1Ts[n]=1,1≤n≤L, $g$ 和 $h$看作 regularizers, $\alpha ,\beta >0$是常数。 regularizers的选择往往根据实际应用算法的不同而更改。
以MVCNMF方法为例，regularizers的选择是simplex的体积。
为了在HU问题中使用NMF并使其拥有唯一解，很多限定条件需要附加到计算中，一方面增加了问题的复杂度，另一方面也使得问题的描述不直观。而HSI往往是以一个三维度tensor提供的，因此使用tensor来描述和解决问题似乎是一种更为直观的方法。

Nonnegative tensor factorization

本小节中会简单介绍四种不同的张量分解思路，此处借用了熊伏枥的博客http://www.xiongfuli.com/中的部分图片：

• CPD

• 

• Tucker decomposition
  

• BTD

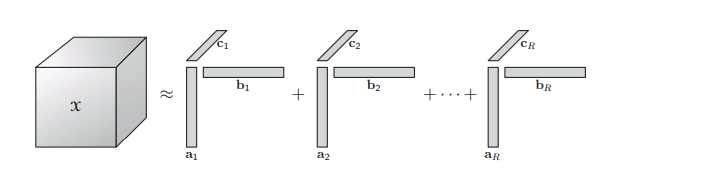
• Matrix-vector tensor decomposition（LL1 BTD）

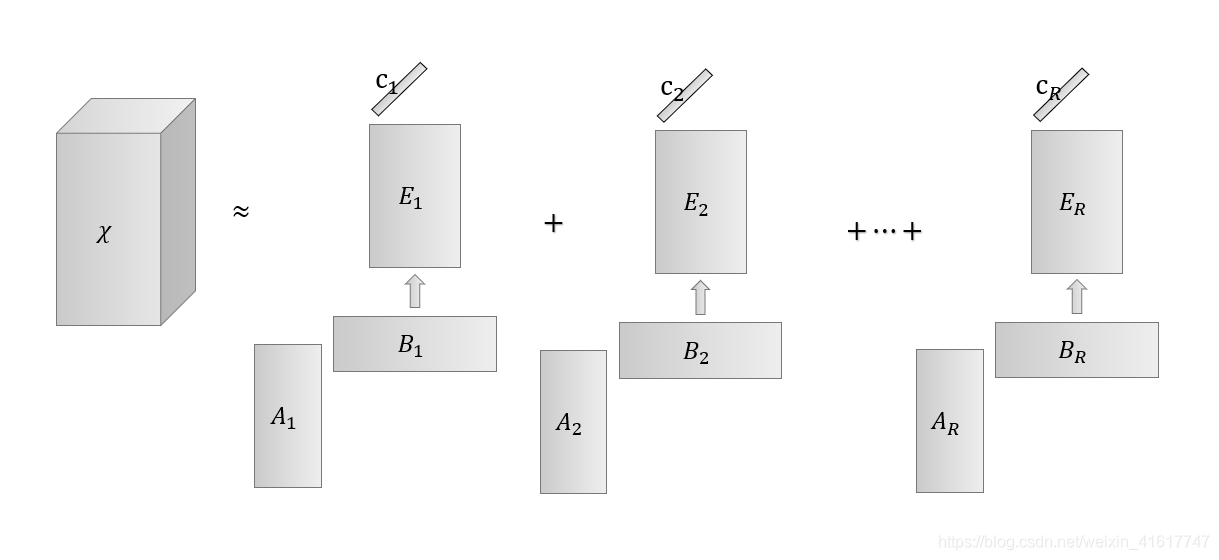
上面四张图片展示了四种不同的tensor展开形式。

相对于NMF，NTF有更为优势的条件去实现 Hyperspectral Unmixing。---------------未完