【花雕学编程】Arduino BLDC 之卡尔曼滤波实现数据融合

《Arduino 手册（思路与案例）》栏目介绍：
在电子制作与智能控制的应用领域，本栏目涵盖了丰富的内容，包括但不限于以下主题：Arduino BLDC、Arduino CNC、Arduino E-Ink、Arduino ESP32 SPP、Arduino FreeRTOS、Arduino FOC、Arduino GRBL、Arduino HTTP、Arduino HUB75、Arduino IoT Cloud、Arduino JSON、Arduino LCD、Arduino OLED、Arduino LVGL、Arduino PID、Arduino TFT，以及Arduino智能家居、智慧交通、月球基地、智慧校园和智慧农业等多个方面与领域。不仅探讨了这些技术的基础知识和应用领域，还提供了众多具体的参考案例，帮助读者更好地理解和运用Arduino平台进行创新项目。目前，本栏目已有近4000篇相关博客，旨在为广大电子爱好者和开发者提供全面的学习资源与实践指导。通过这些丰富的案例和思路，读者可以获取灵感，推动自己的创作与开发进程。
https://blog.csdn.net/weixin_41659040/category_12422453.html

Arduino BLDC之卡尔曼滤波实现数据融合

一、主要特点
数据融合能力：

卡尔曼滤波器能够有效融合来自多个传感器的数据（如IMU、速度传感器等），提供更为准确和可靠的状态估计。这种能力使得系统能够在存在噪声和不确定性的情况下，获得更为精确的信息。
实时性：

卡尔曼滤波器是一种递归滤波器，能够在实时系统中快速更新状态估计，适合动态变化的环境。这使得其在运动控制和导航等需要快速反应的应用中表现出色。
适应性与鲁棒性：

卡尔曼滤波器能够自动调整其估计和误差协方差，适应不同的环境和工作条件。这种鲁棒性使得其在多变的环境中依然能够保持良好的性能。
最优估计：

在高斯噪声条件下，卡尔曼滤波器提供的是最佳线性无偏估计（BLUE），确保在统计意义上获得最优的状态估计。

二、应用场景
机器人导航：

在移动机器人中，卡尔曼滤波器常用于融合IMU和GPS数据，以提高定位精度和导航效果，确保机器人能够在复杂环境中自主移动。
无人驾驶：

在无人驾驶汽车中，卡尔曼滤波器用于融合来自激光雷达、摄像头和IMU的数据，实现精确的环境感知和路径规划。
飞行控制：

在无人机和飞行器中，卡尔曼滤波器被广泛应用于姿态估计和位置跟踪，确保飞行的稳定性和安全性。
运动捕捉：

在运动捕捉系统中，卡尔曼滤波器用于融合多个传感器的数据，提供精确的运动轨迹和姿态信息。

三、注意事项
模型准确性：

卡尔曼滤波器的性能依赖于系统模型和噪声特性的准确性，模型的不准确可能导致估计结果的偏差。因此，在设计滤波器时需要对系统进行充分的建模和验证。
初始条件设定：

滤波器的初始状态和协方差矩阵设置对最终结果有重要影响，不恰当的初始条件可能导致滤波器收敛缓慢或发散。
计算复杂性：

尽管卡尔曼滤波器相对高效，但在处理高维状态空间时，计算复杂性可能会增加，需确保Arduino系统具有足够的计算能力。
噪声特性：

确保对各个传感器的噪声特性进行分析，以合理设定过程噪声和测量噪声的协方差矩阵，这是影响滤波器性能的关键因素。
参数调节：

在实际应用中，卡尔曼滤波器的参数（如协方差矩阵）可能需要根据实际情况进行调节，以达到最佳效果。

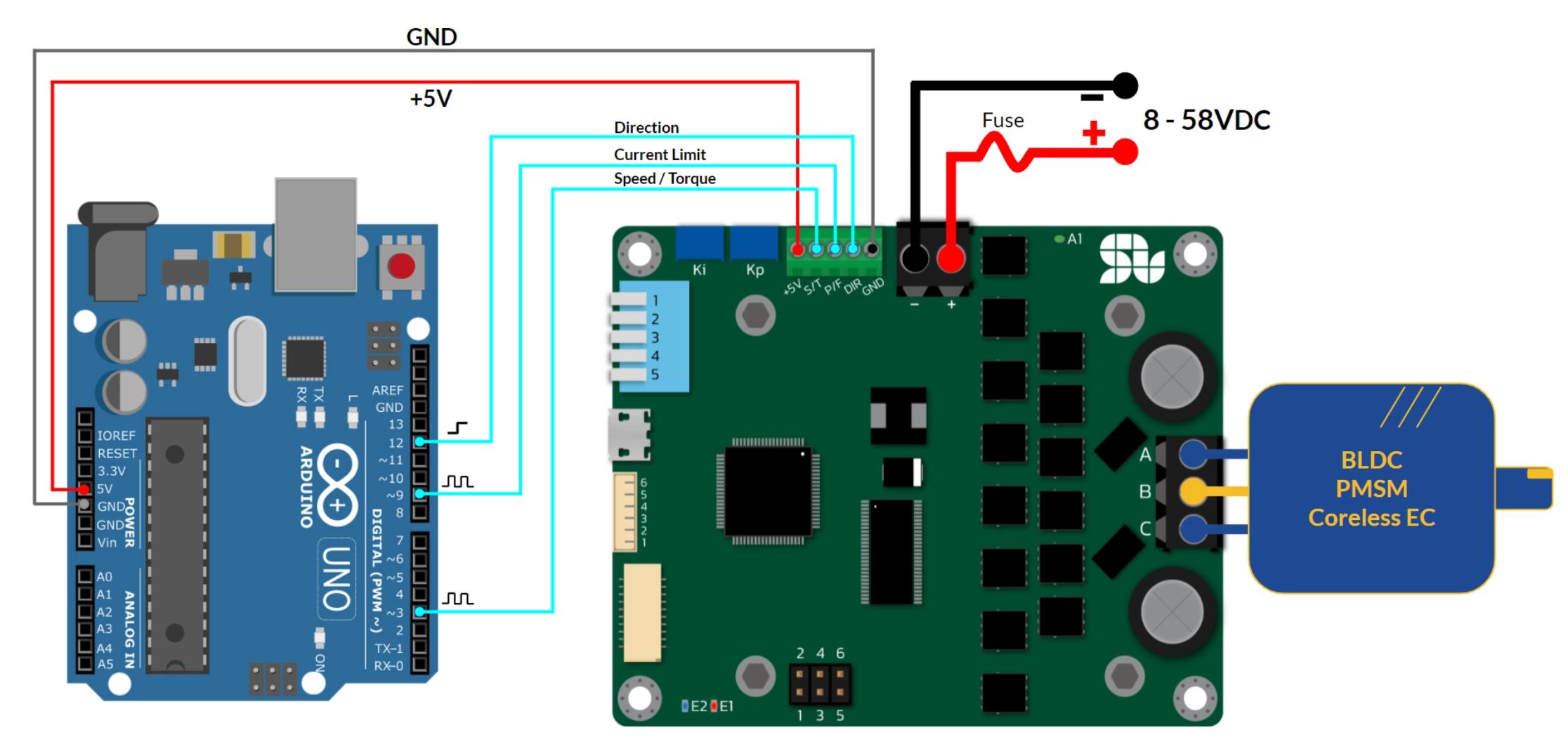
1、基本卡尔曼滤波实现

// 卡尔曼滤波参数
double Q = 0.01; // 过程噪声协方差
double R = 0.1; // 测量噪声协方差
double x_est = 0; // 估计值
double P = 1; // 估计误差协方差

void setup() {
  Serial.begin(9600);
}

void loop() {
  double measurement = analogRead(A0) / 4; // 模拟读取传感器值（0-255）

  // 卡尔曼滤波更新
  // 预测步骤
  P = P + Q;

  // 更新步骤
  double K = P / (P + R); // 卡尔曼增益
  x_est = x_est + K * (measurement - x_est); // 更新估计值
  P = (1 - K) * P; // 更新估计误差协方差

  Serial.print("Measured: ");
  Serial.print(measurement);
  Serial.print(" Estimated: ");
  Serial.println(x_est);

  delay(100);
}

要点解读：
基本卡尔曼滤波：实现了简单的卡尔曼滤波器用于传感器数据的融合，适合初学者理解卡尔曼滤波的基本原理。
实时输出：每次循环中输出测量值和估计值，有助于监控滤波效果。
简单易懂：代码结构清晰，便于学习和扩展。

2、加速度与速度的卡尔曼滤波融合

// 卡尔曼滤波参数
double Q = 0.01; // 过程噪声协方差
double R = 0.1; // 测量噪声协方差
double x_est = 0; // 估计值
double P = 1; // 估计误差协方差

void setup() {
  Serial.begin(9600);
}

void loop() {
  double acceleration = analogRead(A0) / 4; // 模拟读取加速度传感器值（0-255）
  double velocity = x_est; // 将上一次估计值作为当前速度

  // 卡尔曼滤波更新
  // 预测步骤
  velocity += acceleration * 0.1; // 假设时间间隔为0.1秒
  P += Q;

  // 更新步骤
  double K = P / (P + R); // 卡尔曼增益
  x_est = velocity + K * (acceleration - velocity); // 更新估计值
  P = (1 - K) * P; // 更新估计误差协方差

  Serial.print("Acceleration: ");
  Serial.print(acceleration);
  Serial.print(" Estimated Velocity: ");
  Serial.println(x_est);

  delay(100);
}

要点解读：
加速度与速度融合：通过卡尔曼滤波将加速度与计算出的速度进行融合，提高了速度估计的精度。
动态调整：实时更新估计的速度，适应不同的加速度变化。
适用于运动控制：适合需要实时速度反馈的应用，如机器人和电动车。

3、传感器数据融合：陀螺仪与加速度计

// 卡尔曼滤波参数
double Q_angle = 0.01; // 过程噪声协方差
double Q_bias = 0.003; // 角速度的过程噪声
double R_angle = 0.1; // 测量噪声协方差

double angle = 0; // 姿态角度估计
double bias = 0; // 角速度偏差
double rate = 0; // 角速度

void setup() {
  Serial.begin(9600);
}

void loop() {
  double accel_angle = analogRead(A0) / 4; // 模拟读取加速度计值（0-255）
  rate = analogRead(A1) / 4; // 模拟读取陀螺仪值（0-255）

  // 卡尔曼滤波更新
  // 预测步骤
  angle += (rate - bias) * 0.1; // 假设时间间隔为0.1秒
  double P[2][2] = {{1, 0}, {0, 1}};
  P[0][0] += Q_angle;
  P[1][1] += Q_bias;

  // 更新步骤
  double K[2]; // 卡尔曼增益
  double y = accel_angle - angle; // 角度测量误差
  double S = P[0][0] + R_angle;
  K[0] = P[0][0] / S;
  K[1] = P[1][0] / S;

  // 更新估计值
  angle += K[0] * y;
  bias += K[1] * y;
  
  // 更新协方差
  double P00_temp = P[0][0];
  P[0][0] -= K[0] * P00_temp;
  P[0][1] -= K[0] * P[0][1];
  P[1][0] -= K[1] * P00_temp;
  P[1][1] -= K[1] * P[1][0];

  Serial.print("Estimated Angle: ");
  Serial.println(angle);

  delay(100);
}

要点解读：
传感器数据融合：结合加速度计与陀螺仪数据进行姿态估计，适合需要高精度姿态控制的应用。
动态滤波：实时更新角度及偏差，增强了控制系统的稳定性和响应速度。
适用于复杂应用：适合需要准确姿态反馈的设备，如无人机和机器人。

4、BLDC电机速度估计（编码器+电流传感器融合）

#include <SimpleKalmanFilter.h>
#include <Encoder.h>
 
// 传感器配置
Encoder encoder(2, 3);
const int currentPin = A0;
SimpleKalmanFilter kf(2, 2, 0.1);  // 过程噪声Q=2, 测量噪声R=2, 协方差P=0.1
 
// 电机参数
float gear_ratio = 50.0;  // 减速比
float last_position = 0;
unsigned long last_time = 0;
 
void setup() {
  Serial.begin(115200);
  last_time = micros();
}
 
void loop() {
  // 1. 读取编码器位置
  long new_position = encoder.read();
  unsigned long now = micros();
  float dt = (now - last_time) / 1e6;  // 时间间隔（秒）
  
  // 2. 编码器速度计算（机械速度）
  float encoder_speed = ((float)(new_position - last_position) / gear_ratio) / dt * 60.0; // RPM
  last_position = new_position;
  last_time = now;
 
  // 3. 电流传感器速度估计（简化模型：电流与速度近似线性）
  float current = analogRead(currentPin) * 5.0 / 1023.0;  // 电流采样（假设5V对应10A）
  float current_speed = (current - 2.5) * 100.0;  // 偏移2.5V，比例系数100RPM/A
 
  // 4. 卡尔曼滤波融合
  float estimated_speed = kf.updateEstimate(encoder_speed, current_speed);
 
  // 输出结果
  Serial.print("编码器速度: "); Serial.print(encoder_speed);
  Serial.print(" 电流估计速度: "); Serial.print(current_speed);
  Serial.print(" 融合速度: "); Serial.println(estimated_speed);
  delay(10);
}

要点解读：
双传感器冗余：编码器提供高精度速度，电流传感器在编码器失效时提供估计。
卡尔曼参数调优：
增大Q（过程噪声）可加快滤波器对突变响应。
减小R（测量噪声）增加编码器数据的权重。
简化模型假设：电流与速度的线性关系需通过实验标定。

5、无人机云台姿态估计（IMU+编码器融合）

#include <Wire.h>
#include <MPU6050.h>
#include <SimpleKalmanFilter.h>
 
MPU6050 mpu;
Encoder encoder(2, 3);
SimpleKalmanFilter kf_angle(0.1, 0.5, 0.01);  // 角度融合
SimpleKalmanFilter kf_rate(0.05, 0.3, 0.01);  // 角速度融合
 
float last_encoder_angle = 0;
unsigned long last_update = 0;
 
void setup() {
  Serial.begin(115200);
  Wire.begin();
  mpu.initialize();
  mpu.setFullScaleGyroRange(MPU6050_GYRO_FS_250);
  last_encoder_angle = encoder.read() / 1000.0;  // 假设编码器每转1000脉冲
}
 
void loop() {
  unsigned long now = millis();
  float dt = (now - last_update) / 1000.0;
  last_update = now;
 
  // 1. 读取IMU数据
  Vector accel = mpu.readNormalizeAccel();
  Vector gyro = mpu.readNormalizeGyro();
  float accel_angle = atan2(accel.YAxis, accel.ZAxis) * 180 / PI;  // 加速度计角度
  float gyro_rate = gyro.XAxis;  // 陀螺仪角速度（deg/s）
 
  // 2. 读取编码器角度
  float encoder_angle = encoder.read() / 1000.0;
  float encoder_rate = (encoder_angle - last_encoder_angle) / dt;
  last_encoder_angle = encoder_angle;
 
  // 3. 卡尔曼滤波融合
  // 角度融合：优先使用编码器（低噪声），IMU辅助动态响应
  float estimated_angle = kf_angle.updateEstimate(encoder_angle, accel_angle);
  
  // 角速度融合：优先使用陀螺仪（高频响应），编码器校准漂移
  float estimated_rate = kf_rate.updateEstimate(gyro_rate, encoder_rate);
 
  // 输出结果
  Serial.print("编码器角度: "); Serial.print(encoder_angle);
  Serial.print(" IMU角度: "); Serial.print(accel_angle);
  Serial.print(" 融合角度: "); Serial.println(estimated_angle);
  delay(10);
}

要点解读：
多速率采样：IMU通常需要高频采样（如100Hz），编码器采样率较低（如50Hz），需处理时间同步。
噪声特性：
加速度计低频特性好但易受振动干扰（高R值）。
陀螺仪高频响应好但有累积误差（中Q值）。
扩展应用：可加入磁力计实现航向角估计，构建9轴融合系统。

6、移动机器人定位（里程计+IMU融合）

#include <SimpleKalmanFilter.h>
#include <Encoder.h>
#include <MPU6050.h>
 
// 传感器配置
Encoder wheel_left(2, 3);
Encoder wheel_right(4, 5);
MPU6050 mpu;
SimpleKalmanFilter kf_x(0.5, 1.0, 0.1);  // X轴位置
SimpleKalmanFilter kf_y(0.5, 1.0, 0.1);  // Y轴位置
SimpleKalmanFilter kf_theta(0.1, 0.3, 0.01);  // 航向角
 
// 机器人参数
float wheel_radius = 0.05;  // 轮径（米）
float baseline = 0.3;       // 两轮间距（米）
float last_left = 0, last_right = 0;
float x = 0, y = 0, theta = 0;
unsigned long last_time = 0;
 
void setup() {
  Serial.begin(115200);
  Wire.begin();
  mpu.initialize();
  last_time = millis();
}
 
void loop() {
  unsigned long now = millis();
  float dt = (now - last_time) / 1000.0;
  last_time = now;
 
  // 1. 读取编码器数据
  float left_pos = wheel_left.read();
  float right_pos = wheel_right.read();
  float delta_left = left_pos - last_left;
  float delta_right = right_pos - last_right;
  last_left = left_pos;
  last_right = right_pos;
 
  // 2. 里程计计算
  float distance_left = delta_left * 2 * PI * wheel_radius / 1000.0;  // 假设每转1000脉冲
  float distance_right = delta_right * 2 * PI * wheel_radius / 1000.0;
  float delta_distance = (distance_left + distance_right) / 2;
  float delta_theta = (distance_right - distance_left) / baseline;
 
  // 3. IMU航向角
  Vector gyro = mpu.readNormalizeGyro();
  float imu_theta = theta + gyro.ZAxis * dt;  // 简单积分（实际需更复杂处理）
 
  // 4. 卡尔曼滤波融合
  // 位置更新（假设直线运动简化模型）
  x += delta_distance * cos(theta);
  y += delta_distance * sin(theta);
  theta += delta_theta;
 
  // 融合航向角（优先IMU高频数据，里程计校准累积误差）
  theta = kf_theta.updateEstimate(theta, imu_theta);
 
  // 输出结果
  Serial.print("里程计位置: ("); Serial.print(x); Serial.print(", "); Serial.print(y);
  Serial.print(") 融合航向角: "); Serial.println(theta);
  delay(50);
}

要点解读：
运动模型简化：假设小车为差速驱动模型，实际需考虑侧滑等非线性因素。
时间同步：里程计和IMU采样时间可能不同步，需插值处理。
误差累积：里程计在打滑时失效，IMU在长时间运行后有累积误差，卡尔曼滤波可平衡两者。

注意，以上案例只是为了拓展思路，仅供参考。它们可能有错误、不适用或者无法编译。您的硬件平台、使用场景和Arduino版本可能影响使用方法的选择。实际编程时，您要根据自己的硬件配置、使用场景和具体需求进行调整，并多次实际测试。您还要正确连接硬件，了解所用传感器和设备的规范和特性。涉及硬件操作的代码，您要在使用前确认引脚和电平等参数的正确性和安全性。