线性回归
线性回归属于回归问题。对于回归问题,解决流程为:
给定数据集中每个样本及其正确答案,选择一个模型函数h(hypothesis,假设),并为h找到适应数据的(未必是全局)最优解,即找出最优解下的h的参数。这里给定的数据集取名叫训练集(Training Set)。不能所有数据都拿来训练,要留一部分验证模型好不好使,这点以后说。先列举几个几个典型的模型:
多项式回归(Polynomial Regression):
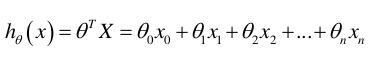
代价函数
计算建立的模型对真实数据的误差,叫建模误差(Modeling Error)。误差越低,模型对数据拟合度越高。例如给出:
m:训练集的样本个数
n:训练集的特征个数(通常每行数据为一个x(0)=1与n个x(i) (i from 1 to n)构成,所以一般都会将x最左侧加一列“1”,变成n+1个特征)
x:训练集(可含有任意多个特征,二维矩阵,行数m,列数n+1,即x0=1与原训练集结合)
y:训练集对应的正确答案(m维向量,也就是长度为m的一维数组)
h(x):我们确定的模型对应的函数(返回m维向量)
theta:h的初始参数(常为随机生成。n+1维向量)
得代价函数J(theta):
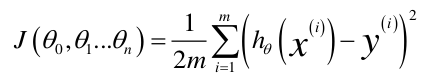
有了代价函数,我们的目的就是找到一组参数theta使得代价最小。
求解代价函数最小值的方法
1、正规方程
我们先回顾一下,我们定义观测结果y和预测结果y'之间的差别为
设若参数的矩阵为,则
那么
按照我们的定义,这个Rss的意思是y和y'之间的差,那么当Rss无限趋近于0的时候,则y≈y',即我们求得的预测结果就等于实际结果。
于是,令Rss等于某一极小值,则
对参数求导,得:
展开,得
进而就可以得到
于是我们就得到正规方程了。
当然很显然的是,如果矩阵不可逆就不能用这个方案了(出现这个情况的原因可能是1.各个特征不独立、有关联,比如出现了重量和质量两个特征(至少在同一个地方两者完全成比例);2.特征数量大于所给训练集样本个数)。
2、批量梯度下降算法
上述方法简单易使用但是局限高,而梯度下降算法使用更广泛更通用。
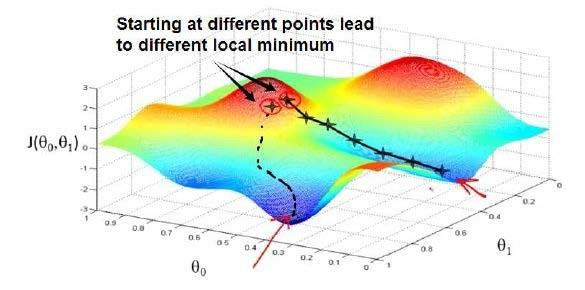
先定下一组预设参数,通常可以是随机生成的,不断微调h的参数直到达到代价J的局部最小值(Local Minimum)。因此此算法并不一定能找到全局最小值(Global Minimum)。根据初始theta选择的不同可能找到不同局部最小值、导致不同结果。下图很形象的表现了这一点。
具体实现:我们循环以下算法直到到达局部最小值。
- alpha是学习率(Learning Rate),其大小决定了每次循环中theta改变的大小,决定了梯度下降步子迈多大。寻找alpha很关键。alpha小了,每次循环步子也迈的小,要很多步才能到达最低点,速度慢。alpha太大了,可能一下就迈过头了,越过了最低点,并不断一次次越过来越过去就是下不来,太大了甚至可能导致循环无法收敛、甚至发散。
可以看出,随着算法越来越接近局部最小值,J’越小,下降速度越慢,因此alpha只需是个定值,无需在靠近最小值时一起减小alpha。
注意,每个theta i必须是同步变换,即不能修改了theta1为新计算得的值后再计算要修改的theta2,这样计算出的theta2是基于是修改后的theta1而得到的。因此要计算出全部新theta后统一赋值。
该梯度下降算法有时也被称为批量梯度下降。“批量”指的是在梯度下降的每一步中,我们都用到了所有的训练样本。
按照梯度下降要求求得代价方程J的导数J’(为了方便书写记J的导数为J’),而对于线性回归模型的J方程上面已经给出,所以将J求导带入,得到:
将求导部分求出来,即:
3、随机梯度下降算法
普通的梯度下降算法更新一次theta需要载入所有样本,也就是说一次更新的计算量为m*n^2(m为样本数量,n为参数数量)。这样如果m 非常大,我们需要把所有样本都载入,才能更新一次参数theta,更新一次theta的时间太久了。
而随机梯度下降算法是每次只取一个样本,马上就更新theta。
也就是说,每次更新theta的计算量为n^2,当m很大的时候,随机梯度下降迭代一次的速度要远高于梯度下降。
当然有弊有利,利就是更新速度很快,弊就是梯度下降的方向不稳。虽然大致方向上还是向着最低点的,但是一路上都在来回移动。要知道毕竟一套参数不能完全满足所有样本,而每个样本都试图将参数向自己方向靠。(说起来这样不应该很可能没法收敛吗?最后会不会一直在最优解附近游荡。) 
需要注意的地方
特征缩放
以房价为例子,现在假设房子价格只受房屋的尺寸(对应theta1)和房间的数量(theta2)影响,房子尺寸的值为 0-2000 平方英尺,而房间数量的值是 0-5,以两个参数为横纵坐标绘图,可以看出图像很扁,梯度下降算法需要非常多次迭代才能收敛。
具体为什么会导致迭代很多次,老师的解释是根据图来的,虽然很直观但是根本原因他没说清楚,现在分析下来我认为原因在于,梯度下降时,alpha对于每个参数都是一样的(现在假定alpha为1),则根据最终得到的算法(“Repeat”里面那行),alpha、1/m、h(xi)-y(i)都是一样的,不一样的只有xj(i)(上标下标不会打,凑合着看),那么对于房屋尺寸,尺寸都上千了,数值很大,则theta1的变化也很大,因此对于theta1,alpha太大了,看那张草图,已经导致了越过最小值的情况。而对于theta2呢,房间一共不会超过5,因此对于theta2,alpha太小了,每次就靠近最小值一点点。
这时候我们就需要特征缩放,把所有参数缩放到-1~1的范围,让alpha适应每个参数,每个参数每次的变化都相当。
具体实施就是令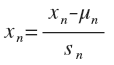
其中u是平均值,s是标准差。把每个数据都如上修改范围,相当于预处理,这样可以对后面线性回归有帮助。而对于多项式回归模型,在运行梯度下降算法前,特征缩放就显得更有必要了。
其实我个人觉得给每个参数分配一个alpha也是可行的一种方案,不过仔细想想,这样的确实麻烦了点,因为找出合适的alpha不是那么容易的事情。
学习率alpha的选择
上面说到了,alpha太大,步子大了容易扯到蛋,可能导致越过最小值甚至无法收敛;alpha小了又显得娘炮,太慢了。
通常可以考虑尝试这些学习率:α=0.01,0.03,0.1,0.3,1,3,10,多试一试找出比较好的。
局部最优解还是全局最优解
之前也明确说了,梯度下降不一定能获得全局最优解,但是网上那么多教程、博客还是写的很混乱,或者说非常不严谨,都说“到达全局最小值”;包括在吴恩达老师的视频里,也不是描述的很清爽。搞得我很懵。所以问题是,梯度下降用来求最优解,哪些问题可以求得全局最优?哪些问题可能获得局部最优解?
如果函数图像只有一个凹坑,像吴大大视频里的例子全都是一个峰的,那梯度下降最终求得的肯定是全局最优解,应该说获得的局部最优解就是全局最优解。然而对于有多个凹坑的问题,梯度下降获得的局部最优解很有可能的最终结果不是全局最优。对于线性回归问题这也是一样的,网上看到有人说线性回归问题只有一个全局最小值没有局部最小值,感觉这不对,我记得吴恩达老师有说过线性回归也可以有极小值存在的。先mark,等我验证后更新。
但是正规方程呢?当有多个极小值时他一定会返回最小值吗?这点我也不清楚,但是按照周志华老师的机器学习的书上说,当特征数量大于所给训练集样本个数时使用正规方程,会得到多个解,而具体返回哪个解就看算法的选择了。
上述方法的问题就是会产生过拟合
过拟合问题及其解决方法
- 问题:以下面一张图片展示过拟合问题
- 解决方法:(1):丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现;(2):使用正则化技术,保留所有特征,但是减少特征前面的参数θ的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
岭回归与Lasso回归
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的,具体三者的损失函数对比见下图:
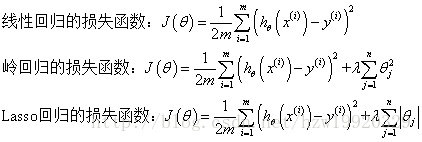
其中λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当,因此λ的选取是一个技术活。岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项,Lasso回归能够使得损失函数中的许多θ均变成0,这点要优于岭回归,因为岭回归是要所有的θ均存在的,这样计算量Lasso回归将远远小于岭回归。
两者的计算代价函数最小值同线性回归模型方法相同
如图所示,为Ridge回归的批量梯度下降法,Lasso同理








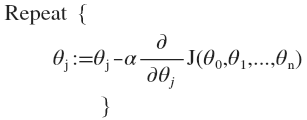
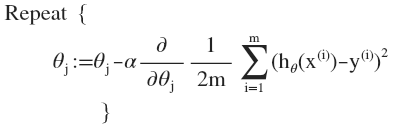


















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








