机器学习流程、有监督学习、无监督学习、数据预处理、特征工程

机器学习流程、有监督学习、无监督学习、数据预处理、特征工程

总共分为四个ipynp文件，主要讲解机器学习的流程，有监督无监督学习，数据处理与特征工程。

1.背景

在我们学习某个行业之前，首先大概了解一下这个行业的发展，以及要研究的方向，以下是从网上找的一些有关于机器学习的一些发展史。

1.1 机器学习40年发展史

1.2 机器学习的前世今生

1.3 一文让你了解机器学习的历史和真谛

2.机器学习综述

经典定义：利用经验改善自身的性能。从过去的大量数据中”总结“出来”泛化规律“的能力，用于新数据预测。从分类上大体可以分为3类。

2.1 监督学习

使用预定义的“训练示例”集合，训练系统，便于其在新数据被馈送时也能得出结论。系统一直被训练，直到达到所需的精度水平。

定义：指有求知欲的学生从老师那里获取知识、信息，老师提供对错指示、告知最终答案的学习过程。 在机器学习中，计算机 = 学生，周围的环境 = 老师。

最终目标：根据在学习过程中获得的经验技能，对没学习过的问题也可以做出正确解答，使计算机获得这种泛化能力。

应用：手写文字识别、声音处理、图像处理、垃圾邮件分类与拦截、网页检索、基因诊断、股票预测等。

典型任务：预测数值型数据的回归、预测分类标签的分类、预测顺序的排列。

2.2 无监督学习

给系统一堆无标签数据，它必须自己检测模式和关系。 系统要用推断功能来描述未分类数据的模式。

定义：指在没有老师的情况下，学生自学的过程。 在机器学习中，计算机从互联网中自动收集信息，并获取有用信息。

最终目标：无监督学习不局限于解决有正确答案的问题，所以目标可以不必十分明确。

应用：人造卫星故障诊断、视频分析、社交网站解析、声音信号解析、数据可视化、监督学习的前处理工具等。

典型任务：聚类、异常检测。

2.3 强化学习

强化学习其实是一个连续决策的过程，这个过程有点像有监督学习，只是标注数据不是预先准备好的，而是通过一个过程来回调整，并给出“标注数据”。

定义：指在没有老师提示的情况下，自己对预测的结果进行评估的方法。通过这样的自我评估，学生为了获得老师的最高价将而不断的进行学习。 强化学习被认为使人类主要的学习模式之一。

最终目标：使计算机获得对没学习过的问题也可以做出正确解答的泛化能力。

应用：机器人的自动控制、计算机游戏中的人工智能、市场战略的最优化等。

典型任务：回归、分类、聚类、降维。

3. 机器学习任务

在机器学习中，要解决某一问题，通常把问题转为成分类、回归、聚类、强化学习这四类问题进行解决。

3.1 分类问题

根据数据样本上抽取出的特征，判定其属于有限个类别中的哪一个。在实际中做分类的时候，大多会产出一个概率值，对概率值做排序得到该样本属于哪个类别的概率最高。

应用：垃圾邮件识别，结果类别为垃圾邮件和正常邮件；文本情感褒贬分析，结果类别褒、贬。

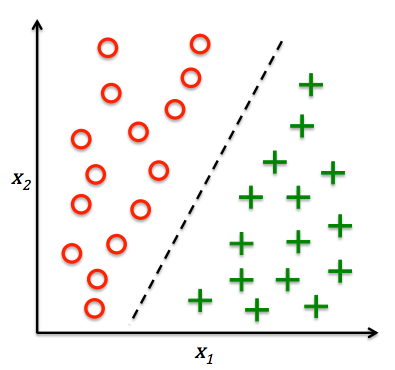
3.2 回归问题

根据样本上抽取的特征，预测连续值结果。属于有监督学习。

应用：预测电影的票房值，预测某城市的房价等。

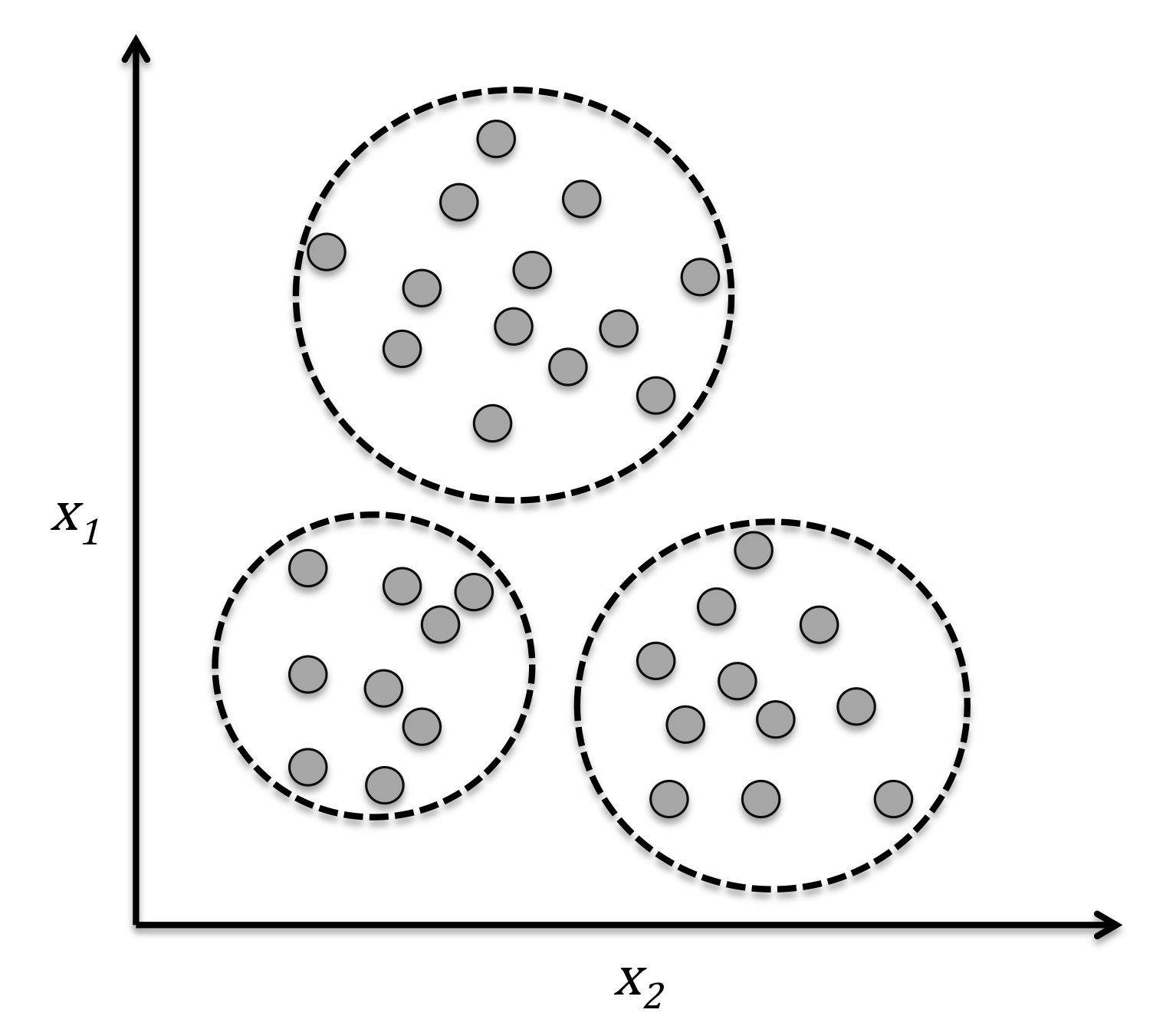
3.3 聚类问题

根据数据样本抽取的特征，挖掘出数据的关联模式。

应用：相似用户挖掘、新闻聚类等。

3.4 强化学习

研究如何基于环境而行动，以获得最大和的预期收益。

应用：在游戏开发中可能会用到，获取最高的分；机器人任务的完成

4. 基本术语

监督学习的算法是有标签的，或者说在数据中会有一部分是带参考答案的数据，然后在这些样本之上进行学习。如图所示，引用西瓜书的课件。

每一条记录为：一个实例（instance）或样本（simple）

数据集：所有记录的集合 ；

训练集：含有参考答案的数据，训练集还可以分成训练集和验证集；

测试集：用于实际预测所用到的数据。

5. 机器学习流程

对于运用机器学习去完成一个问题的流程，通常分为四个步骤：数据预处理（Preprocessing）、模型学习（Learning）、模型评估（Evaluation）、新样板预测（Prediction）。如图所示：

前三个环节都线下的部分，最后新样板的预测时线上的部分。第四个部分是开发部分的内容。主要影响结果是前三个部分。

数据预处理：通常会把原始的数据抽取出来，做一些数据的清洗，做一些特征工程的操作，特征抽取、幅度缩放、特征选择、维度约减等。

模型学习：在这一部分通常会做模型选择、交叉验证、结果评估、超参数选择等；

模型评估：会根据不同的场景选择评估标准。常用的评估标准是均方误差和平均绝对误差，但是有时会根据不同的场景选择或自定义评估标准，这些问题在kaggle上经常见到。

6. 机器学习库sklearn

6.1 简介

在机器学习中最常用的库是sklearn，它是站在巨人的肩膀上搭建起来的库，通常把机器学习的一些算法都封装好好了，只需要调用接口就可以实现某一个算法。在学习sklearn中最好的方式是通过sklearn的官方文档进行学习。

在sklearn的使用过程中常用的三个页面：scikit-learn Tutorials 入门页面；User Guide 算法指南页面，说明这个算法如何使用，如何实现等；API Reference 算法API。

6.2 sklearn算法

6.2.1 Scikit-Learn机器学习算法

from IPython.display import Image
%matplotlib inline

# Added version check for recent scikit-learn 0.18 checks
from distutils.version import LooseVersion as Version
from sklearn import __version__ as sklearn_version

6.2.2 机器学习算法选择

6.2.3scikit-learn初探

scikit-learn中自带了一些数据集，比如说最著名的Iris数据集。
数据集中第3列和第4列数据表示花瓣的长度和宽度。而类别已经转成了数字，比如
0=Iris-Setosa, 1=Iris-Versicolor, 2=Iris-Virginica.

from sklearn import datasets
import numpy as np

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target

print('Class labels:', np.unique(y))

Class labels: [0 1 2]

通常我们会把数据集切分成训练集和测试集，这里70%的训练集，30%的测试集。

if Version(sklearn_version) < '0.18':
    from sklearn.cross_validation import train_test_split
else:
    from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=0)

X_train.shape

(105, 2)

X_test.shape

(45, 2)

X.shape

(150, 2)

y_train.shape

(105,)

y_test.shape

(45,)

对特征做标准化

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()
sc.fit(X_train)

StandardScaler(copy=True, with_mean=True, with_std=True)

sc.scale_

array([ 1.79595918,  0.77769705])

X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

6.2.4 用scikit-learn中的感知器做分类

• 我们先用plot_decision_region函数来做一个可视化，方便一会儿直观看分类结果。
• 在这里不算重点，会与后面的深度学习有关联

from sklearn.linear_model import Perceptron

#ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)
ppn = Perceptron()

ppn.fit(X_train_std, y_train)

Perceptron(alpha=0.0001, class_weight=None, eta0=1.0, fit_intercept=True,
      max_iter=None, n_iter=None, n_jobs=1, penalty=None, random_state=0,
      shuffle=True, tol=None, verbose=0, warm_start=False)

ppn.coef_

array([[-1.48746619, -1.1229737 ],
       [ 3.0624304 , -2.18594118],
       [ 2.9272062 ,  2.64027405]])

ppn.intercept_

array([-1.,  0., -2.])

y_pred = ppn.predict(X_test_std)

y_pred

array([2, 1, 0, 2, 0, 2, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 2, 1, 0,
       0, 2, 0, 0, 1, 0, 0, 2, 1, 0, 2, 2, 1, 0, 2, 1, 1, 2, 0, 2, 0, 0])

y_test

array([2, 1, 0, 2, 0, 2, 0, 1, 1, 1, 2, 1, 1, 1, 1, 0, 1, 1, 0, 0, 2, 1, 0,
       0, 2, 0, 0, 1, 1, 0, 2, 1, 0, 2, 2, 1, 0, 1, 1, 1, 2, 0, 2, 0, 0])

y_pred == y_test

array([ True,  True,  True,  True,  True,  True,  True,  True,  True,
        True, False,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True, False,  True,  True,  True,  True,  True,  True,  True,
        True, False,  True,  True,  True,  True,  True,  True,  True], dtype=bool)

print('Misclassified samples: %d' % (y_test != y_pred).sum())

Misclassified samples: 3

from sklearn.metrics import accuracy_score

print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))

Accuracy: 0.93

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import warnings


def versiontuple(v):
    return tuple(map(int, (v.split("."))))

# 可视化作用，绘制决边界
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):

    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
                    alpha=0.8, c=cmap(idx),
                    marker=markers[idx], label=cl)

    # highlight test samples
    if test_idx:
        # plot all samples
        if not versiontuple(np.__version__) >= versiontuple('1.9.0'):
            X_test, y_test = X[list(test_idx), :], y[list(test_idx)]
            warnings.warn('Please update to NumPy 1.9.0 or newer')
        else:
            X_test, y_test = X[test_idx, :], y[test_idx]

        plt.scatter(X_test[:, 0],
                    X_test[:, 1],
                    c='',
                    alpha=1.0,
                    linewidths=1,
                    marker='o',
                    s=55, label='test set')

用标准化的数据做一个感知器分类器

%matplotlib inline
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

plot_decision_regions(X=X_combined_std, y=y_combined,
                      classifier=ppn, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')

plt.tight_layout()
# plt.savefig('./figures/iris_perceptron_scikit.png', dpi=300)
plt.show()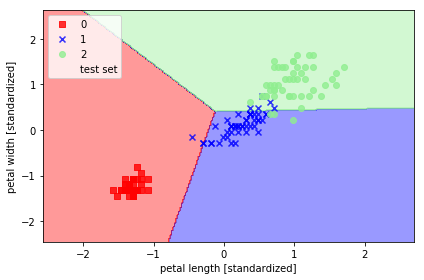

6.2.5 通过逻辑回归预测属于每个类别的概率

(1). LR的简单复习

# sigmoid函数，通过选择合适的阈值来做分类
import matplotlib.pyplot as plt
import numpy as np


def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)

plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')

# y axis ticks and gridline
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)

plt.tight_layout()
# plt.savefig('./figures/sigmoid.png', dpi=300)
plt.show()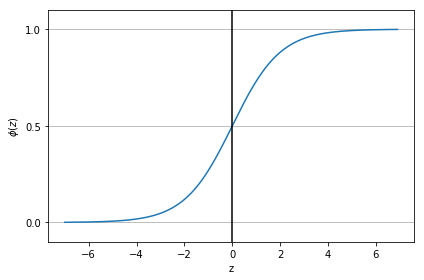

Image(filename='./images/03_03.png', width=500)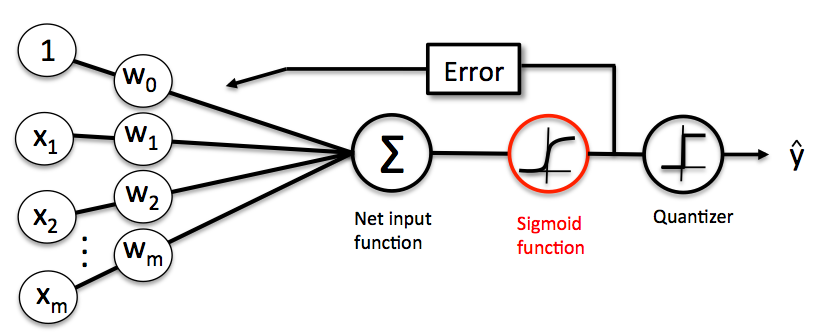 

通过最小化损失函数求解权重

# 损失函数
def cost_1(z):
    return - np.log(sigmoid(z))


def cost_0(z):
    return - np.log(1 - sigmoid(z))

z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)

c1 = [cost_1(x) for x in z]
plt.plot(phi_z, c1, label='J(w) if y=1')

c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0')

plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc='best')
plt.tight_layout()
# plt.savefig('./figures/log_cost.png', dpi=300)
plt.show()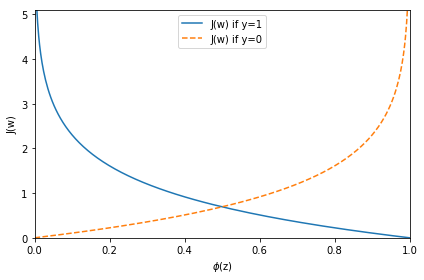

(2). 使用scikit-learn训练LR

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(C=1000.0, random_state=0)
lr.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined,
                      classifier=lr, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/logistic_regression.png', dpi=300)
plt.show()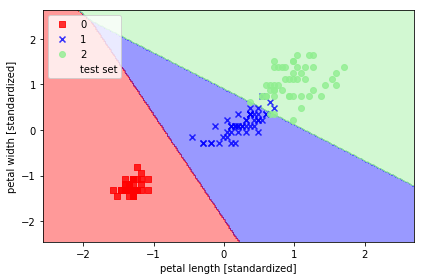

if Version(sklearn_version) < '0.17':
    lr.predict_proba(X_test_std[0, :])
else:
    lr.predict_proba(X_test_std[0, :].reshape(1, -1))

X_test_std[0,:]

array([ 0.70793846,  1.50872803])

X_test_std[0,:].reshape(1, -1)

array([[ 0.70793846,  1.50872803]])

lr.predict_proba(X_test_std[0,:].reshape(1, -1))

array([[  2.05743774e-11,   6.31620264e-02,   9.36837974e-01]])

6.2.6 过拟合/overfitting 与 正则化/regularization

weights, params = [], []
for c in np.arange(0, 5):
    lr = LogisticRegression(C=10**c, random_state=0)
    lr.fit(X_train_std, y_train)
    weights.append(lr.coef_[1])
    params.append(10**c)

weights = np.array(weights)
plt.plot(params, weights[:, 0],
         label='petal length')
plt.plot(params, weights[:, 1], linestyle='--',
         label='petal width')
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.legend(loc='upper left')
plt.xscale('log')
# plt.savefig('./figures/regression_path.png', dpi=300)
plt.show()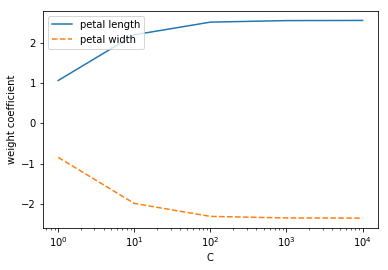

6.2.7 最大间隔分类与支持向量机

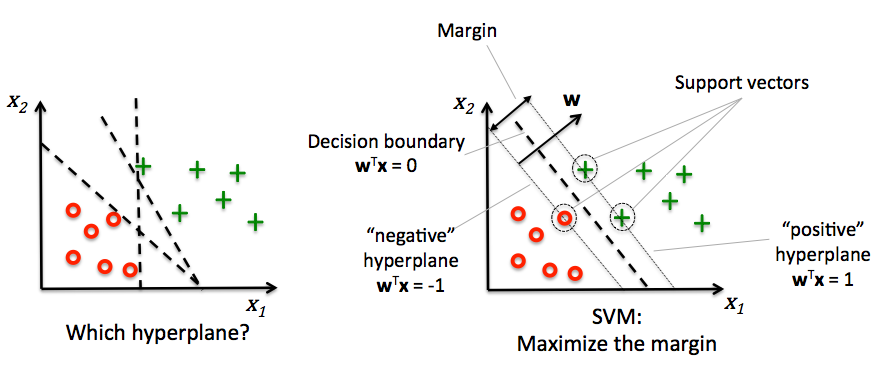
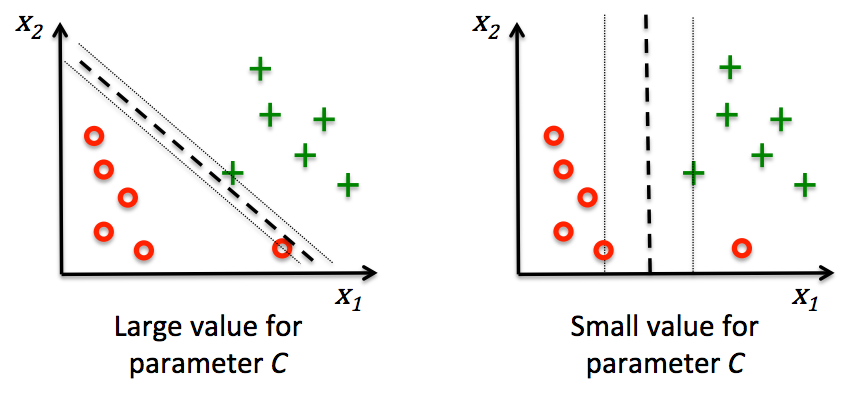
(1). 通过松弛变量解决非线性切分情况

from sklearn.svm import SVC

svm = SVC(kernel='linear', C=1.0, random_state=0)
svm.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined,
                      classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/support_vector_machine_linear.png', dpi=300)
plt.show()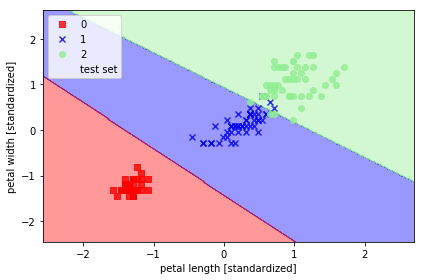

(2). 神奇的SVM核函数完成非线性切分

import matplotlib.pyplot as plt
import numpy as np

np.random.seed(0)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0,
                       X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)

plt.scatter(X_xor[y_xor == 1, 0],
            X_xor[y_xor == 1, 1],
            c='b', marker='x',
            label='1')
plt.scatter(X_xor[y_xor == -1, 0],
            X_xor[y_xor == -1, 1],
            c='r',
            marker='s',
            label='-1')

plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='best')
plt.tight_layout()
# plt.savefig('./figures/xor.png', dpi=300)
plt.show()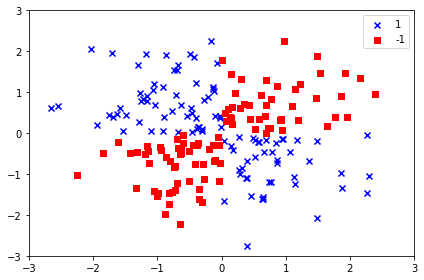

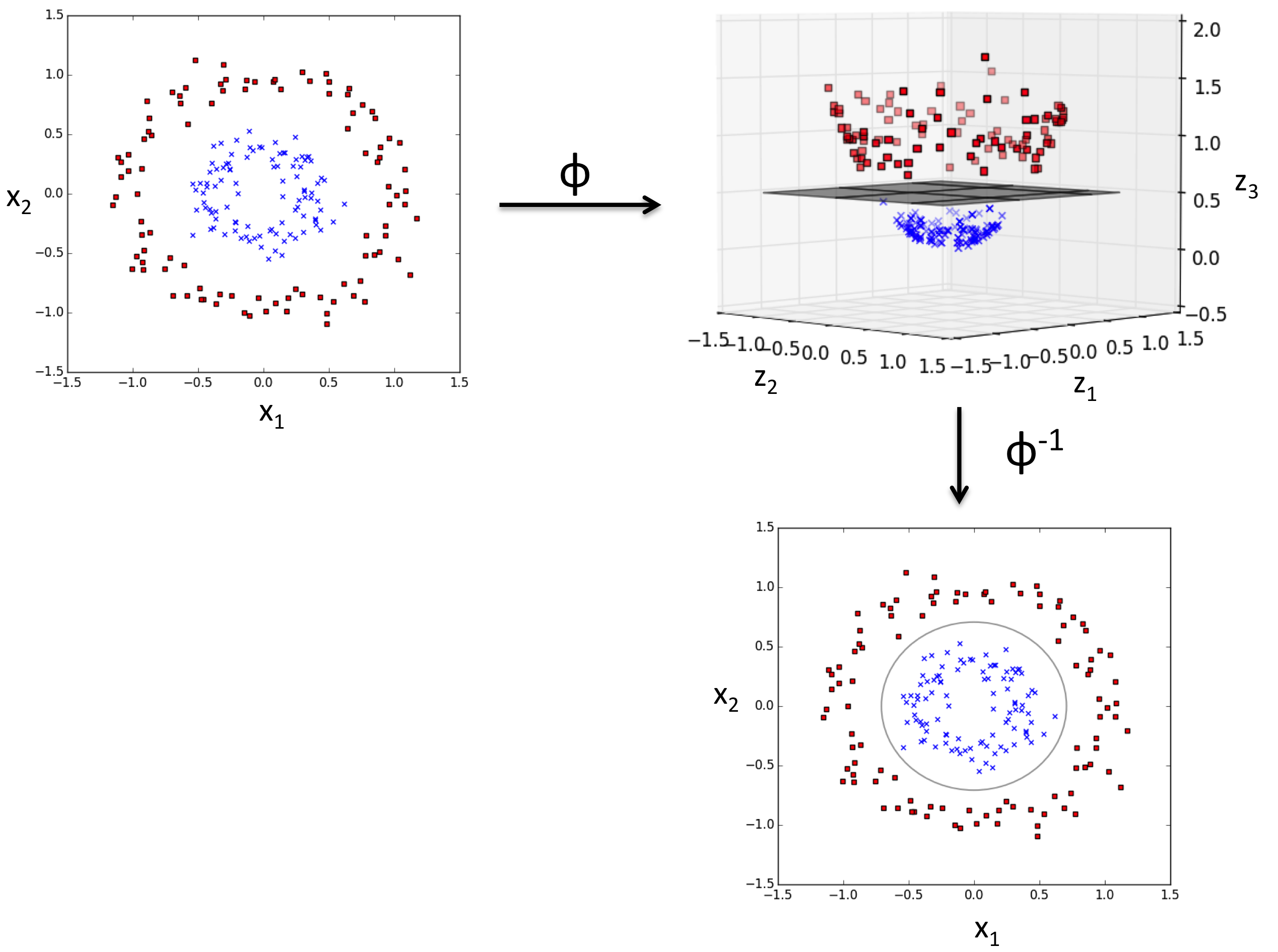
使用kernel trick在高维空间内找到一个可切分的超平面

svm = SVC(kernel='rbf', random_state=0, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor,
                      classifier=svm)

plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/support_vector_machine_rbf_xor.png', dpi=300)
plt.show()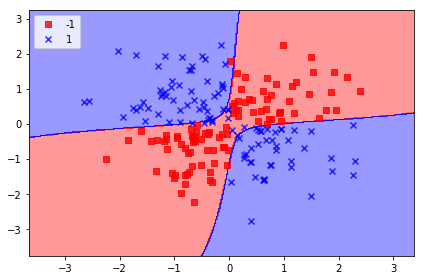

from sklearn.svm import SVC

svm = SVC(kernel='rbf', random_state=0, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined,
                      classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/support_vector_machine_rbf_iris_1.png', dpi=300)
plt.show()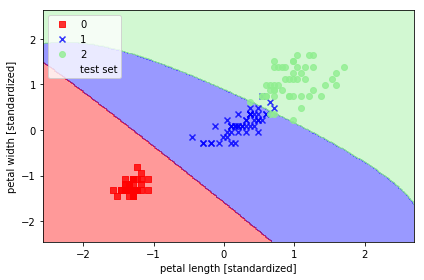

svm = SVC(kernel='rbf', random_state=0, gamma=100.0, C=1.0)
svm.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined, 
                      classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/support_vector_machine_rbf_iris_2.png', dpi=300)
plt.show()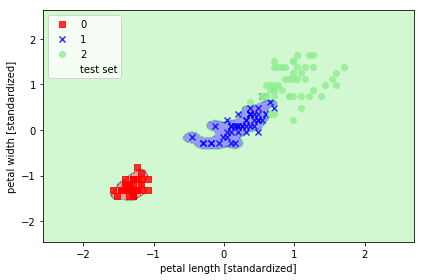

6.2.8 决策树学习

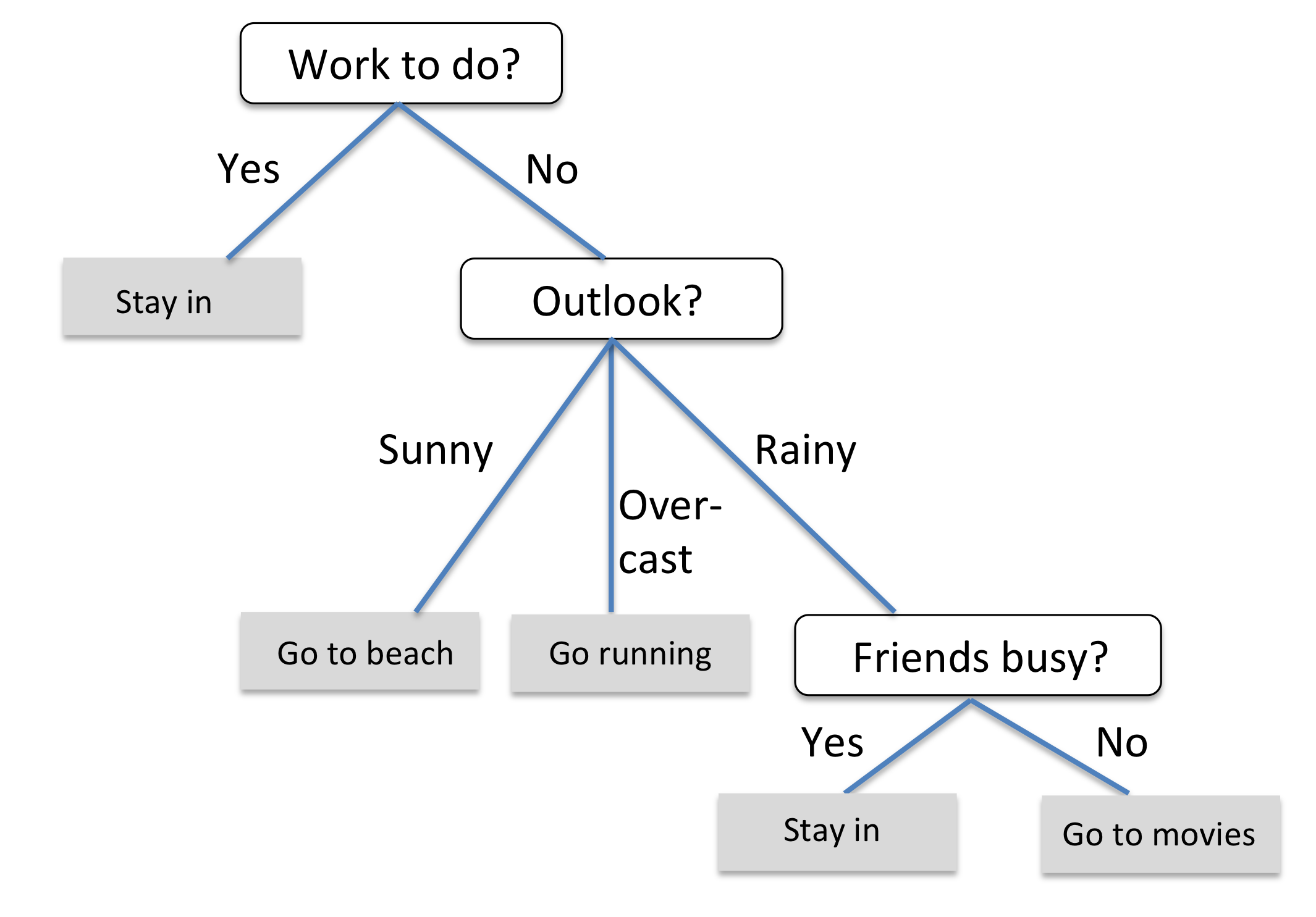
(1). 最大化信息增益，找到最好的切分点

import matplotlib.pyplot as plt
import numpy as np


def gini(p):
    return p * (1 - p) + (1 - p) * (1 - (1 - p))


def entropy(p):
    return - p * np.log2(p) - (1 - p) * np.log2((1 - p))


def error(p):
    return 1 - np.max([p, 1 - p])

x = np.arange(0.0, 1.0, 0.01)

ent = [entropy(p) if p != 0 else None for p in x]
sc_ent = [e * 0.5 if e else None for e in ent]
err = [error(i) for i in x]

fig = plt.figure()
ax = plt.subplot(111)
for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err], 
                          ['Entropy', 'Entropy (scaled)', 
                           'Gini Impurity', 'Misclassification Error'],
                          ['-', '-', '--', '-.'],
                          ['black', 'lightgray', 'red', 'green', 'cyan']):
    line = ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c)

ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15),
          ncol=3, fancybox=True, shadow=False)

ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
plt.ylim([0, 1.1])
plt.xlabel('p(i=1)')
plt.ylabel('Impurity Index')
plt.tight_layout()
#plt.savefig('./figures/impurity.png', dpi=300, bbox_inches='tight')
plt.show()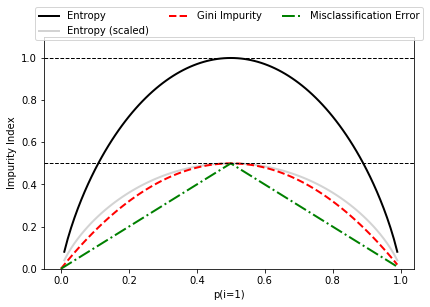

(2). 建一颗决策树

from sklearn.tree import DecisionTreeClassifier

tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=0)
tree.fit(X_train, y_train)

X_combined = np.vstack((X_train, X_test))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X_combined, y_combined, 
                      classifier=tree, test_idx=range(105, 150))

plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/decision_tree_decision.png', dpi=300)
plt.show()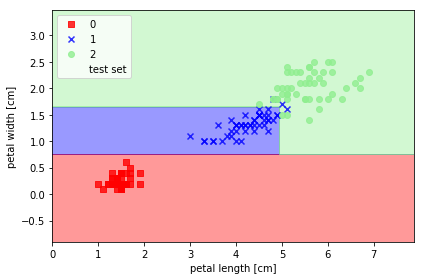

from sklearn.tree import export_graphviz

dot_data = export_graphviz(tree, 
                out_file='tree.dot', 
                feature_names=['petal length', 'petal width'])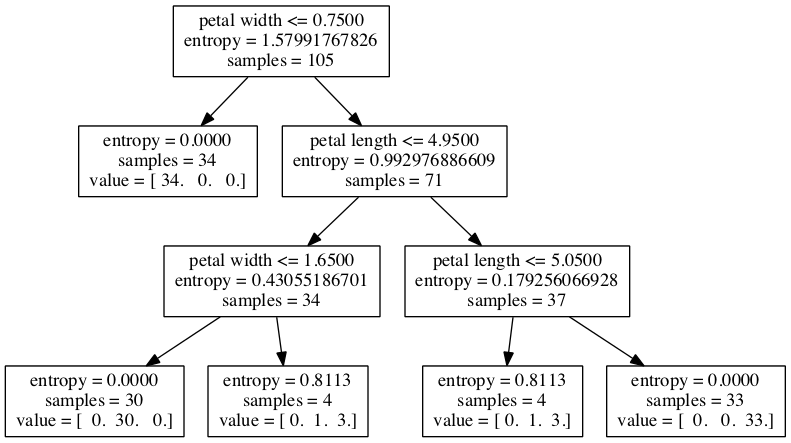

Note

If you have scikit-learn 0.18 and pydotplus installed (e.g., you can install it via pip install pydotplus), you can also show the decision tree directly without creating a separate dot file as shown below. Also note that sklearn 0.18 offers a few additional options to make the decision tree visually more appealing.

import pydotplus

from IPython.display import Image
from IPython.display import display

if Version(sklearn_version) >= '0.18':

    try:

        import pydotplus

        dot_data = export_graphviz(
        tree, 
        out_file=None,
        # the parameters below are new in sklearn 0.18
        feature_names=['petal length', 'petal width'],  
        class_names=['setosa', 'versicolor', 'virginica'],  
        filled=True,
        rounded=True)

        graph = pydotplus.graph_from_dot_data(dot_data)  
        display(Image(graph.create_png()))

    except ImportError:
        print('pydotplus is not installed.')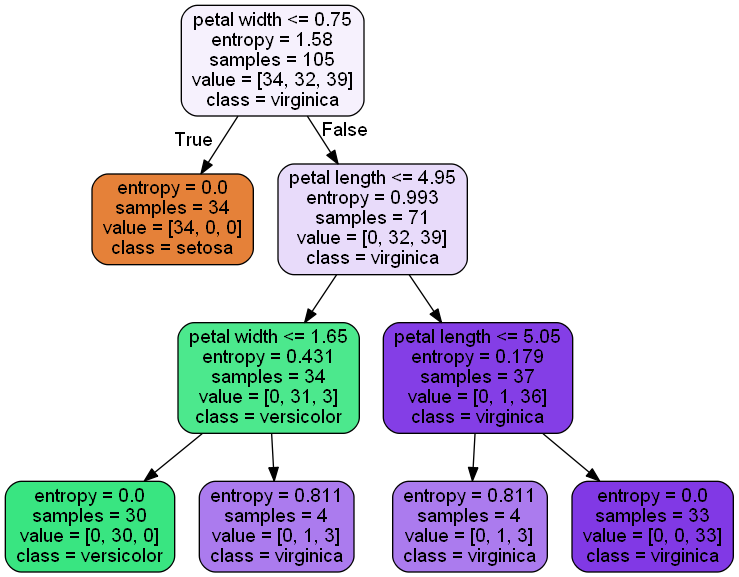

(3). 使用随机森林对树做叠加，变成增强分类器

from sklearn.ensemble import RandomForestClassifier

forest = RandomForestClassifier(criterion='entropy',
                                n_estimators=10, 
                                random_state=1,
                                n_jobs=2)
forest.fit(X_train, y_train)

plot_decision_regions(X_combined, y_combined, 
                      classifier=forest, test_idx=range(105, 150))

plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/random_forest.png', dpi=300)
plt.show()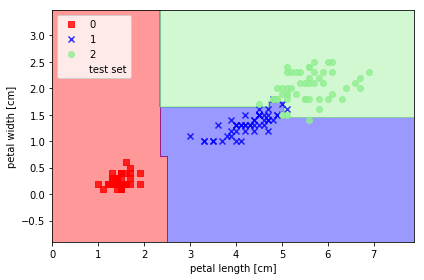

6.2.9 K最近邻，朴素的分类器

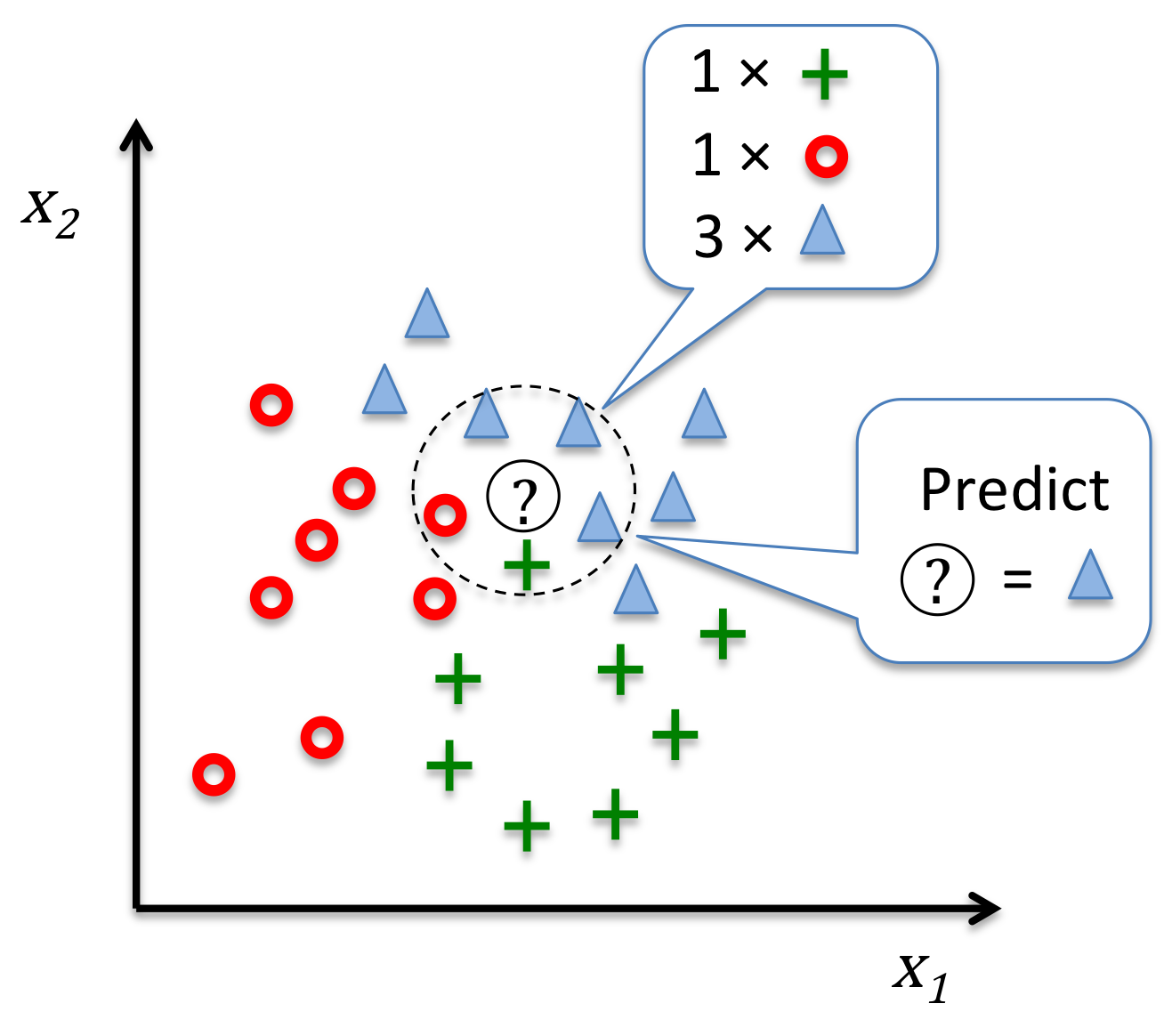
from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski')
knn.fit(X_train_std, y_train)

plot_decision_regions(X_combined_std, y_combined, 
                      classifier=knn, test_idx=range(105, 150))

plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/k_nearest_neighbors.png', dpi=300)
plt.show()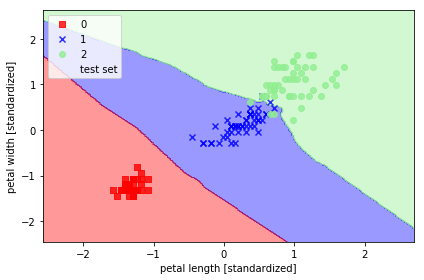

bug解决

1.graphviz找不到问题

7.数据处理

这部分主要是解决机器学习中数据的处理问题，主要是应用代码来实现相应的操作，代码部分放在GitHub中可以找到。

8.回归问题与建模分析

主要是对回归问题的建模与分析结合例子来讲解回归问题，主要是运用代码实现问题的解决过程，实现的代码在GitHub中可以找到。

参考文献：

1.机器学习的种类及其典型的任务

2.七月在线课件