对EEG/MEG微状态分析的动态理解

摘要：具有时间稳定且空间一致的活动模式的脑电图被称为微状态，与各种认知和临床现象有关。多个研究表明微状态时间序列可能揭示大脑在静息状态下的神经活动，然而，关于微状态分析的解释仍然没有一致意见。多种聚类算法已用于微状态计算。本研究主要解决现有的两个问题。首先，通过将几种最先进的微状态算法应用于大量 EEG 记录的数据集，旨在表征和描述各种微状态算法。演示并讨论为何三种“经典”算法（T)AAHC 和修改的 K-Means）产生几乎相同的结果，而 HMM 算法生成最不相似的结果。其次，检验微状态属性在很大程度上可能由基础 EEG 信号的线性特征，特别是 EEG 数据的交叉协方差和自相关结构决定的假设。通过生成 EEG 信号的傅里叶变换替代物以比较微状态属性。发现微状态属性在很大程度上取决于基础 EEG 数据的线性协方差和自相关结构。最后，将 EEG 数据视为矢量自回归过程，估计了其参数，并从拟合的 VAR 生成了替代的稳态和线性数据。观察到这样的线性模型生成的微状态与从真实 EEG 数据估计的微状态非常相似，支持了线性 EEG 模型可以帮助解释静态和动态人脑微状态属性的结论。

前言

Lehmann等人（1987年）首次展示了多通道静息状态EEG信号的alpha频带（8-12 Hz）可被划分为有限数量的准稳态，被认为是“思维的基本单元”。微状态分析用于描述行为状态、人格类型和神经精神障碍的变异性。对于微状态分析的有效性存在争议，尤其是关于大脑是否真的在相对较低和固定数量的离散状态之间转换的基本假设。有研究探讨了大脑动态的低维流形，认为亚稳态动力学支配了大脑活动。一些研究比较了各种聚类算法，发现微状态聚类方案和线性方法之间存在相似性。研究者提出了一个假设，即动态微状态属性可能可以从潜在EEG信号的线性特征中获取。本研究通过使用傅里叶变换替代EEG信号，将EEG数据视为稳态矢量自回归过程，发现微状态属性与潜在EEG数据的线性特征相关，支持线性EEG模型解释微状态属性。该研究通过应用多种微状态算法评估它们在检测和表征微状态方面的性能，并比较各种算法，为有兴趣利用EEG微状态获得大脑功能洞见的研究人员提供资源。同时，研究评估了微状态属性是否可以直接从潜在EEG数据的线性特征中获取，为EEG微状态研究领域提供了重要理论贡献。

材料和方法

微状态分析的过程

在微状态分析中，多通道脑电图（EEG）信号以（通道，时间）的2D矩阵形式表示电位瞬时地形的序列。在信号聚类之前，提取全局场功率（GFP）峰值，以考虑信噪比最高的时间点。微状态分析包括两个步骤：首先，识别代表性的微状态地形图；其次，将原始多通道脑电图记录投影到这些微状态地形图上，形成脑电信号的离散微状态地形图序列。每个算法产生一组代表脑电数据集的微状态地形图。找到代表性微状态地形图后，通过以下过程将原始多通道脑电图记录转换为微状态地形图的时间序列：为每个GFP峰分配一个规范地图，然后将微状态标识根据时间上最接近的GFP峰传播到其他时间点。

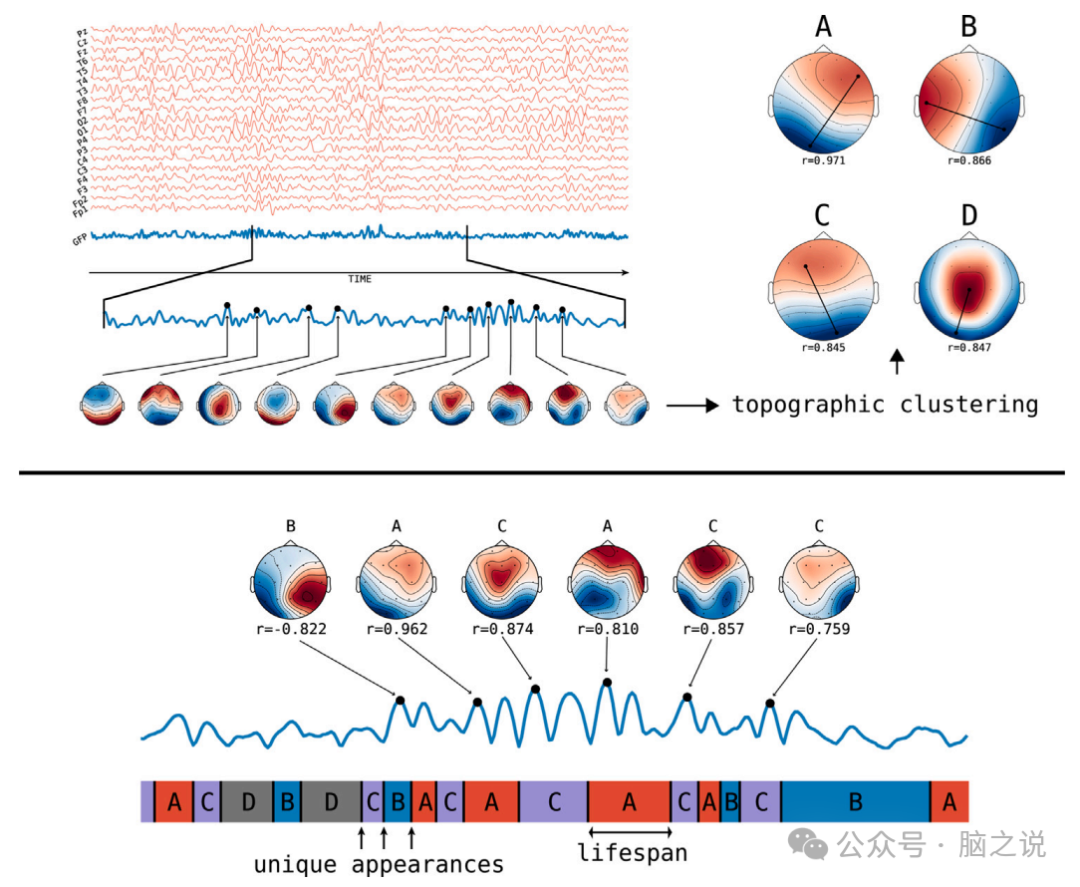
图1. 微观状态分析方法的示意图和从微观状态时间序列中提取感兴趣的特征，改编自Khanna等人（2014）

微状态分析的微状态序列计算在所有聚类方法中都是相同的，采用“胜者通吃”或竞争反向拟合方法。常用的评估微状态序列与基础脑电数据集的拟合程度的指标是全局解释方差（GEV），它衡量了微状态地形图解释数据方差的百分比。

在我们的研究中，所有聚类算法都有可能产生不同数量的微状态地形图，因为聚类数是方法的参数。为了确保兼容性和减少不必要的复杂性，我们选择在所有算法中使用固定数量的四个微状态地形图，与该领域的早期重要工作和最新研究保持一致。生成的微状态地形图按照Koenig等人（2002）提供的模板地形图进行排序，以便于复制和算法之间的比较。

聚类算法

(Topographic) atomize and agglomerate hierarchical clustering（AAHC和TAAHC）是最常用的微状态聚类算法之一。这两种算法都是确定性的层次聚类算法。它们都采用自下而上的方法，即将每个EEG地形图作为单独的聚类进行初始化，然后迭代地减少聚类数。在每次迭代中，最差的聚类被分解，所有以前的成员都被重新分配到一个聚类中。然后，通过最大相似性来更新聚类中心。当达到预先选择的聚类数时，算法结束。这两种算法的结果如图2和图3所示。

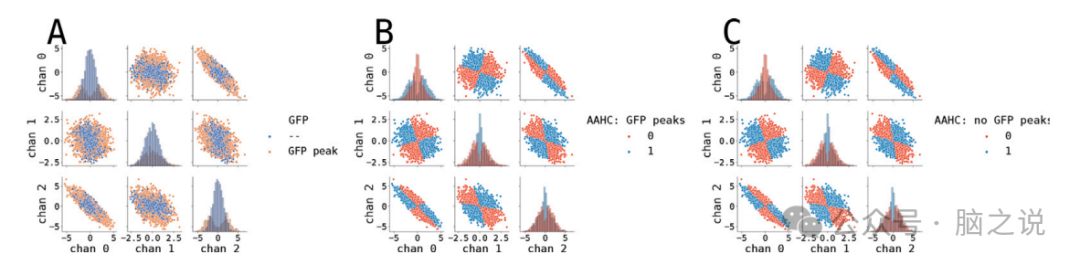
图2.基于合成数据的AAHC聚类算法结果。一个合成的三维数据集，作为长度为10 s的多元正态分布，采样率为250Hz。（A）数据分布，其中GFP峰用橙色表示。请注意，GFP的峰值是如何位于数据云的边缘上的。（B)AAHC算法在仅使用GFP峰的合成数据上的应用。（C)AAHC算法在使用所有可用数据点的合成数据上的应用。

 图3. 基于合成数据的TAAHC聚类算法结果。

这两种自下而上的算法在使用GFP峰值或整个合成时间序列进行预处理时都显示出非常相似的分割结果。GFP预处理不会改变分割结果的原因很简单：由于这两种算法都是自下而上的，它们仅将最相似的聚类合并在一起（AAHC和TAAHC仅在聚合标准上有所不同）。在AAHC算法中，那些不是GFP峰值（因此具有低方差（GEV））的地形图被合并到具有更高GEV的聚类中（因此是GFP峰值的地形图）。然后，由于聚类中心在（T）AAHC中由第一个特征向量定义，这些低GEV地图对最终聚类中心的影响只有微不足道的影响。对于TAAHC也是类似的。为了量化相似性效应，我们还使用Spearman相关性计算了仅使用GFP峰值运行和整个数据运行的分割之间的相似性度量，这些度量伴随着分析p值和准确性acc，使用基于排列的acc值进行统计。

Modified K-means是历史上最早用于微状态分析的算法之一。它是一种迭代随机聚类算法，灵感来自经典的K-means聚类。该算法使用随机选择的GFP峰值地形图作为聚类中心进行初始化，并通过两步迭代的方式估计微状态序列，然后根据序列更新聚类中心。迭代继续进行，直到聚类中心不再改变为止。由于算法初始化的随机性，不同的运行可能会产生不同的微状态地形图和分配结果。仅使用GFP曲线峰值进行预处理不会显著改变分割结果，因为该算法按照一种自然的方式进行迭代，使最终的聚类中心偏向于远离中心的地形图，这些地形图也是GFP峰值选择的地形图。使用Spearman相关性和准确性度量量化了仅使用GFP峰值和整个数据运行的分割之间的相似性。

主成分分析（PCA）是微状态分析中常用的降维方法之一。空间PCA先前已用于聚类EEG地形图的研究中。PCA通过对数据协方差矩阵进行特征分解来计算，其中主成分对应于矩阵的特征向量。PCA自然地根据各自的特征值对组件进行排序，并且组件是相互正交的。PCA是确定性的，并且有助于提高可重复性。

独立成分分析（ICA）是神经科学应用中另一种广泛使用的分解技术。ICA寻求组件之间的统计独立性，执行信号分离。本研究中使用的特定实现是Fast-ICA。信号分离通常写作

，其中

包含GFP峰值处的EEG数据的转置矩阵，W表示分离矩阵，S是源矩阵。

隐藏马尔可夫模型（HMM）是一种生成模型，描述了由隐藏状态的快速切换产生的观测结果，采用了高斯发射模型。HMM已成功用于分析静息态MEG数据，并将其与fMRI中研究的经典静息态网络进行比较。

微状态测量

在本研究中，使用了多个摘要统计量来描述从各种聚类算法中推断出的序列的时间特征。为了计算统计数据，使用了从算法直接获得的潜在状态的序列（例如，对于ICA和PCA，每个时间步的最大激活，对于HMM，使用了维特比解码等），尽管这些序列已被重新标记，以使微状态地形图与Koenig等人200年的模板相匹配，确保了受试者和算法之间的可比性，例如，状态A对应于所有受试者和所有聚类算法的基于文献的模板微状态（Koenig等人，2002）。

计算指标

1）平均寿命；微状态的寿命被计算为所有连续原始数据点被分配相同微状态类的时间（Lehmann等人，2005）（参见图1B），即

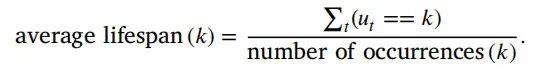
。2）覆盖率；微状态的覆盖率通过将在特定微状态中花费的总时间与总记录时间的比率来计算（Lehmann等人，2005）

。3）出现次数；微状态频率是通过计算在一秒的记录中微状态的独特出现次数来确定的（Lehmann等人）

。

实验数据和合成数据

实验数据来自Max Planck Institut Leipzig Mind-Brain-Body数据集（LEMON），包括228名健康参与者的EEG数据。EEG数据在静息状态下使用两种范式进行采集：睁眼和闭眼。数据集包括年轻和老年参与者，提供了采样频率为250 Hz，长度约为8分钟的预处理EEG数据。

为了评估微状态分析流程在类似真实EEG数据的随机数据上的表现，该研究使用了多元傅里叶变换伪数据，也称为随机相位。这些伪数据保留了谱内容和自相关函数，同时破坏了任何时间尺度之间的关系。伪数据过程产生了与原始EEG数据相同长度和采样率的时间序列数据，并使用固定种子的随机数生成器以便在参与者之间进行比较。

此外，该研究采用向量自回归（VAR）过程来测试微状态属性是否可以从线性协方差和自协方差结构中估计。对于每个参与者，估计VAR过程的阶数，并使用随机初始化为每个参与者模拟VAR过程1200或3600秒。然后，在完整的VAR数据上以及不同长度的段上运行微状态分析，并对这些段的属性进行平均,

计算方法和实施方案

所有分析，包括聚类算法、所有测量和统计测试均在Python 3.7版本中实施。对于实验数据的加载和处理，研究依赖于mne库（Gramfort等，2013年）。对于独立成分分析（ICA）和主成分分析（PCA）聚类算法，使用了scikit-learn库的实现。对于隐马尔可夫模型，使用了hmmlearn库，对于其他聚类算法，研究编写了自定义实现。整个代码库可以在N.J.的GitHub上找到。

结果

1.对6种聚类算法在简单的合成数据上进行了评估

为了方便可视化，研究选择生成3D多元正态数据，采用平均参考，模拟了一个3通道的EEG脑电图，采样率为250 Hz。研究在两种方式下运行聚类算法：仅使用GFP峰值或整个时间序列，以评估这种转换的影响。研究发现，选择GFP峰值相当于在时间上进行非等距子采样，并选择在相空间中远离平均值的值，即在多通道维度中的多元数据云的边缘。

研究评估了两种基于层次聚类的经典微状态算法：原子化和聚合层次聚类及其拓扑版本。这两种算法都是自下而上的，即它们都是以每个EEG拓扑图作为单独的聚类开始，然后迭代地合并这些聚类以形成最终的4个聚类。研究发现，这两种自下而上的算法在使用GFP峰值或整个合成时间序列进行预处理时，都显示出非常相似的分割结果。这是因为这两种算法都是纯粹地将最相似的聚类合并在一起（AAHC和TAAHC仅在聚合标准上有所不同）。在AAHC算法的情况下，那些不是GFP峰值的拓扑图（因此具有低方差（GEV））被合并到具有更高GEV的聚类中（因此是GFP峰值的拓扑图）。然后，由于聚类中心在（T）AAHC中由第一个特征向量定义，这些低GEV的地图对最终聚类中心的影响只有微不足道的作用。类似的论点适用于TAAHC。为了量化相似性效应，研究还使用Spearman相关性计算了仅使用GFP峰值运行和整个数据运行的分割之间的相似性度量，使用解析p值和使用基于排列p的值进行统计评估的准确性。

研究还评估了修改后的K均值算法，发现在使用GFP峰值或整个合成时间序列进行预处理时，该算法的分割结果也非常相似。研究还手动交换了聚类分配，以确保算法的极性切换时的相似性。对于AAHC算法，相似性达到了r(2500) = 0.995，p<0.001和r=0.998，p<0.001（20000次排列），而对于TAAHC算法，相似性达到了r(2500) = 0.993，p<0.001和acc=0.996，p<0.001（20000次排列）。修改后的K均值算法是微状态分析中最初经典使用的聚类算法。研究将修改后的K均值算法应用于合成数据集，以找到2个微状态图。研究发现，当仅使用GFP曲线的峰值进行预处理时，分割结果并未发生显著变化。这是由于算法的迭代性质，首先通过将输入向量投影到聚类中心并找到最大负荷的方向来计算输入拓扑的分配。然后，它重新计算聚类中心，作为该聚类拓扑的加权平均值，其权重为特定地图的欧氏范数。距离加权自然地使最终的聚类中心偏向于更远的拓扑图，这也是GFP峰值选择的拓扑图。两种相似性度量显示GFP和非GFP分割之间非常高的相似性（r(2500) = .945, p< 0.001，和acc = 0.972，p< 0.001（20000次排列））。

图4. 合成数据的K-Means聚类算法结果。

应用隐藏马尔可夫模型的结果如图5所示。HMM算法的GFP和非GFP情况的分割结果存在显著差异。这主要是由于HMM中的观测模型是高斯模型。当我们使用GFP预处理时，我们选择离中心更远的点（见图5A）。鉴于数据在所有维度上并不具有相同的协方差，这也意味着数据有效地将云分成了两半（至少在一个维度上），因此HMM算法将以使两个聚类尽可能接近多元高斯分布的方式将云分成两个聚类（参见图5B中对角线上的直方图）。当我们不使用GFP峰值预处理时，HMM算法正确估计整个数据云是一个多元高斯分布。因此，它将所有点分配给同一聚类（图5C）。自然地，这两种方法之间的相似性非常低（r(2500) = 0.021, p = 0.298, acc= 0.520, p= 0.480 （20000次排列））。

图5. 在合成数据上的隐马尔可夫模型聚类算法的结果。

用PCA和ICA对脑电图拓扑图进行聚类。结果表明，无论采用哪种预处理方法，PCA和ICA聚类都产生非常相似的分割结果，具有很高的相似性度量。PCA虽然不严格属于微状态算法，但它是确定性的，并且对于可重复性非常有价值。它基于最高方差选择第一个主成分，导致无论使用何种预处理方法，都能产生一致的分割结果。同样，ICA聚类也针对两种预处理情况产生了非常相似的分割结果，表明预处理方法的选择并不显著影响聚类结果。

图6. 主成分分析聚类算法结果。

 图7. 独立成分分析聚类算法结果。

因此，除了隐藏马尔可夫模型外，所有测试的算法在两种预处理情况下都产生了类似的分割结果。选择GFP峰值的唯一理由可能是计算速度，特别是对于自下而上的凝聚（T）AAHC算法。综合三种经典微状态算法（AAHC、TAAHC和改进的K均值算法）的结果表明，无论是否选择GFP峰值，这些算法的分割准确度均达到0.9（见图8左侧）。相比之下，PCA和ICA之间的分割差异最大，准确度约为0.2。此外，除了使用GFP峰值预处理的改进的K均值算法外，所有六种实施的算法的拓扑图（即聚类中心）非常相似（见图8右侧）。在两种预处理选项下，三种经典微状态算法产生了类似的静态微状态统计数据（覆盖率、寿命和出现次数）。在覆盖率方面，最不相似的算法是PCA和HMM。这两种算法还产生了不同的动态统计数据，主要是熵。

图8. 利用6种算法进行潜在分解。（左）左上角显示了6种不同预处理选项（GFP或no GFP）的微观状态算法计算的分割相似性。用于量化相似性的测量方法是准确性。（中）使用皮尔逊相关性，在左下角显示了每个算法产生的地形（聚类中心）的相似性。（右）微观状态属性；最上面一行显示了GFP峰值预处理的覆盖范围、寿命和出现情况（底部一行显示了没有GFP峰值的覆盖率、寿命和预处理的出现情况。

2.对模拟受试者数据进行分析

我们生成了更加真实的合成数据，增加了更多的通道，并模拟了受试者间的差异，通过使用不同的随机种子生成了200个数据样本，因此每个“受试者”都具有不同的正定协方差矩阵。为了进一步扩展我们的分析，并弥合之前的合成数据集与接下来更为真实的替代数据集以及最终的实验数据集之间的差距，我们生成了包含20个通道并寻找4个微状态的合成数据集。在这种情况下，我们仍然只使用了GFP峰值选择预处理，这在微状态分析中是典型的。在这种情况下，我们仍然使用时间独立且相同分布的随机变量，因此微状态的寿命和出现次数要短得多。所有六种测试算法在建模受试者间方差方面都相对稳定（即分割准确度和拓扑图相关性的标准偏差较低，不同测量指标的方差也较低），除了HMM。特别是HMM在覆盖率和出现次数方面显示出相对较高的受试者间方差。此外，我们观察到在我们的合成数据中，6种算法中有4种产生了对称的覆盖率（即所有4个状态的覆盖率约为0.25），除了前面提到的HMM和PCA。我们还注意到，由三种经典微状态算法（AAHC、TAAHC和改进的K均值算法）产生的分解在GFP峰值和整个合成脑电图时间序列中解释了最高比例的方差，而PCA和ICA解释的方差比例略低。所有六种算法提供的时间序列分割具有相似的混合时间，其中有4种算法具有最高的熵（熵的上限是通过计算具有4个离散状态的均匀分布的熵得出的），而PCA略低，HMM明显较低（这与覆盖率有关）。

从合成数据集的结果来看，我们预计三种经典的微状态算法将提供非常相似的拓扑图、时间序列分割以及静态和动态微状态属性。我们还预计HMM算法在静态微状态属性、时间序列分割的熵以及所有测量中的受试者间方差方面表现与其他测试算法不同。有

3.对实验数据集进行分析

从202名受试者获取的静息状态眼睛睁开和闭合的脑电信号。经典的微状态算法（AAHC、TAAHC、修改的K-Means）显示出非常相似的几何形状，并且当所有4个状态与模板至少在0.9水平上相关时，与规范微状态图非常相似。这适用于两种脑电图范式（图10，前三列），尽管眼睛睁开的范式平均相关性更高。其他算法，即PCA、ICA和HMM显示出一些细微差异，尽管主要特征得到保留。总的来说，三种经典的微状态算法产生非常相似的拓扑图，并与规范模板微状态图高度相关。PCA和ICA的拓扑图在某种程度上相似，除了一些多模态图之外，总体上与规范模板的相关性较低。

图9. 使用6种算法进行潜在分解的200个模拟对象的合成数据集上的微观状态特性。（A）使用6种不同的微观状态算法计算受试者之间的平均±标准差。用于量化相似性的测量方法是准确性。（B）静态微观状态属性（覆盖范围、寿命和发生情况；每个潜在图（A-D）和每个算法）。（C）解释了每个算法的GFP峰值和整个时间序列中的方差。（D）每个算法使用皮尔逊相关性作为受试者之间的平均±标准差所产生的地形（聚类中心）的相似性。

图10. 在闭眼静息状态脑电图范式下的LEMON数据集的组水平微状态图。按行显示每个算法产生的四种微观状态，按列显示不同的算法。

4.微状态特性

6种算法得出的静态和动态微状态特性。图11分别展示了闭眼和睁眼静息状态脑电图的概览图。与合成数据相比，我们预计个体之间的异质性更大。这在分割相似性中立即可见（图11A）：三种经典微状态算法提供了最相似的分割，平均准确度（作为相似性度量）在0.5到0.6之间。其他算法彼此之间的准确度较低，并且与经典微状态图也较低。经典微状态算法（AAHC、TAAHC、修改的K-Means）产生非常相似的静态和动态微状态特性，包括覆盖率、寿命、发生率、混合时间、熵和熵率。PCA和ICA算法也产生类似的微状态特性，但与经典算法相比存在一些差异。HMM算法在静态微状态特性方面表现出更高的主观方差，较低的熵和熵率数值，以及时间序列分割的最低整体准确度。总的来说，不同聚类算法得出的微状态特性可能存在差异，突显了在进行脑电微状态分析时考虑微状态图的特征的重要性。

图11. 在闭眼静息状态下，LEMON数据集的潜在分割概述。(A）使用6种不同的微观状态算法计算的受试者之间分割的平均±标准差。用于量化相似性的测量方法的准确性。（B）每个潜在图（A-D）和每个算法静态微观状态属性（覆盖范围、寿命和发生情况）。每个图包含一个子图，它可视化了跨受试者的在a-d地图上平均的相关矩阵。（C）解释了每个算法的GFP峰值和整个时间序列中的方差。显示的也是受试者之间的相关矩阵。（D）地形的相似性（聚类中心）

5.比较合成数据和真实静息状态脑电图的微状态分析结果

经典微状态算法在两种情况下的统计数据非常相似。然而，HMM算法在两种情况下都表现出显著更高的静态微状态统计数据的主观方差。对于三种经典算法，解释方差最高，而对于HMM算法最低。HMM和PCA的分割显示出较低的熵和熵率。然而，拓扑结构的相似性在真实脑电数据和合成数据的结果中存在差异：对于静息状态脑电图，各种方法之间的拓扑结构总体上更相似，我们还可以观察到三种经典微状态算法与另外三种算法之间的差异。这种差异在合成数据中并不明显，准确度矩阵中的所有非对角线元素大致具有相同且相对较低的值。

6.替代数据

在研究中，我们进行了对替代数据的微状态分析。我们针对每个受试者的闭眼静息态脑电图数据，计算了多变量傅立叶变换（FT）替代数据（Theiler等，1992）。FT替代数据是一种随机化过程，其中原始数据被转换为傅立叶频谱域，其相位被随机化，然后具有随机傅立叶相位的数据被转换回时间域。此外，由于我们使用了FT过程的多变量版本，随机化在各通道间是相同的。这确保了替代数据具有与原始数据相同的协方差和时间自相关结构，但任何更高阶的（非线性）依赖关系都被破坏了。FT替代数据的微状态特性与原始闭眼静息态脑电图数据相当。这表明，协方差结构和时间自相关可能对这些观察到的微状态统计数据有很大的贡献。FT替代数据上的微状态分析的群体水平拓扑图与闭眼静息态脑电图数据相似，这表明协方差结构和相位主要决定了它们的随机化，保留了协方差。然而，微状态统计数据可能仍然有所不同，如图12所示。分割准确性与真实脑电图数据情况相似。然而，我们注意到，对于FT替代数据，只有AAHC和TAAHC表现出相互更高的准确性，而修改的K-Means与其他算法的准确性相似。然而，FT替代数据中的静态和广泛使用的微状态统计数据，如覆盖率、寿命和出现次数，都可以很好地由FT替代数据复制，呈现相同的模式：三种经典的微状态算法普遍一致，并且受试者间方差较低，而HMM和PCA具有较大的受试者间方差。总之，除了修改的K-Means在相互准确性方面存在轻微偏差外，所有其他微状态统计数据（静态和动态）似乎都可以很好地由真实闭眼静息态脑电图数据的FT替代数据复制。这表明协方差结构和时间自相关可能对这些观察到的微状态统计数据有很大的贡献。因此，结果表明可以从脑电图数据的协方差和时间自相关结构中估计微状态特性，而计算上要求高的微状态分解可能对估计这些特性并不是必要的。

图12. 在闭眼静息状态中，由LEMON数据集生成的傅里叶变换代理数据的潜在分割概述，子图意义同图11

7.自回归数据

假设微状态统计主要由协方差和自相关结构决定，拟合一个向量自回归（VAR）过程并生成一个加性高斯噪声的模拟应该产生相同的微状态统计数据。为此，我们设计了以下实验。首先，对于每个受试者，我们拟合了一个阶数为p的VAR过程，其中p∈[0，20]，并找到最小化Akaike信息准则的阶数。然后，我们对优化后的阶数p取中位数，以确定所有受试者的最佳阶数（对于p>5，AIC只有非常轻微的变化，我们认为最佳阶数为8，未显示）。其次，我们选择了数据段的长度，tseg∈[10，30，60，180]秒，对于所有受试者，我们使用改进的KMeans算法用于两个连续的静息状态脑电图数据段，用于模拟总长度tVAR= 3600秒，以及对于长VAR模拟的所有单独长度tseg（例如tseg= 10，数据为360段）。

在对这4种情况（两个连续的脑电图数据段、长VAR过程以及长VAR过程的各个数据段）进行微状态分解和统计计算后，我们评估了“预测误差”（即通过均方误差MSE来衡量的微状态统计估计之间的差异），包括第一个和第二个数据段之间的预测误差、VAR段的平均值和第二个数据段之间的预测误差，以及长VAR过程和第二个数据段之间的预测误差。最后，我们使用成对配对t检验比较了这三种情况下的预测误差（微状态属性估计中的MSE），即评估对比：数据预测误差 vs VAR段预测误差，数据预测误差 vs 完整VAR预测误差，以及完整VAR预测误差 vs VAR段预测误差。图13显示了VAR段预测误差和数据预测误差之间的对比的T值和p值。这两幅图展示了所有四种测试段长度的这些指标。正如图13清楚地显示的那样，大多数指标（除了熵率和解释方差）从VAR段中更好地“预测”出来，VAR过程可以生成与新数据段更接近的动态，至少在微状态统计的视角下，比以前的数据段更接近。这适用于所有长度的数据段。自然地，对于非常短的数据段（10秒），微状态估计的整体稳定性可能不会特别高。熵率和混合时间的测量对于短数据段长度（10和30秒）的VAR段估计非常准确。然而，对于更长的数据段（60和180秒），第一个数据段比VAR段更接近第二个数据段：对于更长的数据段长度，熵率和混合时间的估计更好，并趋于其理论值。总的来说，所有静态和一些动态微状态属性都可以通过VAR段的平均值得到正确的估计，这表明微状态属性和统计主要由协方差和时间自相关结构决定。

图13. VAR段微观状态估计与真实脑电图数据的比较，作为短片段均方误差的t检验。t检验是根据每个受试者第一和第二数据段之间的“预测误差”和每个受试者过程段和每个受试者第二数据段之间的“预测误差”平均值样本计算的。

讨论

这项研究通过在合成高斯数据上估计微状态特性，然后在真实脑电图（EEG）数据上估计微状态的地形和特性，详细研究了六种微状态算法。

通过计算GFP峰值对数据的时间减少的影响最小。唯一的例外是HMM算法（见图5）。重要的是，我们确实建议使用GFP峰值子采样，特别是对于经典的自下而上的微观状态聚类方法，即AAHC和TAAHC算法，因为它们如果没有直接并行化的选项，其计算要求非常高。

研究利用FT替代数据和VAR模型来测试微状态特性是否主要取决于基础EEG数据的线性结构。结果表明，除了熵率和解释方差之外，大多数测量在VAR段和真实EEG数据之间是可比较的。研究得出结论，所有静态和一些动态微状态特性都可以使用VAR段的总体平均值正确估计，这表明微状态特性和统计数据确实主要取决于基础EEG数据的协方差和时间自相关结构。此外，研究还质疑了微状态分析的必要性和优势，暗示与微状态特性相关的临床发现可能潜在地与EEG数据的线性特性相关，而无需进行计算密集的微状态分析。然而，微状态分析的实际优势可能在于其能够将EEG数据压缩为非常少的特征，提供EEG数据时空动态的低维表示。

结论

这项研究的主要目的是深入研究微状态分析的确切动态，以系统地比较文献中通常使用的各种算法。除了HMM外，其他5种选择的算法都得出了类似的结果，并没有显示出显著差异。大多数微状态特性纯粹由基础EEG信号的协方差和自相关结构决定；首先，通过生成EEG数据的多变量傅里叶变换替代物并进行微状态分析，其次，通过将向量自回归过程拟合到EEG数据中，从拟合的VAR过程中生成样本，并估计各种长度的VAR段上的微状态特性，发现大多数测量（除了熵率和解释方差）从VAR段处理的“预测”效果更好。

参考文献：Towards a dynamical understanding of microstate analysis of M/EEG data.