量子计算 21 量子算法 6 Shor Part III: QFT+PF
上回书介绍了QFT的量子电路,这其实是之前讲的Shor算法里面的第三步,我们今天来看第二步:
- 第一步,把质数分解问题,转化为周期寻找问题,这一步Shor认为是显然的,当然我们不会这么认为。。。
- 第二步,通过量子傅里叶变换QFT,以 O ( 1 ) O(1) O(1)查询复杂度解决周期寻找问题
- 第三步,建立QFT的量子电路,用 n O ( 1 ) = log n O ( 1 ) n^{O(1)}=\log n^{O(1)} nO(1)=lognO(1)个量子门
- 第四步,把冰箱门关上,用Continued Fraction Algorithm把QFT的输出变成质数分解的结果,然后大象就装冰箱里了
1 周期寻找量子态
第二步就是在我们已经有了QFT之后,用QFT作用之后的测量结果如何能解决周期寻找问题(Period finding QF)
已知我们的第一步在量子计算19中已经得到了周期寻找问题的相关量子态:
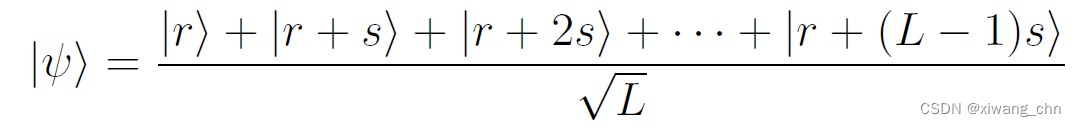
∣
ψ
⟩
|\psi\rangle
∣ψ⟩的这些分量,本来是
∣
0101
…
⟩
|0101\dots\rangle
∣0101…⟩形式的二进制,不过目前转化成了整数来表达,有
q
q
q个qubit,整数的范围也就是
0
∼
(
2
q
−
1
)
=
(
Q
−
1
)
0\sim (2^q-1)=(Q-1)
0∼(2q−1)=(Q−1);从向量的形式来看,其分量
∣
r
⟩
|r\rangle
∣r⟩也就是在第
r
r
r个位置上为1的单位向量。
2 QFT矩阵
我们的第三步已经在量子计算20中完成,即得到了QFT的快速量子电路,现在我们进行第二步,即将QFT作用于上述量子态。
QFT其实是以下矩阵
F
Q
F_Q
FQ:
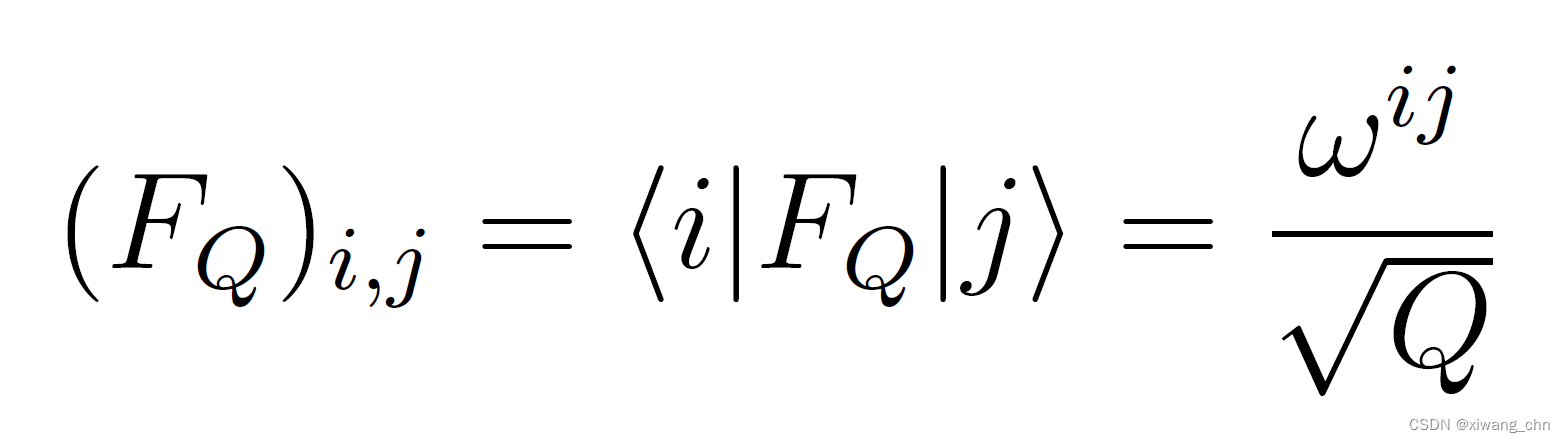
F
Q
F_Q
FQ是个
Q
×
Q
Q\times Q
Q×Q的矩阵,
Q
=
2
q
Q=2^q
Q=2q,
q
q
q是量子比特的数目;
w
i
j
=
e
2
π
i
/
Q
w^{ij}=e^{2\pi i/Q}
wij=e2πi/Q是单位1在复数范围的Q次方根。
3 QFT解决周期寻找问题
因此第二步就是
F
Q
∣
ψ
⟩
F_Q|\psi\rangle
FQ∣ψ⟩,根据上述分析,对于
∣
ψ
⟩
|\psi\rangle
∣ψ⟩中的第
l
l
l个分量
∣
r
+
l
s
⟩
|r+ls\rangle
∣r+ls⟩,
F
Q
∣
r
+
l
s
⟩
F_Q|r+ls\rangle
FQ∣r+ls⟩的结果相当于取矩阵
F
Q
F_Q
FQ的第
r
+
l
s
r+ls
r+ls行,因此
F
Q
∣
ψ
⟩
F_Q|\psi\rangle
FQ∣ψ⟩结果为:
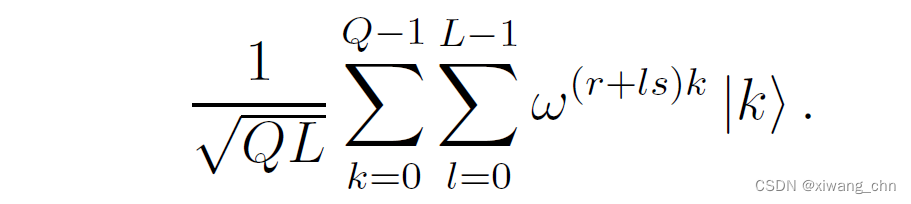
第一个求和,代表的是
F
Q
F_Q
FQ的第
r
+
l
s
r+ls
r+ls行共有
Q
Q
Q个分量;第二个求和,代表的是
∣
ψ
⟩
|\psi\rangle
∣ψ⟩共有
l
l
l个分量。
然后我们研究的问题就是,对于某个
∣
k
⟩
|k\rangle
∣k⟩,其幅值的相干是constructive interference还是destructive interference,为此我们可以先忽略其中的global phase
w
r
k
w^{rk}
wrk,因为对于特定的k是一样的,于是我们来看: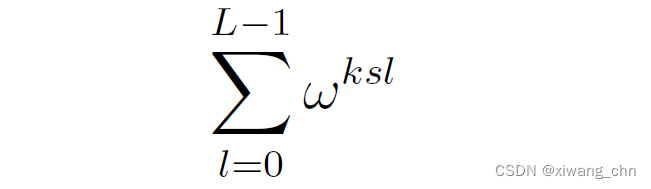
假如Q是s的整数倍
我们知道 w i j = e 2 π i / Q w^{ij}=e^{2\pi i/Q} wij=e2πi/Q
当
k
s
ks
ks不是Q的整数倍时,随着
l
l
l的增长,
k
s
l
m
o
d
Q
ksl \mod Q
kslmodQ会在
0
∼
Q
−
1
0\sim Q-1
0∼Q−1之间周期增长,反应到复数的单位圆上如下图,所以
L
L
L个这些周期复数加起来大多数就互相抵消了,所以就产生了destructive interference。
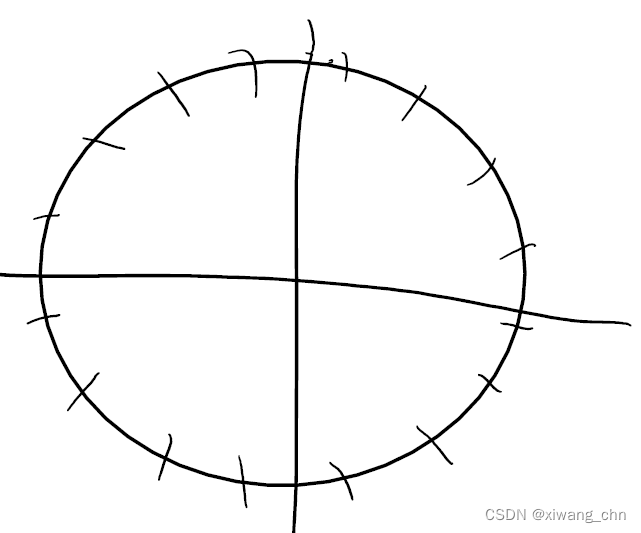
那当
k
s
ks
ks是Q的整数倍的时候,
w
k
s
l
=
1
w^{ksl}=1
wksl=1,因此这样的
∣
k
⟩
|k\rangle
∣k⟩的幅值,在
l
l
l个求和之后,是发生了constructive interference的。
所以大概率上,我们观测到的 ∣ k ⟩ |k\rangle ∣k⟩,对某整数 c c c,满足 k s = c Q ⟺ k = c Q s ks=cQ\iff k=c\frac{Q}{s} ks=cQ⟺k=csQ,所以我们经过多次运行量子电路可以获得多个: c 1 Q s , c 2 Q s , … c T Q s c_1\frac{Q}{s}, c_2\frac{Q}{s}, \dots c_T\frac{Q}{s} c1sQ,c2sQ,…cTsQ,因此计算他们的最大公约数,在T很小的情况下,就能很大概率上获得我们想要的周期 s s s。
假如Q不是s的整数倍
假设对于量子态分量 ∣ k ⟩ |k\rangle ∣k⟩,有 k = c Q s + Δ k=c\frac{Q}{s}+\Delta k=csQ+Δ,则当 Δ \Delta Δ越小,其被观测的结果越大,接下来分析: ∑ l = 0 L − 1 w k s l = ∑ l = 0 L − 1 e 2 π i k s l / Q = ∑ l = 0 L − 1 e 2 π i ( c Q s + Δ ) s l / Q = ∑ l = 0 L − 1 e 2 π i Δ s l / Q \sum_{l=0}^{L-1}w^{ksl}=\sum_{l=0}^{L-1} e^{2\pi iksl/Q}=\sum_{l=0}^{L-1} e^{2\pi i(c\frac{Q}{s}+\Delta)sl/Q}=\sum_{l=0}^{L-1} e^{2\pi i \Delta sl/Q} ∑l=0L−1wksl=∑l=0L−1e2πiksl/Q=∑l=0L−1e2πi(csQ+Δ)sl/Q=∑l=0L−1e2πiΔsl/Q
因此,当
Δ
\Delta
Δ很小的时候,当
l
l
l在
0
∼
L
−
1
0\sim L-1
0∼L−1变化时,在复数单位圆上的变化如图,这种时候是方向相近的向量叠加,发生了constructive interference;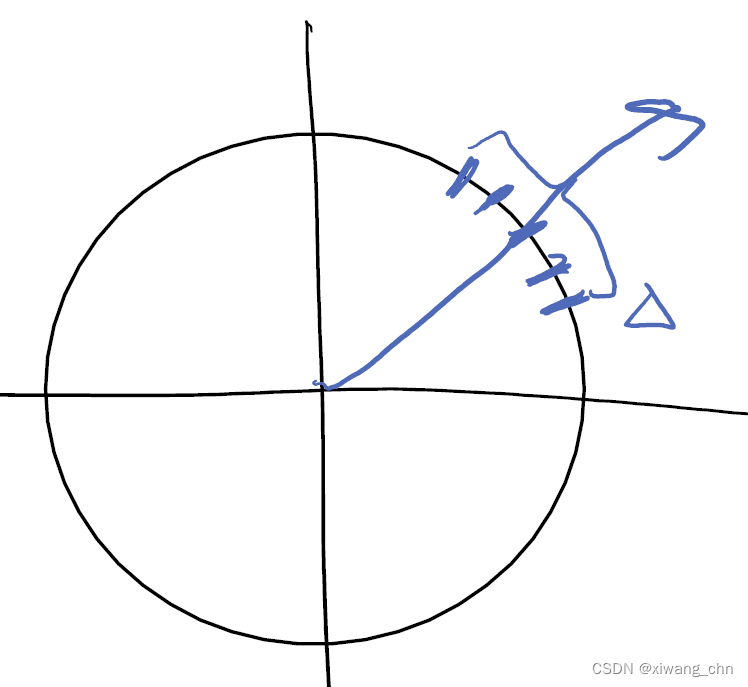
反之,当
Δ
\Delta
Δ较大时候,不同的向量方向差异较大,就会产生周期变化互相抵消,产生destructive interference,因为我们知道
L
≈
Q
s
L\approx \frac{Q}{s}
L≈sQ,所以
Δ
\Delta
Δ接近1的时候这些量子幅就相当于分布在单位圆周围一圈了,如果再小上几倍,比如小10倍,其实就变成了相当的constructive interference。
所以,很高概率上,我们观察到的
k
=
c
Q
s
+
Δ
k=c\frac{Q}{s}+\Delta
k=csQ+Δ,是非常接近某个整数
c
Q
s
c\frac{Q}{s}
csQ的,其概率分布图如下:
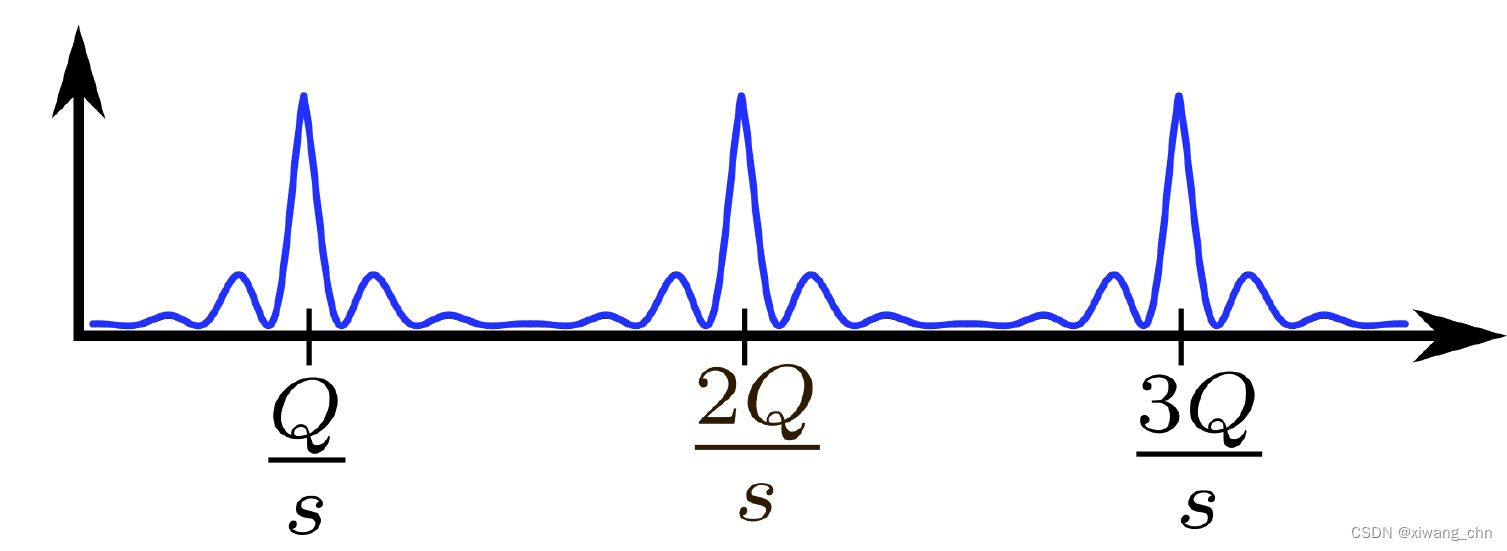
因此,
k
=
c
Q
s
+
Δ
⟺
k
Q
=
c
s
+
Δ
Q
⟺
∣
k
Q
−
c
s
∣
=
Δ
Q
k=c\frac{Q}{s}+\Delta\iff \frac{k}{Q}=\frac{c}{s}+\frac{\Delta}{Q}\iff |\frac{k}{Q}-\frac{c}{s}|=\frac{\Delta}{Q}
k=csQ+Δ⟺Qk=sc+QΔ⟺∣Qk−sc∣=QΔ,所以
∣
k
Q
−
c
s
∣
=
Δ
Q
|\frac{k}{Q}-\frac{c}{s}|=\frac{\Delta}{Q}
∣Qk−sc∣=QΔ是很小的
(
∼
1
Q
)
(\sim \frac{1}{Q})
(∼Q1),我们已知观测到的
k
k
k和
q
q
q个qubit (
Q
=
2
q
Q=2^q
Q=2q),不知道的是
c
c
c和
s
s
s,仅仅知道他们都是整数,且
s
<
<
Q
s<<\sqrt{Q}
s<<Q。
怎么求解 c c c和 s s s呢?请见下回Continued Fractions!






















 1555
1555











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








