量子计算（11）量子算法1：可逆线路

计算机鬼才～

已于 2023-05-15 13:57:01 修改

阅读量526

点赞数 3

分类专栏：量子计算文章标签：量子计算

于 2023-03-13 00:27:16 首次发布

本文链接：https://blog.csdn.net/m0_69299019/article/details/129477828

版权

量子计算专栏收录该内容

13 篇文章 58 订阅

订阅专栏

哈喽哈喽大家好呀！又到了一周一度小编分享量子计算的时刻啦！几天不见，大家是不是甚是想念小编呢。之前答应大家的，本周要开始进入量子算法的学习。提到算法，大家会想到什么？是深度优先算法？哈夫曼编码算法？排序算法？梯度下降法？还是说动态规划法？二分法？KMP算法？诸如此类，但是这些都是我们针对经典量子比特而设计出来的算法。那么，我们学习了这么多次量子计算的课程，有没有什么针对量子比特的算法呢？

诶嘿，您还别说，还真有一些国内外大佬想出来的量子计算的算法，虽然目前量子计算的算法还没有完全开发完，也就是说，量子计算领域还有很多种人类并没有想出来的算法，但是目前想出来的一些算法，确实很厉害，相较于经典算法快了不少。

一、可逆电路

我们知道，处理量子信息的基本单元是量子逻辑门，量子信息经过各个量子逻辑门时，依据门功能发生变换，量子逻辑门对量子信息的操作其实就是一个酉变换，酉变换的一个重要特点就是这些酉变换都是可逆的，即每个量子逻辑门也是可逆的。

比如说H门，我们证明一下，它是酉变换：

首先，酉矩阵满足 $U^{\dagger }=(\overline{U})^{T}$ 以及 $U^{\dagger }\cdot U=I_{n}$ 。

而H门对应的矩阵为H= $\frac{1}{\sqrt{2}}\begin{pmatrix} 1 &1 \\ 1& -1 \end{pmatrix}$ ，那么它的伴随为 $H^{\dagger }=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 &1 \\ 1& -1 \end{pmatrix}$ ，经计算，发现它满足 $H\cdot H^{\dagger }=I_{n}$ 。

同理，我们也可以一一验证X门、Y门、Z门以及众多的多量子逻辑门，都是酉变换。

我们在量子电路中，不可能只用一个量子门，对吧。那么我们还需要证明：酉矩阵乘酉矩阵仍然是一个酉矩阵。

设U1、U2均为个酉矩阵，那么我们有 $U_{1}^{\dagger }=(\overline{U_{1}})^{T}$ ， $U_{2}^{\dagger }=(\overline{U_{2}})^{T}$ ，那么 $U_{1}^{\dagger }\cdot U_{2}^{\dagger }=(\overline{U_{1}})^{T}\cdot (\overline{U_{2}})^{T}$ 。又因为 $A^{T}\cdot B^{T}=(BA)^{T}$ ，所以 $U_{1}^{\dagger }\cdot U_{2}^{\dagger }=(\overline{U_{2}}\cdot \overline{U_{1}})^{T}$ 。而 $\overline{A}\cdot \overline{B}=\overline{BA}$ ，所以 $U_{1}^{\dagger }\cdot U_{2}^{\dagger }=(\overline{U_{1}\cdot U_{2}})^{T}$ ，满足酉矩阵的第一条性质。而 $U_{1}^{\dagger }\cdot U_{1}=I_{n}$ ， $U_{2}^{\dagger }\cdot U_{2}=I_{n}$ ，那么 $(U1U_{2})^{\dagger }\cdot (U_{1}U_{2})=(\overline{U_{1}\cdot U_{2}})^{T}\cdot (U_{1}\cdot U_{2})$ ，继续拆解括号里的内容有 $(U1U_{2})^{\dagger }\cdot (U_{1}U_{2})=(U_{2}^{\dagger }\cdot U_{1}^{\dagger })\cdot (U_{1}\cdot U_{2})$ ，矩阵乘法具有结合性，所以最终有 $(U1U_{2})^{\dagger }\cdot (U_{1}U_{2})=I_{n}\cdot I_{n}=I_{n}$ 。

因此，我们得出结论：量子电路由若干量子逻辑门级联构成，它是对量子信息作一系列酉变换以实现电路功能，而酉变换一定是可逆的，所以当我们设计电子线路与电子算法时，一定要考虑可逆的相关性质，小编总结如下。

量子可逆逻辑电路具有以下特点：①输入线路与输出线路相等，而且满足函数是单射与满射的，即shuang射（CSDN挺奇怪的，不让我打出来这个词语）；②没有反馈线路；③电路分层级联，有时为了保证电路可逆性需要人为添加一些辅助位，即没有用的数据位。

那么我们需要了解一下shuang射是什么，这个其实是高中的知识，小编带大家温习一下：在集合论中，一个由集合X至集合Y的映射称为双射的，若对集合Y内的任意元素y，存在唯一一个集合X内的元素x，使得 y = f(x)。换句话说，f为双射的若其为两集合间的一对一对应，亦即同时单射且满射。

一个n位输入、n位输出的量子线路，称为n×n规模的量子电路。

二、设计电路

刚刚我们说到，量子线路是可逆线路，不过可惜的是，对于经典比特中的各种门，大多数都不是可逆的，下面我们将一一判别一下，并且带领大家“改造”这些经典电路门。

1、非门NOT

何谓非门？非门（英语：NOT gate）又称反相器（英语：Inverter），是数字逻辑中实现逻辑非的逻辑门，功能见如下真值表：

输入A	输出f（A）
1	0
0	1

我们发现它完全满足可逆条件，既是满射，也是单射。而且我们还知道，在量子线路中用一个X门就能完成对非门的转换。

2、与门AND

与门(英语:AND gate)又称"与电路"、逻辑"积"、逻辑"与"电路。是执行"与"运算的基本逻辑门电路。有多个输入端，一个输出端。当所有的输入同时为高电平(逻辑1)时，输出才为高电平，否则输出为低电平(逻辑0)。其真值表为：

输入1	输入2	输出
0	0	0
0	1	0
1	0	0
1	1	1

很明显，输入数量与输出数量都不一致，更别说满足可逆条件了。我们需要对这个电路好好的“改造”一下，让它脱胎换骨！

在经典电路中，我们用如下的方式，让它变得输入与输出一一对应。一般情况下，如果y=f（i）有n个输入与m个输出，我们改造的时候，会额外添加与原输出数量一致的输入以及与原输入数量一致的输出。也就是说增加m个输入以及n个输出。然后新增的输出值与原来的输入值一致，但是函数的输出需要变成未改造前的输出异或新添加的输入值。语言上很难理解，但是看下面这个例子大家就立马会了。

在与门中，对应刚刚的改造方法，我们要添加一个输入与两个输出。并且原来的输出要改造成ab的“与”操作，然后与c异或的结果。这样子能满足一一对应，而且还能完美的满足单射与满射。如图右侧的真值表所示。

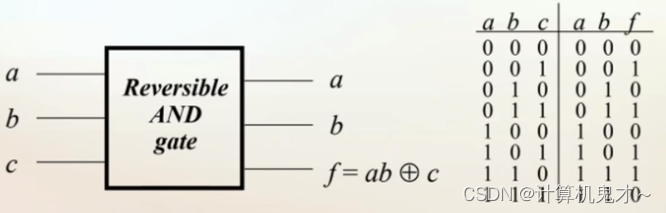
紧接着，请大家思考一下，这个电路怎么设计。不知道大家还记不记得Toffoli门，当前两个量子比特位1的时候，翻转第三量子比特。诶嘿？这乍一看，不就是Toffoli门能完成的操作吗？而且我们只需要控制c为|0>态，就能得到与操作后真正的值。

那么依据前几篇文章的知识，我们是不是能够用pyqpanda实现“量子与门”操作？请大家动动手，和小编一起完成编程。

from pyqpanda import  *

def get_number():
    a=int(input("请输入输入的值"))
    return a
//输入输入1与输入2的值


if __name__ == "__main__":
    a=get_number()
    b=get_number()

    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(3)
    cbits = qvm.cAlloc_many(3)
    cbits[2].set_val(b)
    cbits[1].set_val(a)
    branch0 = QProg()
    branch1 = QProg()
    branch2 = QProg()

    prog=QProg()
    prog1=QProg()
    branch1.insert(X(qubits[1]))//branch1用于当输入1为1时，使该线路由|0>变为|1>
    branch2.insert(X(qubits[2]))//与楼上同理
    prog1.insert(Toffoli(qubits[2],qubits[1],qubits[0]))//执行TOFFOLI门操作
    qif1=QIfProg(cbits[1]==1,branch1,branch0)
    qif2=QIfProg(cbits[2]==1,branch2,branch0)
    measure=Measure(qubits[0], cbits[0])
    prog.insert(qif1)
    prog.insert(qif2)
    prog.insert(prog1)
    prog.insert(measure)


    result1 = qvm.prob_run_dict(prog, qubits, -1)

    # 打印概率测量结果
    print(result1)

结果如下图：