优化算法综述
| 依据 | 分类 | 具体算法 |
| 1 | 全局优化 | 遗传算法(GA)、帝国竞争算法(ICA)、 粒子群优化(PSO) |
| 局部优化 | 模拟退火(SA)、贪婪算法(Greedy)、 邻域搜索(NS) | |
| 2 | 精确算法 | 线性规划(LP)、分支定界法(BB) |
| 模拟进化算法 | v | |
| 群体仿生类算法、又称为群体智能优化算法 | GA、PSO | |
| 数学规划方法: | 动态规划(DP)、线性规划、整数规划、 混合整数规划、 分支定界法、 割平面法 | |
| v | ||
| v | ||
| 启发式算法(Heuristic Algorithms) | v | |
| 元启发式算法(Meta-Heuristic Algorithms) | v |
数学规划法
数学规划法:通常将多目标问题转化为单目标问题来解决。
精确算法(exact algorithm)
精确算法:通常将待解决的优化问题转换为数学规划问题,进行精确求解。如:分支定界法(BB)。
- 优点:在问题规模较小时,精确算法能在合理的时间内找到问题的最优解;
- 缺点:但当问题规模较大时(是NP-Hard问题),精确算法的计算复杂度高,求解时间呈指数级增长,不能容忍(指数爆炸)。
启发式 VS. 元启发式
问题描述:现实中很多问题的优化都可以建模为基于序列的组合优化,如旅行商问题(TSP)、排产问题、各类资源分配问题等。寻找最优序列的问题是NP难问题(NP-Hard问题)(其解空间为n!)。
解决这类问题常用的方法有两种:
- (1)一种方法是启发式算法,启发式算法是基于问题本身的规则得到较好的可行解,本质是贪心算法(贪婪算法,greedy)。这种方法速度较快,但因与问题本身联系紧密(problem specific, problem dependent),导致其通用性较差。
- (2)另一种方法是元启发式算法,例如遗传算法、禁忌搜索算法、蚁群算法、模拟退火算法等都是元启发式算法。这类方法从生物进化、物理、化学等过程中受到启发,得到一种解空间的搜索策略,因其搜索策略独立于问题本身(problem independent),因此通用性强。元启发式这类算法有两个最本质的操作:①选择操作(从当前种群中选出优秀的个体,选择的策略有精英保留、轮盘赌、锦标赛等);②改变操作(如交叉、变异、灾变操作等,它们本质上都是从一个可行解改变为另一个可行解,用来扩大搜索范围,避免陷入局部最优)。(详见:元启发式算法常用操作详解:https://bbs.huaweicloud.com/blogs/195717)
启发式算法
启发式策略(heuristic)是一类在求解某个具体问题时,在可以接受的时间和空间内能给出其可行解(或近优解),但又不保证求得最优解(以及可行解与最优解的偏离)的策略的总称。
许多启发式算法是相当特殊的,它依赖于某个特定问题。启发式策略在一个寻求最优解的过程中能够根据个体或者全局的经验来改变其搜索路径,当寻求问题的最优解变得不可能或者很难完成时(e.g. NP-C问题),启发式策略就是一个高效的获得可行解(即近优解)的办法。
启发式算法包括:包括构造型方法、局部搜索算法、松弛方法、解空间缩减算法、贪婪策略、随机化贪婪策略、近邻策略、最大饱和度策略等。
元启发式算法
元启发式策略(Meta-heuristic)则不同,元启发式策略通常是一个通用的启发式策略,它们通常不借助于某种问题的特有条件,从而能够运用于更广泛的方面。元启发式是启发式策略的增强改进版,它是随机算法与局部搜索算法相结合的产物。“元”可以理解为一个哲学概念,大概是“事物的本原”。
元启发式策略通常会对搜索过程提出一些要求,然后按照这些要求实现的启发式算法便被称为元启发式算法。许多元启发式算法都从自然界的一些随机现象取得灵感(e.g. 模拟退火、遗传算法、粒子群算法)。现在元启发式算法的重要研究方向在于防止搜索过早得陷入局部最优,已经有很多人做了相应的工作,例如禁忌搜索(tabu)和非改进转移(模拟退火)。
元启发式算法是相对于最优化算法提出来的,一个问题的最优化算法可以求得该问题的最优解,而元启发式算法是一个基于直观或经验构造的算法,它可以在可接受的花费(指计算时间和空间)下给出问题的一个可行解(近优解),并且该可行解与最优解的偏离程度不一定可以事先预计。
元启发式算法(Meta-heuristic)是基于计算智能的机制求解复杂优化问题最优解或满意解(近优解)的方法,有时也被称为智能优化算法(Intelligent optimization algorithm),智能优化通过对生物、物理、化学、社会、艺术等系统或领域中相关行为、功能、经验、规则、作用机理的认识,揭示优化算法的设计原理,在特定问题特征的引导下提炼相应的特征模型,设计智能化的迭代搜索型优化算法。
常见的Meta-Heuristic Algorithms(有基于个体和基于群体两类):
一、基于个体(Single solution-based heuristics)
1、模拟退火(Simulated Annealing,SA)
2、禁忌搜索(Tabu Search,TS)
3、变邻域搜索(Variable Neighborhood Search)
4、自适应大规模领域搜索(Adaptive Large Neighborhood Search)
二、基于群体(Population-based heuristics)
1、遗传算法(Genetic Algorithm,GA)
2、蚁群优化算法(Ant Colony Optimization,ACO)
3、粒子群优化算法(Particle Swarm Optimization,PSO)
4、差分进化算法(Differential Evolution, DE)
4、人工蜂群算法(ABC)、人工鱼群算法、狼群算法等
5、人工神经网络算法(ANN)
另外还有:免疫算法、蛙跳算法、帝国竞争算法(Imperialist Competitive Algorithm,ICA)、和声搜索算法、分布估计算法、Memetic算法、文化算法、灰狼优化算法、人工免疫算法、进化规划、进化策略、候鸟优化算法、布谷鸟搜索算法、花朵授粉算法、引力搜索算法、化学反应优化算法、头脑风暴优化算法(Brain Storm Optimization Algorithm,BSO)等等。
附:元启发式算法时间表(部分)

What is the difference between heuristics and meta-heuristics?
- 启发式算法和元启发式算法,一般都是用来解决NP-H问题,目的是求得组合优化问题的近优解(可行解、满意解),但不一定是最优解。【它们和最优化算法相对应,最优化算法是用来求得问题的最优解的。】
- 启发式算法是 problem dependent(依赖于问题的,与问题有关)或者叫 problem specific(面向特定问题的,与特定问题有关),故适应面窄; 而元启发式算法是problem independent(与问题无关的),元启发法是与问题无关的技术,可以应用于广泛的问题,适用范围广。
- 启发式方法利用问题相关信息来找到特定问题的"足够好"的解决方案,根据给定问题制定启发式规则,故与该问题特性有关;而元启发式方法则像设计模式一样,是一般的算法思想,可以应用于各种各样的问题,与问题无关。
- 复杂性方面,启发式算法简单,就是用简单策略(如:贪婪策略、随机化贪婪策略、近邻策略、最大饱和度策略)构造可行集的过程。而元启发式则是一种高层次的多个算法模块的聚合算法。
有段英文可以读读,理解一下:
A locally optimal solution is better than all neighbouring solutions. A globally optimal solution is better than all solutions in the search space. A neighbourhood is a set of solutions that can be reached from the current solution by a simple operator. A neighbourhood is a subset of the search space. (局部最优解、全局最优解与邻域的概念)
A heuristic is a rule of thumb method derived from human intuitions. For example, we can use the nearest neighbour heuristic to solve the TSP problem and use the maximal saturation degree heuristic to solve the graph colouring problem.(其次,我们可以利用启发式算法搜索并得到一个局部最优解(不保证是全局最优解))
Meta-heuristics are methods that orchestrate an interaction between local improvement procedures and higher-level strategies to create a process capable of escaping from the local optima and performing a robust search in the solution space. Single-point meta-heuristics include Simulated Annealing, Tabu Search, and Variable Neighbourhood Search. Population-based meta-heuristics include Genetic Algorithm, Ant Colony Optimization, and Particle Swarm Optimization.(最后,我们可以利用元启发式算法更好地探索解空间,从而避免算法陷入局部最优)
多目标智能优化算法
多目标进化算法(Multi-Objective Evolutionary Algorithm,MOEA),如:增强多目标灰狼优化算法、多目标粒子群优化算法、多目标遗传算法、NSGA-Ⅱ算法(即带有精英保留策略的快速非支配多目标优化算法,是一种基于Pareto最优解的多目标优化算法,是多目标遗传算法的一种)。
多目标优化算法,它主要针对同时优化多个目标(两个及两个以上)的优化问题,这方面比较经典的算法有NSGAII算法、MOEA/D算法以及人工免疫算法等。这部分内容的介绍已经在博客《[Evolutionary Algorithm] 进化算法简介》进行了概要式的介绍,有兴趣的博友可以进行参考(2015.12.13)-Poll的笔记。
模拟进化算法与传统的精确算法(确定性算法)的区别
- 模拟进化算法的作用对象是由多个可行解组成的集合(种群),而非单个可行解;
- 模拟进化算法只利用目标函数(或适应度函数)的适应值信息(fitness value),而无需使用梯度等其它辅助信息;
- 模拟进化算法利用概率机制,非确定性迭代过程描述。
- 正是这些有别于确定型方法的特征,决定了模拟进化算法应用的广泛性、描述的简单性、本质上的并行性及良好的鲁棒性。
优化算法分类
- 启发式优化算法:一个基于直观或经验构造的算法,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解,该可行解与最优解的偏离程度不一定事先可以预计.意思就是说,启发式算法是根据经验或者某些规则来解决问题,它求得的问题的解不一定是最优解,很有可能是近似解(或近优解)。这个解与最优解近似到什么程度,是不能确定的。相对于启发式算法,最优化算法或者精确算法(比如说分支定界法、动态规划法等则能求得最优解)。而元启发式优化算法(Meta-heuristic Algo.)是启发式算法中比较通用的一种高级一点的算法,主要有遗传算法、禁忌搜索算法、模拟退火算法、蚁群算法、粒子群算法、变邻域搜索算法、人工神经网络、人工免疫算法、差分进化算法等。这些算法可以在合理的计算资源条件下给出较高质量的解(最优解或近优解)。
- 仿生算法:基于仿生学的算法,是一类模拟自然生物进化或者群体社会行为的随机搜索方法的统称.由于这些算法求解时不依赖于梯度信息,故其应用范围较广,特别适用于传统方法难以解决的大规模复杂优化问题.主要有:遗传算法、人工神经网络、蚁群算法、蛙跳算法、粒子群优化算法等.这些算法均是模仿生物进化、神经网络系统、蚂蚁寻路、鸟群觅食等生物行为,故叫仿生算法。
- 智能计算:也称为计算智能,群体智能算法。包括遗传算法、模拟退火算法、禁忌搜索算法、进化算法、蚁群算法、人工鱼群算法,粒子群算法、混合智能算法、免疫算法、神经网络、机器学习、生物计算、DNA计算、量子计算、模糊逻辑、模式识别、知识发现、数据挖掘等.智能计算是以数据为基础,通过训练建立联系,然后进行问题求解.
所以说,你接触的很多算法,既是仿生算法,又是启发式算法,又是智能算法,这都对!只是分类方法不同而已。
算法介绍
帝国竞争算法(Imperialist Competitive Algorithm,ICA)
帝国竞争算法(ICA)是Atashpaz-Gargari和Lucas于2007年提出的一种基于帝国主义殖民竞争机制的进化算法,属于社会启发的随机优化搜索方法。目前,ICA已被成功应用于多种优化问题中,如调度问题、分类问题和机械设计问题等。
帝国主义竞争算法,借鉴了人类历史上政治社会殖民阶段帝国主义国家之间的竞争、占领、吞并殖民殖民地国家从而成为帝国国家的演化,是一种全局性的优化算法。该算法把所有初始化的个体都称作国家,按照国家势力分成帝国主义国家及殖民地两种,前者优势大于后者。
其实,从另一个角度来看,ICA可以被认为是遗传算法(GA)的社会对应物。ICA是基于人类社会进化的过程,而GA是基于物种的生物进化过程。二者其实有异曲同工之妙。
不过话说回来,大多数群体仿生类算法都有异曲同工之妙。
分支定界法(Branch and Bound, BB)
For instance, since the space of possible solutions is still too vast, a branch and bound type algorithm is proposed to further decimate the number of potential solutions to evaluate.
例如,由于可行解的参数空间很大,一种分支限界算法被用来减少需要考察的可行解的数目。
Branch and bound (BB or B&B) is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as general real valued problems. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
NSGA-Ⅱ算法
NSGA(Non-dominated Sorting Genetic Algorithm,非支配排序遗传算法)、NSGA-II(带精英策略的快速非支配排序遗传算法),都是基于遗传算法的多目标优化算法,是基于pareto最优解讨论的多目标优化。
NSGA-Ⅱ算法,即带有精英保留策略的快速非支配多目标优化算法,是一种基于Pareto最优解的多目标优化算法。
NSGA-Ⅱ算法是进化算法中的一种,进化算法是在遗传算法的基础上改进而来的,所以,你得先弄懂遗传算法是什么。
NSGA-Ⅱ是最流行的多目标遗传算法之一,它降低了非劣排序遗传算法的复杂性,具有运行速度快,解集的收敛性好的优点,成为其他多目标优化算法性能的基准。
NSGA-Ⅱ算法是 Srinivas 和 Deb 于 2000 年在 NSGA 的基础上提出的,它比 NSGA算法更加优越:它采用了快速非支配排序算法,计算复杂度比 NSGA 大大的降低;采用了拥挤度和拥挤度比较算子,代替了需要指定的共享半径 shareQ,并在快速排序后的同级比较中作为胜出标准,使准 Pareto 域中的个体能扩展到整个 Pareto 域,并均匀分布,保持了种群的多样性;引入了精英策略,扩大了采样空间,防止最佳个体的丢失,提高了算法的运算速度和鲁棒性。
NSGA-Ⅱ就是在第一代非支配排序遗传算法的基础上改进而来,其改进主要是针对如上所述的三个方面:
- 提出了快速非支配排序算法,一方面降低了计算的复杂度,另一方面它将父代种群跟子代种群进行合并,使得下一代的种群从双倍的空间中进行选取,从而保留了最为优秀的所有个体;
- 引进精英策略,保证某些优良的种群个体在进化过程中不会被丢弃,从而提高了优化结果的精度;
- 采用拥挤度和拥挤度比较算子,不但克服了NSGA中需要人为指定共享参数的缺陷,而且将其作为种群中个体间的比较标准,使得准Pareto域中的个体能均匀地扩展到整个Pareto域,保证了种群的多样性。
这个算法是本人接触科研学习实现的第一个算法,因此想在这里和大家分享一下心得。 讲解的很详细,读个大概,有个思路和印象即可,不必深究。
site:https://blog.csdn.net/qq_40434430/article/details/82876572/
遗传算法(Genetic Algorithm, GA)
遗传算法(Genetic Algorithm,简称GA)是一种最基本的进化算法,它是模拟达尔文生物进化理论的一种优化模型,最早由J.Holland教授于1975年提出。
遗传算法中种群分每个个体都是解空间上的一个可行解,通过模拟生物的进化过程,从而在解空间内搜索最优解。
禁忌搜索算法(Tabu Search,TS)
遗传算法是具有全局搜索能力的算法,但是传统遗传算法求解调度问题并不是很成功,主要原因在于它的局部搜索能力较差,且容易早熟收敛。而禁忌搜索(Tabu Search, TS)是一种优秀的局部搜索算法。因此,可以结合遗传算法(GA)和禁忌搜索算法(TS)两者的优点,将“适者生存”的遗传准则嵌入到多起点的禁忌搜索算法中,构成混合遗传禁忌搜索算法(GATS)。
由于遗传算法和禁忌搜索算法具有互补的特性,因此混合遗传禁忌搜索算法(GATS)在性能上能够超越它们单独使用时的性能。
文化基因算法(Memetic Algorithm,MA)
文化基因(Meme)的概念是由Hawkins于1976年提出的,Pablo Moscato于1989年提出了Memetic Algorithm。Memetic Algorithm,是基于群体的计算智能方法与局部搜索相结合的一类算法的总称。文化基因算法的简单介绍。

文化基因算法(Memetic Algorithm,简称MA),也被称为是“密母算法”(Meme),它是由Moscato在1989年提出的。文化基因算法MA是一种基于种群的全局搜索和基于个体的局部启发式搜索的结合体,它的本质可以理解为:
MA= GA + Local Search
即MA算法实质上是为遗传算法(全局搜索算法)加上一个局部搜索(Local Search)算子。局部搜索算子可以根据不同的策略进行设计,比如常用的爬山机制、模拟退火、贪婪机制、禁忌搜索等。

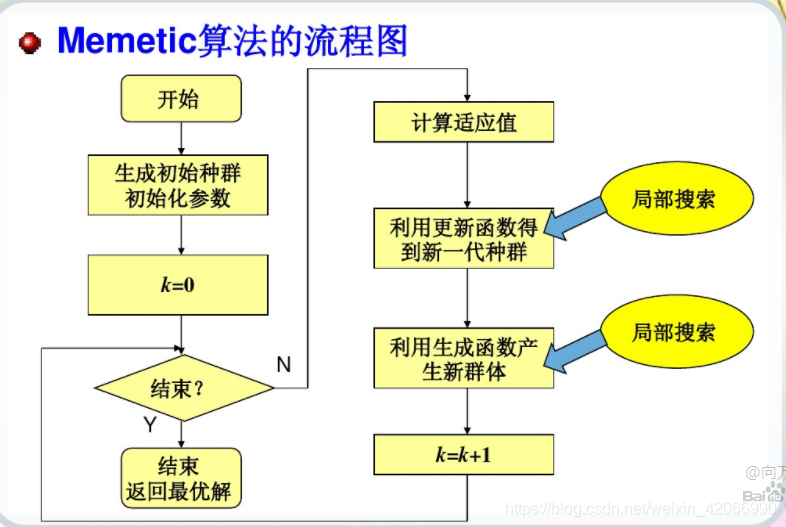
Pablo Moscato认为:在遗传算法(GA)中,变异操作可以看作是含有一定噪声的爬山搜索,实际上模拟遗传编码和自然选择的过程不应包含变异操作,因为在文化进化的过程中,在众多的随机变化步骤中得到一个正确的、可提高整体性能的一步进展是非常困难的,只有此领域的拥有足够的专业知识的精通者们,才有可能创造新的进展,并且这样的事情发生的频率是很低的。 因此,文化基因的传播过程应是严格复制的,若要发生变异,那么每一步的变异都需要有大量的专业知识支撑,而每一步的变异都应带来进展而不是混乱,这就是为什么我们观察到的文化进化速度要比生物进化速度快得多的原因。 对应于模拟生物进化过程的遗传算法,Moscato提出了模拟文化进化过程的文化基因算法,文化基因算法用局部启发式搜索来模拟由大量专业知识支撑的变异过程。因此说,文化基因算法是一种基于种群的全局搜索和基于个体的局部启发式搜索的结合体。
文化基因算法的这种全局搜索和局部搜索的结合机制,使其搜索效率在某些问题领域比传统遗传算法快几个数量级,可应用于广泛的问题领域并得到满意的结果。 很多人将文化基因算法看作混合遗传算法、 遗传局部搜索或是拉马克式进化算法。实际上,文化基因算法提出的只是一种框架、 是一个概念,在这个框架下,采用不同的搜索策略可以构成不同的文化基因算法。如全局搜索策略可以采用遗传算法、 进化策略、 进化规划等,局部搜索策略可以采用爬山搜索、模拟退火、贪婪算法、禁忌搜索、导引式局部搜索等。 这种全局与局部的混合搜索机制显然要比单纯在普通个体间搜索的进化效率高得多。
机器学习中的最优化模型
我们每个人都会在我们的生活或者工作中遇到各种各样的最优化问题,比如每个企业和个人都要考虑的一个问题“在一定成本下,如何使利润最大化”等。最优化方法是一种数学方法,它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。随着学习的深入,博主越来越发现最优化方法的重要性,学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解,比如我们现在学习的机器学习算法,大部分的机器学习算法的本质都是建立优化模型,通过最优化方法对目标函数(或损失函数)进行优化,从而训练出最好的模型。常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度法、最速下降法等等。







 本文全面概述优化算法,包括数学规划法、精确算法、启发式与元启发式策略。元启发式算法如遗传算法、禁忌搜索、模拟退火等在解决复杂优化问题时展现出强大能力,其通用性和跳出局部最优的能力使其成为研究热点。此外,介绍了帝国竞争算法、分支定界法、NSGA-Ⅱ等具体算法,以及机器学习中的最优化模型如梯度下降、牛顿法等。
本文全面概述优化算法,包括数学规划法、精确算法、启发式与元启发式策略。元启发式算法如遗传算法、禁忌搜索、模拟退火等在解决复杂优化问题时展现出强大能力,其通用性和跳出局部最优的能力使其成为研究热点。此外,介绍了帝国竞争算法、分支定界法、NSGA-Ⅱ等具体算法,以及机器学习中的最优化模型如梯度下降、牛顿法等。

















 1917
1917










