2023年五一数学建模 B 题过程与结果

第一问

见 2023 年 五一杯 B 题过程 + 代码（第一问）

第二问

第二问考虑是一个时序预测问题，采用 ARIMA 模型即可

数据时序分析

对于 每一个路径，快递数时间序列，以路径 G->L 为例，其取值如下所示：

根据 ADF 检验，分析出路径 G->L 是否为稳定序列。根据 ADF 假设检验结果，由于ADF检验的 p值为： 0.002 检验统计量 ADF 为： -3.87。由于 p 值小于置信水平 0.05，因此可以认为时间序列是平稳的。

因此，采用 ARIMA(p,d,q)模型时，差分系数应为 d = 0。如果 ADF 检验的 p 值小于 0.05，则说明差分后的序列是平稳的。否则需要继续进行差分。此时差分系数 d 等于差分直至时序数据平稳时的差分次数。

绘制时序数据的自相关图，和偏自相关图，如下：


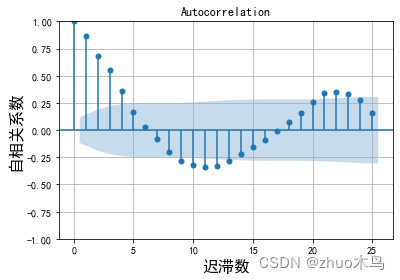
从图中可以得出，ARIMA 模型的自回归系数为 p=5（自相关系数截尾），移动平均系数 q=1(偏相关系数均衡衰减，取较小值 q)。

Auto-ARIMA

通过偏自相关系数图、自相关系数图筛选 p，q 带有主观性。因此结合 AIC 评价指标，将数据分为测试集和验证集，从而在众多（p，q）参数的组合中，筛选出最佳的 p，q 并与 ADF 检验确定的 d 值，从而得出最佳的 ARIMA 模型。

具体流程为：

1. 对每一个路径，绘制偏自相关系数、自相关系数图，筛选 p，q 的最大取值 $p_{max},q_{max}$。如上例 G-> L 路径可取 $p_{max}=5,q_{max}=1$
2. 取 $p\in (0,1,\cdots ,p_{m}ax),q\in (0,1,\cdots ,q_{m}ax)$，与 d 组合。d 根据 ADF 检验得来，如上例 G->L 路径可取 d = 0，构建 ARIMA 模型，同时按照 7：3 的比例将数据集切分为训练集和测试集
3. 将模型在训练集中训练并计算 AIC 指标（AIC 只能在训练的过程中计算）
4. 重复 2 -3 步骤，指导遍历完所有 p、d、q 组合，输出 AIC 最小（即最佳）的 ARIMA 模型作为预测模型。并采用 MAPE，即平均绝对偏差的百分数，在测试集中评价模型
5. 采用该预测模型预测数据的效果。

第二问求解

就以题目中的 M->U 为例吧，绘制图像

从自相关图和偏相关图可以取 $p_{max}=3,q_{max}=4$，根据 ADF 的结果：

差分0次后时序稳定
ADF检验的 p值为： 2.63e-08
检验统计量 ADF 为： -6.35

取 d = 0， $p_{max}=5,q_{max}=5$（考虑多种可能性）。根据网格寻优筛选出最佳模型为 p=1, d=0, q=3。

绘制出残差的 Q-Q 图，以观察残差是否服从正态分布：

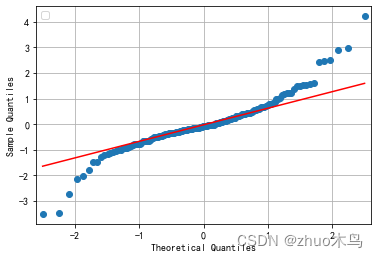
感觉还行，然后用 MAPE 数值分析他的拟合优度：
M A P E = 100 n ∑ i = 1 n ∣ y i − y i ^ ∣ y i MAPE = \frac{100}{n} \sum_{i=1}^{n} \frac{