一 概述
简单来说,混沌科学中,同一个动力学方程或者是方程组,给出的初始值相差甚微,长时间后,系统的运动轨迹却有很大差别;混沌系统广泛应用在加密等领域。
二 Matlab仿真混沌系统
以chen混沌系统为例:
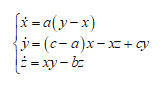
式中x,y,z
是系统的状态变量,a,b,c为该系统的常数,当参数a=35,b=3,c=28时,系统处于混沌状态。用
MATLAB
仿真得到
得到
Chen
混沌吸引子在
x-y
相面、
x-z
相面、
y-z
相面以及
x-y-z
相空间中的相轨图,如图所示

定义equation.m文件定义chen混沌方程函数
function dy=total(t,y)
%%chen circuit
a=35;b=3;c=28;
dy=[a*(y(2)-y(1));
(c-a)*y(1)-y(1)*y(3)+c*y(2);
y(1)*y(2)-b*y(3)];
end
调用实现(matlab中一般使用ODE45函数求解微分方程):
x0=[-1;-0.2;0.5];
tspan=[0:0.001:80];
[T,X]=ode45('equation',tspan,x0);
figure(1);
subplot(3,1,1),plot(T,X(:,1),'r');
xlabel('t');
ylabel('x');
subplot(3,1,2),plot(T,X(:,2),'r');
xlabel('t');
ylabel('y');
subplot(3,1,3),plot(T,X(:,3),'r');
xlabel('t');
ylabel('z');
figure(2);
plot(X(30000:end,1),X(30000:end,2));%grid;
xlabel(' x');
ylabel(' y');
figure(3);
plot(X(30000:end,1),X(30000:end,3));%grid;
xlabel(' x');
ylabel(' z');
figure(4);
plot(X(30000:end,2),X(30000:end,3));%grid;
xlabel(' y');
ylabel(' z');
figure(5);
plot3(X(30000:end,1),X(30000:end,2),X(30000:end,3));%grid;
xlabel(' y');
ylabel(' z');%%%%%%%%%%%%%%%%%%%%%%





















 1739
1739











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








