动手学深度学习笔记3.1+3.2+3.3

超大青花鱼

已于 2022-06-02 21:11:57 修改

阅读量584

点赞数 2

分类专栏：动手学深度学习文章标签：深度学习人工智能

于 2022-06-01 14:49:55 首次发布

本文链接：https://blog.csdn.net/weixin_42193791/article/details/125062843

版权

动手学深度学习专栏收录该内容

2 篇文章 1 订阅

订阅专栏

前言

前几天回想起以前做的一些小的机器学习项目（比如垃圾分类，对话模型等等），感觉自己只是按部就班的按照手册搭建模型，并没有去理解模型到底是怎么运行的，为什么模型可以运行得到这个结果，以前高中在某场中科院的巡回科普团讲座（似乎是这个名称吧，时间有点久远了）上，高中生的我回答完一个来我们学校科普的老教授在科普讲座中提出的问题后，我记得很清楚的老教授说的一句话：“遇到新事物一定要去追问为什么，而不是得过且过。”然而，在大学过程中，我走了一个大弯路，被利欲蒙蔽了身心，一味追求项目推进速度快，而忘记了去追问“为什么”，大学毕业后的我开始逐渐绕回来，试图去弥补大学期间忘记追问的为什么（当然这也一定程度上让我在考研路上付出了极大的时间成本）。
而最有意思的事情就发生在考研之后，考研过程中，我觉得高数好无聊啊，线代好无聊啊，概率论好无聊啊，整天就是背公式算数（当然在过程中我还好歹按照课程内容去推导了一些定理是怎么得来的），但是当时的数学给我的感觉就是算数，和实际生活并没有太大联系（当然纯属可能是我大学刚毕业那一年在做C#开发，已经偏离了我大学做的视觉slam和数据挖掘方向），后来为了准备面试，开始恶补计算机经典论文，可是我读论文底子非常差（因为在大学基本都是去做项目了，学术底子差的一批），于是跑了b站上去找计算机论文带读，偶然间发现了李沐博士的计算机论文带读视频，后来顺藤摸瓜找到了动手学深度学习的课程，于是乎我就买了动手学深度学习这本书，并开始一点一点画书（让我回想起当时高中把整本书画了红线），这个过程对我来说极为痛苦（因为我数学底子很差），但是越读还是越能了解高数好重要，线代好重要，概率论好重要，啊什么都好重要，于是就开了这一个系列去专门记录一下读书心得（小学初中特别讨厌读书笔记，因为要手写的手疼，还影响我专心看书，因为要顿卡一下写笔记）。
当然我特别特别特别菜，几乎没有什么数学底子和写模型的底子（），所以这一系列文章难免有很多很多错误，还请大佬们多多见谅，而且我文笔可能十分的不好，或者我完全曲解了作者在书中的意思，在这里先提前说一声对不起，当然也会出现各种啊可能雷同的情况，如果有侵犯您的权力，请联系我删除文章。

另外放一句话在这里警醒我自己：
纸上得来终觉浅，绝知此事要躬行。

绝不要因为学理论而不实践，绝不要因为去实践而不学理论。~~（这里我就不摆马圣的话了，我没资格“摆”（双层含义））~~

撒，开篇吧！

一、线性回归

1.1 线性回归概念

首先，3.1开篇就说了一句：

线性回归的输出是一个连续值，因此适用于回归问题。
分类问题中的模型的最终输出是一个离散值，softmax回归适用于分类问题。

这里我根据百度资料先来简要说一下我对线性回归的理解。
回归分析，是通过数据来确定两个或多个变量的关系。比如给你一组数据[(x=1,y=1),(x=2,y=2)]，让你确定x，y之间的关系。
根据因变量和自变量之间的关系，回归分析可以分为线性回归和非线性回归。线性回归就是指自变量和因变量之间的关系是线性的（比如y=x）。因此线性回归求解是得到一个y=f(x)的函数，并且根据y=f(x)可以计算任何的在定义域之内的自变量对应的因变量的值（说简单点，就是可以直接用x算y），因此y的值是连续的（不会出现“房价不可能10000元/平”这个事件）。

分类问题的输出是离散的（啊这个我就比较稍微熟悉一点点了，因为之前做过物体识别），分类的输出多是给出图片中物体的类别，然后再加上这个类别的置信度。通常我们会把类别抽象成一个个离散的值（比如苹果是1，橘子是2），所以分类问题的输出是离散的（不会出现”1是apple，那1.1是啥？“这种情况，因为1.1可能就没有定义）。

常见的回归问题有预测房屋价格、气温、销售额等等。
常见的分类问题有图像分类、垃圾邮件识别、疾病检测等。
在这里插入图片描述

上图是yolo v4论文中的图片。
（我之前只用过yolo v2，~~我太菜了~~，顺便感慨一下时间过得真快啊）

1.2 神经网络图

线性回归和softmax回归都是单层神经网络。

啊这个就顾名思义了，线性回归只有一个输入层和一个输出层，自然线性回归就是单层神经网络。别急别急，我知道会出现这么一个问题：一个输入层和一个输出层，那不是两层网络吗，怎么会变成单层神经网络了呢？
首先，我们先来了解一下神经网络图（当年我看论文看到这个图就头大），在深度学习中可以使用神经网络图直观的表现模型结构。
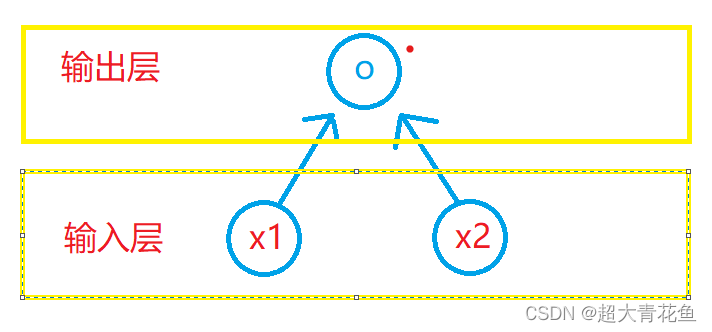
线性回归的神经网络图
如上图所示，输入层有两个输入x₁、x₂，输入个数也叫特征数或特征向量维度。输出层有一个输出o。x₁、x₂输入后，在输出层进行计算后输出o，在输出层负责计算o的单元叫神经元。由于输入层不参加计算，按照惯例，上图所示的神经网络的层数为1。
如果输出层的神经元和输入层的各个输入完全连接，输出层又可以叫做全连接层或稠密层。（各种论文中经常出现的全连接层）

线性回归的神经网络的模型类似于上图所示结构，所以线性回归的神经网络模型是单层神经网络。（当然我知道你会问这是怎么计算的啊，怎么输入之后输出就得到两个变量之间的关系了呢？这个问题先暂且搁置一下，继续向下阅读就会知道如何计算参数）

1.3 线性回归模型的基本要素

在这里，假设我们的应用要用“面积”和“房龄”预测房屋价格，接下来因变量“房屋价格”与自变量“面积”、“房龄”之间的关系。（房屋价格=f(面积，房龄)，利用线性回归找f这个运算法则）

1.3.1 模型

设房屋面积为x1，房龄为x2，售出价格为y，建立基于x1和x2的计算y的表达式，这个表达式也就是模型。
因为我们要用线性回归去分析房价，所以我们假设房价和房屋面积、房龄是线性相关的，于是得出下面这个公式。
在这里插入图片描述
上述公式中的w1、w2是权重（房价受面积、房龄影响的大小），且w1、w2均为标量（后面有些模型动不动就多维向量）。b是偏差，b为标量。
模型输出的预测值是带上划线的y（我太菜实在不知道这个上划线y咋在csdn中写）。

1.3.2 训练模型

通过数据来寻找特定的模型参数值，使模型在数据上的误差尽可能小，这个过程叫做模型训练。

收集现实生活中的数据形成一个数据集，然后在这个数据集上训练模型得到参数，并且参数得到的预测结果与实际结果误差较小。这个数据集通常被叫做训练数据集（训练集）。
比如，在预测房屋价格中，收集现实中房屋价格对应的房屋面积和房龄，形成一个数据集。这个数据集中一个访问被称为一个样本，真实价格称为标签，用来预测标签的因素（房屋面积、房龄）称为特征。

假设样本数=n（n个房屋数据），索引为i的样本（第i个房屋）的特征为x₁⁽ⁱ⁾、x₂⁽ⁱ⁾，预测值为“上划线y⁽ⁱ⁾”，房屋预测表达式为：
在这里插入图片描述

1.3.3 损失函数

在模型训练中，我们需要衡量价格预测值和真实值之间的误差。通常我们会选取一个数作为误差。

这里是重点，因为参数如何从初始值一步一步变化到最后输出的参数要依靠损失函数。我们可以使用误差来描述参数的好坏，如果误差过大（预测值和真实值相差甚远），那么说明此次参数不行，参数要变化，如果误差很小，则说明参数很接近正确的参数（参数变不变要看函数处理）。
选取一个数作为误差不是随便选的，常见的选择有平方函数（LSE，L2损失函数）、绝对值函数（LAE，L1损失函数）。在这个问题中我们使用平方函数。
别急，又出现了新名词，L1和L2是什么意思？接下来我们细说L1范数和L2范数。
首先，范数是一个数学概念，范数是一个函数，范数可以给矢量空间的所有矢量赋予非0的正长度。啊好抽象，其实你可以理解为范数是求解空间中两个点的距离的函数。
其中我们比较熟悉的欧氏距离（下式）：
在这里插入图片描述
欧式距离是范数吗？看下面这个闵可夫斯基距离公式：

闵可夫斯基距离也被称作L-P范数，其中上式中的p是变量，p = 2的时候，闵可夫斯基距离也就变为了欧式距离，即L2范数。p = 1的时候闵可夫斯基距离变为曼哈顿距离，也就是L1范数，即下述公式：
在这里插入图片描述
在机器学习里，将衡量误差的函数称为损失函数，因此使用L1范数的也就称为L1损失函数，使用L2范数的称为L2损失函数。
其实这里有一点我自己的小思考，所谓的误差，其实就是预测值到真实值之间的距离，因此我们可以使用范数来计算误差大小。L1损失函数和L2损失函数各有千秋，但L2损失函数对离群点敏感。（离群点导致的误差会平方，对参数影响较大）
说了这么多，也就是在房价预测问题中我们的损失函数选择L2损失函数，也就是评估第i个样本误差的表达式为：
在这里插入图片描述
这里出现了一个1/2，原因是方便后续对损失函数的求导（求导后函数系数变为1），在形式上会简单一些。
通常我们会用训练集中所有的样本误差的平均来衡量模型预测的质量，即下述公式：

在模型训练中，我们希望找出一组模型参数，记为w₁^*，w₂^*，b^*,来使训练样本平均损失最小。

模型训练的目的就是找出一组参数，让预测值与真实值之间的误差变得最小：
在这里插入图片描述

1.3.4 优化算法

当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来，这类解叫作解析解。
大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值，这类解叫作数值解。

数值解？解析解？这我之前听说过，学数据结构与算法中的迭代的时候，老师说过有些时候无法反解函数得到值，所以会“遍历”定义域找到解，当然我不是很喜欢迭代，因为很容易就爆栈了（~~绝不是因为我太笨了理解不了迭代~~）。当然不能乱迭代啊，不然从-∞到+∞不说模型累死，我看屏幕也要累死。所以会使用一些方法快速逼近数值解。

在求数值解的优化算法中，小批量随机梯度下降在深度学习中广泛使用。小批量梯度下降的算法很简单：
先选取一组模型参数的初始值，接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。
在每次迭代中，先随即均匀采样一个由固定数目训练数据样本组成的小批量B，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

一开始读这段话我晕了，啥啥啥咋就迭代完了？啥梯度下降？啥小批量平均误差？不着急，我们来慢慢分析这段话。
首先选模型参数的初始值，这个简单，随机选取参数嘛！但是真的简单吗？选取参数有很多中方法，比如按正态分布选取等等，这些都是后面的事情，现在我们先随机选取一组参数。
然后，随机采样组成一个小批量的数据集B，小批量数据集的大小||B||，先按照1.3.3中最后一个公式求平均损失函数：
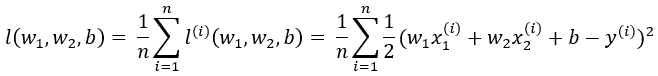
在这里插入图片描述
这个也好理解，求平均误差，减小离群点等噪音的干扰。
然后关键来了，求损失函数的梯度，这是要干啥？首先我们回忆一下高等数学，函数沿梯度下降最快。也就是说，我们沿着平均损失函数的梯度下降的话，损失会下降的最快。这样就实现了“每次迭代都可能减低损失函数的值”，而且损失函数的值降低速度最快。（这也是不随便选取迭代值的原因，降低损失函数的值有多条路径，但沿梯度这条路径下降最快）
在这里插入图片描述
（3D图画法参考https://blog.csdn.net/zhuoqingjoking97298/article/details/122283172，小声BB几句，回去引用这篇文章的时候发现是卓晴大大的文章，~~回想起被飞卡调车支配的恐惧~~）
“最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。”这句话就更好理解了，求出梯度后，我们将参数减去一个固定值*梯度，这样迭代的参数就会让损失值降低的最快。
上述提到了一个固定值，这个固定值也被称作学习率，是提前人为设定好的。同样的，小批量样本的大小也是提前人为设定的，这样人为设定的参数不是通过训练得出的，因此被称为超参数。所谓的调参正是调节超参数。少数情况下超参数也可以通过模型训练学出。
在这里插入图片描述
回忆一下高数，运用链式求导法则，设学习率为η，小批量样本的大小为|B|，得到迭代参数的计算公式：

在这里插入图片描述

1.3.5 模型预测

模型训练完成后，我们将模型参数w₁、w₂、b在优化算法停止时的值分别记作w₁^*、w₂^*、b^*，这里我们这里得到的并不一定是最小化损失函数的最优解，而是对最优解的一个近似。然后，我们就可以使用学出的线性回归模型来估算训练数据集以外任意一栋面积为x₁、房龄为x₂的房屋的价格了。这里的估算也叫做模型预测、模型推断或模型测试。

这段话没啥需要解释的了，训练完成后拿着模型快快乐乐的跑到测试集上去跑一圈（~~结果过拟合或欠拟合了~~）。

二、代码实现

2.1 从零开始实现线性回归

2.1.1 导入库

import random                        #随机数生成
import torch                         #pytorch
from d2l import torch as d2l        #d2l是动手学深度学习书中带的库

2.1.2 生成数据集

由于房价预测问题只是我们自己一个抽象问题，所以并没有真实的数据集，因此我们要自己生成一个数据集供我们训练模型。

在下面代码中，我们将生成一个包含1000个样本的数据集，每个样本包含从标准正态分布中采样的2个特征。我们的合成数据集是一个矩阵X∈R^1000*2。
我们使用线性模型参数w = [2,-3.4]^T、b = 4.2和噪声项c，生成数据集及其标签。

def synthetic_data(w,b,num_examples):
    X = torch.normal(0,1,(num_examples,len(w)))    
    #torch.normal是从正态分布提取随机张量的函数
    #torch.normal的第一个参数是均值，第二个参数是标准差，第三个参数是张量形状
    y = torch.matmul(X,w)+b                #torch.matmul是矩阵乘法，表达式为y=Xw+b
    y += torch.normal(0,0.01,y.shape)      #随机正态分布生成噪声，为y添加噪声
    return X,y.reshape((-1,1))            #reshape(-1,1)重新生成m行1列的张量，-1代表自动计算张量行数

这里比较好理解，我们从正态分布随机抽样出来两个特征（房屋面积，房龄），抽样了1000次，按照下述公式生成了1000个样本：
在这里插入图片描述
（稍微插一嘴，这一步就好像你在高中做化学实验提取盐，一般都是化学老师在精盐（真实数据）中混杂沙子（噪声）等形成粗盐，然后通过一系列复杂操作提取出氯化钠，这不是因为粗盐很难买到，而是因为粗盐溶解速度太慢，凭一根玻璃棒搅动到溶化可能~~会累死~~到下课）

true_w = torch.tensor([2,-3.4])                        #设定的真实的w1、w2为2、-3.4
true_b = 4.2                                           #真实的b为4.2
features,labels = synthetic_data(true_w,true_b,1000)   #生成样本集

print('features:',features[0],'\nlabel:',labels[0])    #打印样本集中第一个特征和标签
d2l.set_figsize()
d2l.plt.scatter(features[:,(0)].detach().numpy(),labels.detach().numpy(),1)
#画第一个特征与标签之间的关系
d2l.plt.scatter(features[:,(1)].detach().numpy(),labels.detach().numpy(),1)
#画第二个特征与标签之间的关系

生成数据集结果如下图：
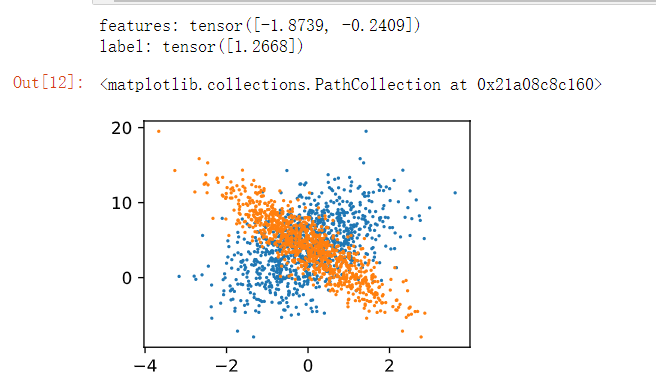
在这里插入图片描述
上图中蓝点为第一个特征，橙点为第二个特征，能看出来第一个特征大致与标签成正比，第二个特征与标签成反比。

2.1.3 读取数据集

在下面代码中，我们定义一个data_iter函数，该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。每个小批量包含一组特征和标签。

def data_iter(batch_size,features,labels):
    num_examples = len(features)                    #获得数据集大小
    indices = list(range(num_examples))             #生成一个数据集大小的数据序号（0，1，2，……，num_examples-1）列表
    random.shuffle(indices)                         #随机打乱序号列表
    for i in range(0,num_examples,batch_size):     #将列表分为若干个batch_size大小的分组，每次遍历一个分组
        batch_indices = torch.tensor(indices[i:min(i + batch_size,num_examples)])
        #取第i到i+batch_size个序号，最后一个取i到num_examples
        yield features[batch_indices],labels[batch_indices]        #返回features，labels

batch_size = 10

for X,y in data_iter(batch_size,features,labels):
    print(X,'\n',y)
    break

输出如下图所示：
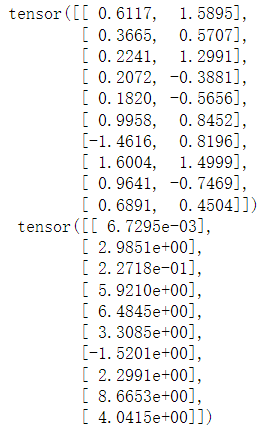
在这里插入图片描述

上面实现的迭代对于数学来说很好，但它的执行效率很低，可能会在实际问题中陷入麻烦。例如，它要求我们将所有数据加载到内存中，并执行大量的随机内存访问。在深度学习框架中实现的内置迭代器效率要高很多，它可以处理存储在文件中的数据和数据流提供的数据。

2.1.4 初始化模型参数

在下面的代码中，我们通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重，并将偏置初始化为0.

w = torch.normal(0,0.01,size=(2,1),requires_grad = True)
b = torch.zeros(1,requires_grad = True)
#requires_grad是Pytorch中通用数据结构Tensor的一个属性，用于说明当前量是否需要在计算中保留对应的梯度信息

啊开始抽象一点了，啥权重，啥偏置？其实权重就是模型“y=w₁x₁+w₂x₂+b”中的w₁、w₂，偏置就是b。

2.1.5 定义模型

接下来，我们必须定义模型，将模型的输入和参数同模型的输出关联起来。回想一下，要计算线性模型的输出，我们只需计算输入特征X和模型权重w的矩阵-向量乘法后加上偏置b。注意，上面的Xw是一个向量（张量），而b是一个标量。回想一下2.1.3节中描述的广播机制，当我们用一个向量加一个标量时，标量会被加到向量的每个分量上。

def linreg(X,w,b):
    return torch.matmul(X,w)+b

这里提到了一个广播机制，广播机制在书中的2.1.3节中的描述如下：

在某些情况下，即使形状不同，我们仍然可以通过调⽤⼴播机制（broadcasting mechanism）来执⾏按元素操作。这种机制的⼯作⽅式如下：⾸先，通过适当复制元素来扩展⼀个或两个数组，以便在转换之后，两个张量具有相同的形状。其次，对⽣成的数组执⾏按元素操作。

也就是说，当两个数组进行某种操作时，如果两个数组之间的形状不满足操作要求，那么就会对一个数组进行复制元素的操作来扩展数组，达到操作要求。比如[1,2,3]^T与1相加，就会变成[1,2,3]^T+[1,1,1]^T
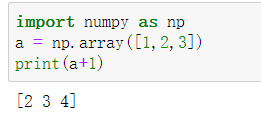
在这里插入图片描述
广播机制可以方便我们操作张量，但是使用不当也会导致程序崩溃，所以在使用广播机制的时候要谨慎。

2.1.6 定义损失函数

因为需要计算损失函数的梯度，所以我们应该先定义损失函数。这里我们使用平方损失函数。在实现中，我们需要将其真实值y的形状转换为和预测值y_hat的形状相同。

def squared_loss(y_hat,y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

这里容易理解，如果y和y_hat形状不同，运算出的结果也是错误的。

2.1.7 定义优化算法

在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。接下来，朝着减少损失的方向更新我们的参数。下面的函数实现小批量随机梯度下降更新。该函数接受模型参数集合、学习速率和批量大小作为输入。每一步更新的大小由学习速率lr决定。因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size）来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。

def sgd(params,lr,batch_size):
    with torch.no_grad():
        #即使一个tensor的requires_grad = True，在with torch.no_grad计算，得到的新tensor的requires_grad也为False，即不会对新tensor求导
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

这里有一个with torch.no_grad，参考下属文章：
https://blog.csdn.net/sazass/article/details/116668755
这里还提到了用批量大小来规范步长，我的理解是，每一步的更新要受学习率和批量大小两个的影响。

2.1.8 训练模型

在每次迭代中，我们读取一小批量训练样本，并通过我们的模型获得一组预测。计算完损失后，我们开始反向传播，存储每个参数的梯度。最后我们调用优化算法sgd来更新模型参数。
概括一下，我们将执行一下循环：
1.初始化参数
2.重复以下训练，直到完成：
（1）计算梯度，公式参照下面第一个图
（2）更新参数，(w,b) ←(w,b) - ηg
在每个迭代周期（epoch）中，我们使用data_iter函数遍历整个数据集，并将训练数据集中所有的样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03.设置超参数很棘手，需要通过反复试验进行调整。

for epoch in range(num_epochs):
    for X,y in data_iter(batch_size,features,labels):
        l = loss(net(X,w,b),y)            #求损失
        l.sum().backward()                #反向传播求梯度，这里l时一个（batch_size,1）形状的张量，所以加在一起求导
        sgd([w,b],lr,batch_size)          #使用优化算法迭代参数
    with torch.no_grad():
        train_l = loss(net(features,w,b),labels)
        print(f'epoch{epoch + 1},loss {float(train_l.mean()):f}')

在这里插入图片描述

这里提到了反向传播，反向传播又是什么呢？
在这里你可以将反向传播理解为求偏导然后存储起来即可，更为详细的定义在后面添加隐藏层后描述。

2.1.9 结果

辛辛苦苦捣腾完这些代码块，看看模型训练得到的参数和我们设置的真实参数相差多少吧！

print(f'w的估计误差：{true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差：{true_b - b}')

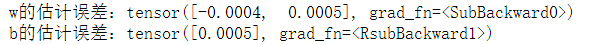
在这里插入图片描述

2.2 线性回归简化实现

~~挖个坑，今天有点累了，后续再填。~~
——————————————————————————————————————————
6月2日前来填坑。

2.2.1 生成数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w =torch.tensor([2,-3.4])
true_b = 4.2
features,labels = d2l.synthetic_data(true_w,true_b,1000)

其中的synthetic_data在之前从零开始实现线性回归中已经实现过这个函数了。

2.2.2 读取数据集

我们可以调用框架中现有的API来读取数据。我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。

def load_array(data_arrays,batch_size,is_train = True):
    dataset = data.TensorDataset(*data_arrays)                        #封装标签和特征值（其实就是将标签与对应的特征值生成一个数据集tensor）
    return data.DataLoader(dataset,batch_size,shuffle=is_train)       #切分数据集，每次取batch_size大小的数据，每次打乱数据

batch_size = 10
data_iter = load_array((features,labels),batch_size)

TensorDataset函数和DataLoader函数详情可以参考这几篇文章：
https://blog.csdn.net/qq_38406029/article/details/121282487
https://blog.csdn.net/qq_39507748/article/details/105385709?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7ECTRLIST%7EPayColumn-1-105385709-blog-121282487.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7ECTRLIST%7EPayColumn-1-105385709-blog-121282487.nonecase&utm_relevant_index=1
https://blog.csdn.net/weixin_40539952/article/details/116463705?utm_medium=distribute.pc_relevant.none-task-blog-2_defaultbaidujs_baidulandingword~default-3-116463705-blog-105385709&spm=1001.2101.3001.4242.2&utm_relevant_index=6

在这个load_array函数中简单来说，TensorDataset函数就是封装标签和特征值形成一个数据集，DataLoader函数就是从指定数据集取数据。

使用data_iter的方式与之前从零实现线性回归中使用data_iter的方式相同。为了验证是否正常工作，让我们读取并打印第一个小批量样本。与上述不同，这里我们使用iter构造Python迭代器，并使用next从迭代器中获取第一项。

next(iter(data_iter))

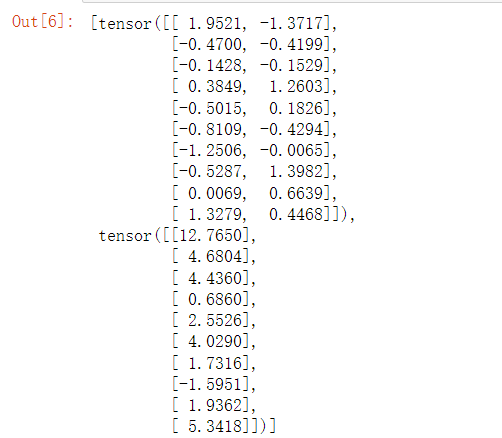
在这里插入图片描述

Python中内带的函数iter()的功能是：生成一个迭代器，也就是不断迭代数据。
举例子就是：a = [1，2，3]，iter(a)之后生成一个迭代器a_iter，a_iter可以不断的按顺序从a中取出值（也就是a_iter在不停的迭代数据）。
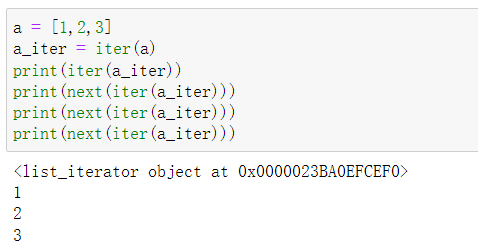
在这里插入图片描述
iter函数还有更好玩的用法，可以参考下面这篇文章：
https://blog.csdn.net/max_LLL/article/details/124243287

2.2.3 定义模型

在Pytorch中，全连接层在Linear类中定义。值得注意的是，我们将两个参数传递到nn.Linear中。第一个指定输入特征形状，即2，第二个指定输出特征形状，输出特征形状为单个标量，因此为1.

from torch import nn

net = nn.Sequential(nn.Linear(2,1))

nn.Sequential()可以将括号内的模块或模型依次串到一起形成一个网络，也就是说，nn.Sequential()可以帮助我们快速搭建网络，nn.Sequential()这个函数在后面会经常使用。不过在上述代码中只是添加了一个输入特征形状为2、输出特征形状为1的全连接层。（回忆一下，输入特征是房屋面积和房龄，也就是输入特征形状为2，输出为预测的房价，是一个标量，也就是输出特征为1。）
全连接层的构建nn.Linear()可以参考这篇文章：
https://blog.csdn.net/qq_42079689/article/details/102873766

2.2.4 初始化模型参数

在这里，我们指定每个权重参数应该从均值为0，标准差为0.01的正态分布中随机采样，偏执参数将初始化为零。
正如我们在构造nn.Linear时指定输入和输出尺寸一样，现在我们能直接访问参数以设定它们的初始值。我们可以通过net[0]选择网络中的第一个图层，然后使用weight.data和bias.data方法访问参数。我们还可以使用替换方法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0,0.01)       #normal_(a,b)就是用均值为a，标准差为b的正态分布填充
net[0].bias.data.fill_(0)                #fill_(a)就是用a填充

2.2.5 定义损失函数

计算均方误差使用的是MSELoss类，也称为平方L2范数。默认情况下，它返回所有样本损失的平均值。

loss = nn.MSELoss()         #MSELoss()就是均方误差函数，也称为平方L2范数

在这篇文章的前半部分介绍了均方误差函数也叫LSE，也就是L2损失函数。

2.2.6 定义优化算法

小批量随机梯度下降算法是一种优化神经网络的标准工具，PyTorch在optim模块中实现了该算法的许多变种。当我们实例化一个SGD实例时，我们要指定优化的参数（可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。小批量随机梯度下降只需要设置lr值，这里设置为0.03。

trainer = torch.optim.SGD(net.parameters(),lr=0.03)    
#torch.optim.SGD()是梯度下降函数，第一个参数是待优化的参数，第二个参数是学习率
#net.parameters()返回了net里面的参数

2.2.7 训练

在每个迭代周期里，我们将完整遍历一次数据集（tarin_data），不停地从中获取一个小批量的输入和相应的标签。对于每一个小批量，我们会进行以下步骤：
·通过调用net(X)生成预测并计算损失l（前向传播）。
·通过进行反向传播来计算梯度。
·通过调用优化器来更新模型参数。

~~（敲了不下二十遍我终于一遍把引用完全敲对了ohhhhhhhhhhh）~~

num_epochs = 3
for epoch in range(num_epochs):
    for X,y in data_iter:
        l = loss(net(X),y)             #计算训练样本的预测值和真实值之间的误差
        trainer.zero_grad()            #将梯度置为零
        l.backward()                   #反向传播求梯度
        trainer.step()                 #梯度下降优化参数
    l = loss(net(features),labels)     #计算此时优化后的参数预测的数值和真实数值之间的误差
    print(f'epoch {epoch + 1},loss {l:f}')

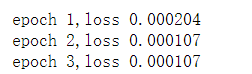
在这里插入图片描述

下面我们比较生成数据集的真实参数和通过有限数据训练获得的模型参数。要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置。

w = net[0].weight.data
print('w的估计误差：',true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：',true_b - b)

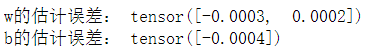
在这里插入图片描述

这里的bias就是偏置，也就是上述模型中的“b”。

总结

回到最开始的地方，我发现仅仅就是一个简单的线性回归问题，就用到了高数中的链式求导和梯度，线代中的向量（张量），更别说后面的softmax里面的交叉熵损失函数里面还要使用概率论的最大似然估计（一种推导角度，交叉熵和最大似然估计有异曲同工之处）。可以看出，机器学习对数学底子还是有一定要求的，像我这样的彩笔就边学边补数学知识，这篇博客整整写了八个小时，写的的确有点慢了，因为要不断查资料来确定一些地方，图片也要一点点截，下面贴上引用的文章和动手学深度学习这本书的官方网址：
动手学深度学习：https://zh-v2.d2l.ai/
李沐博士的课程：https://www.bilibili.com/video/BV1if4y147hS?spm_id_from=333.880.my_history.page.click
with no_grad：https://blog.csdn.net/sazass/article/details/116668755
线性回归：https://blog.csdn.net/qq_36330643/article/details/77649896
范数：https://zhuanlan.zhihu.com/p/137073968
Python画3D图：https://blog.csdn.net/zhuoqingjoking97298/article/details/122283172
化学实验提取粗盐：https://www.bilibili.com/video/BV1zf4y1776m?spm_id_from=333.880.my_history.page.click
yolov4：
https://arxiv.org/pdf/2004.10934.pdf
https://blog.csdn.net/hgnuxc_1993/article/details/120724812

超大青花鱼

关注

2
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
动手学深度学习笔记3.1+3.2+3.3

文章目录前言一、线性回归1.1 线性回归概念1.2 神经网络图1.3 线性回归模型的基本要素1.3.1 模型二、代码实现1.引入库2.读入数据总结前言前几天回想起以前做的一些小的机器学习项目（比如垃圾分类，对话模型等等），感觉自己只是按部就班的按照手册搭建模型，并没有去理解模型到底是怎么运行的，为什么模型可以运行得到这个结果，以前高中在某场中科院的巡回科普团讲座（似乎是这个名称吧，时间有点久远了）上，高中生的我回答完一个来我们学校科普的老教授在科普讲座中提出的问题后，我记得很清楚的老教授说的一句话：“
复制链接

扫一扫