蒙特卡洛法计算圆周率π（Python，Java，c 三种方式详解）

一、蒙特卡洛法简介

蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

---

二、蒙特卡洛法计算圆周率的原理

正方形的面积为：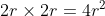

圆的面积为：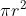

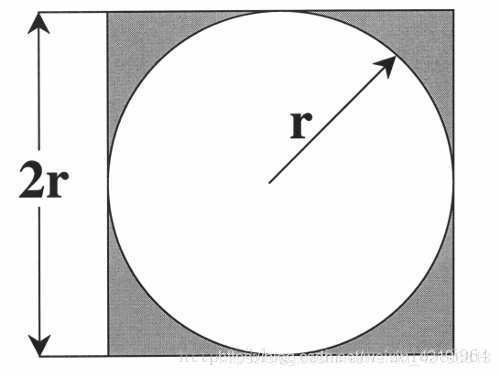
圆的面积比上正方形的面积为：π / 4

所以我们使用蒙特卡洛法在正方形内随机撒点，落在圆内的点 / 落在正方形内的点（全部的点），就约等于圆的面积 / 正方形的面积 = π / 4

三、使用编程语言实现计算过程

1、Python实现蒙特卡洛法计算圆周率π

import random

def count_pi(n):
    i = 0
    count = 0
    # n 为传入的总点数量
    while i < n:
        # 随机产生x,y坐标
        x = random.random()
        y = random.random()
        # 如果x平方 + y平方 < 1，说明在圆内
        if (pow(x, 2) + pow(y, 2)) < 1:
            count += 1
        i += 1
    # π的值为：4 * （落在圆内的点/总的点）
    return 4 * (count / n)


pi = count_pi(100000)
print(pi)

2、Java实现蒙特卡洛法计算圆周率π

package practice;

/**
 * 
 * @author 你的坏机器人
 * @邮箱：2602341707@qq.com
 * @修改日期：2020.1.30
 * @描述：使用蒙特卡洛方法计算圆周率π的值
 *
 */
public class MonteCarlo {

	public double countPI(double n) {
		int i = 0;
		int count = 0;
		double pi = 0;
		double x = 0;
		double y = 0;
		while(i < n) {
			x = Math.random();
			y = Math.random();
			if ((x * x) + (y * y) < 1) {
				count++;
			}
			i++;
		}
		pi = 4 * (count / n);
		return pi;
	}
	
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		MonteCarlo monteCarlo = new MonteCarlo();
		double pi = 0;
		pi = monteCarlo.countPI(100000);
		System.out.println("蒙特卡洛计算圆周率pi的值为："+pi);
	}

}

3、c语言实现蒙特卡洛法计算圆周率π

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

double countPI(double n)
{
	int i = 0;
	int count = 0;
	double pi = 0;
	double x = 0;
	double y = 0;
	srand((unsigned)time(NULL));
	while (i < n)
	{
		x = rand() / (double)(RAND_MAX);
		y = rand() / (double)(RAND_MAX);
		if ((x * x) + (y * y) < 1)
		{
			count++;
		}
		i++;
	}
	pi = 4 * (count / n);
	return pi;
}

int main(){
	double pi = 0;
	pi = countPI(100000);
	printf("%lf\n",pi);
	return 0;
}

早在17世纪，人们就知道用事件发生的“频率”来决定事件的“概率”。这也是蒙特卡洛法的基本思想。当样本数量足够大时，我们可以用频率去估计概率。这也是求圆周率π的常用方法。