BFGS算法及其matlab实现

 

目录

 一.前沿

二.基本思想

三.秩2校正公式

 四.算法步骤

 五.matlab程序实现

---

 一.前沿

上一篇文章介绍了基于秩1的拟牛顿算法，紧接上文，这次我们介绍关于秩2的拟牛顿算法，即BFGS算法。为啥叫BFGS算法，是因为这个鬼算法是由Broyden、Fletcher、Goldforb和Shanno这四个大佬发明的，BFGS校正算法是目前最流行，也是最有效的拟牛顿校正。

二.基本思想

拟牛顿法的基本思想是把牛顿法中用到的Hess阵用一个Hk矩阵来代替。那么Hk是什么呢？Hk的三个特点如下：

（1）Hk近似等于牛顿法中的Hess阵，这样可以保证拟牛顿发所产生的方向与牛顿反向近似，从而保证了拟牛顿法的收敛速度。

（2）Hk是正定的

（3）Hk的更新规则有两种，即用秩1或秩2的矩阵矫正。上篇文章介绍的是秩1算法，所以这篇文章介绍秩2算法。（秩1秩2法其实就是两个更新Hk的不同公式，应该是记住就行了吧，反正推导我也看不懂）。

三.秩2校正公式

在做matlab仿真时，H0通常用一个单位矩阵来代替。经过一次迭代后，Hk的秩2矫正公式如下（手写吧，打公式太痛苦了）：

 

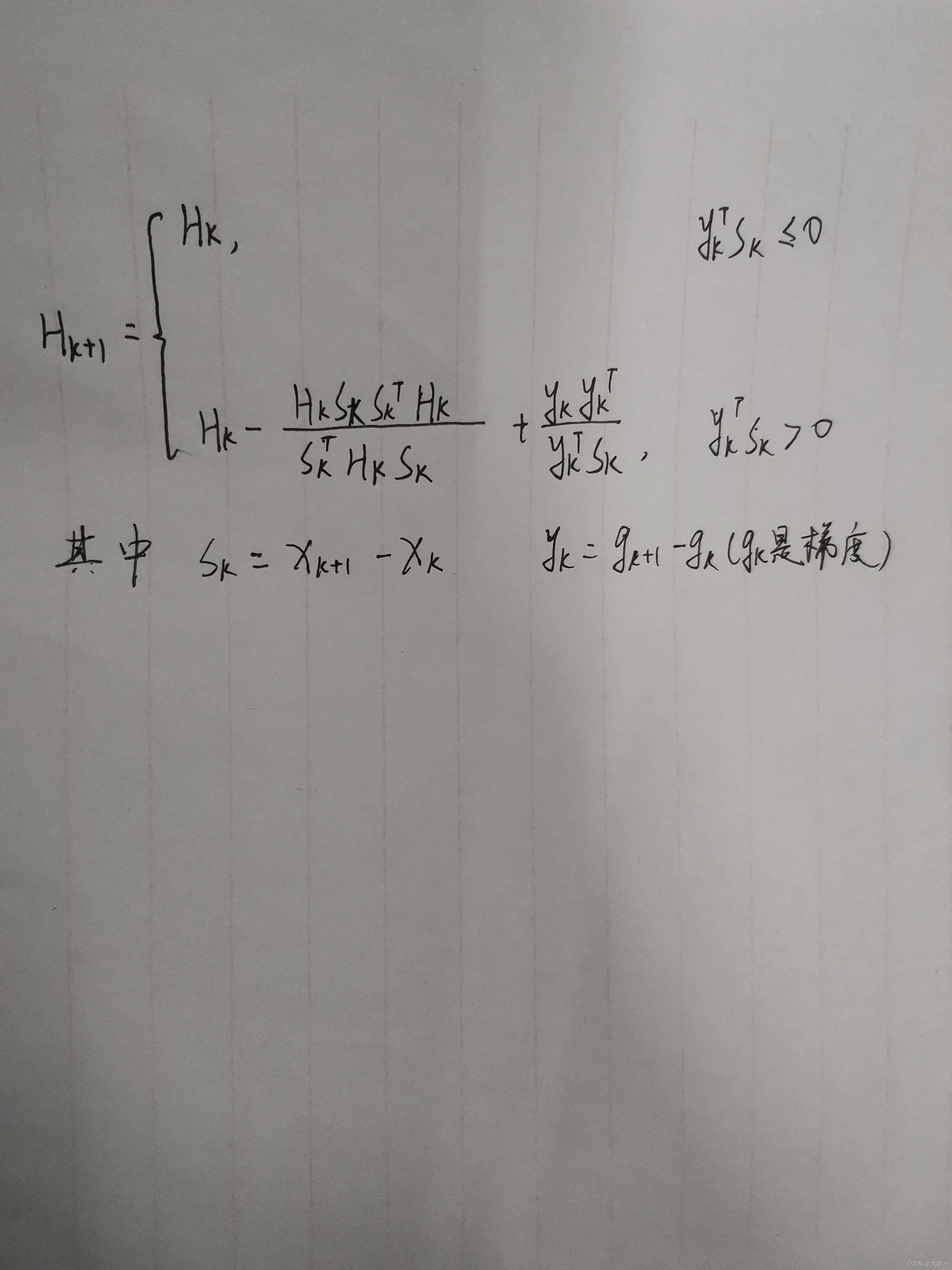
 四.算法步骤

步0：确定终止误差e=（0~1），设初始点x0，=(0~1)，=（0,0.5），初始对称正定阵H0=I（单位阵），令k=0

步1：计算gk=f(xk).若||gk||<=e,停算，输出xk作为最优解。否则，转步2

 步2：解线性方程组 Hk*dk= -gk，解出dk（即得出搜索方向）

步3：用Armjio搜索技术求步长k=^mk，m的值从0开始，

若f(xk+ ^m*dk)<=f(xk)+*^m*gk'dk 

则 mk=m，步长k=^mk，若不满足上式，则m=m+1，直到满足上述不等式为止 

步4：令Xk+1=xk+ k*dk

步5：由校正公式确定Hk+1，即上图所示。令k=k+1，转步1

 五.matlab程序实现

BFGS封装函数：

function [x,val,k]=bfgs(fun,gfun,x0,varargin)
k=0;
maxk=500;
rho=0.55;
sigma=0.4;
e=1e-5;%精度
n=length(x0);
Hk=eye(n);
while(k<maxk)
    gk=feval(gfun,x0,varargin{:});
    if(norm(gk)<e),break;end
    dk=-Hk\gk;%在后面会更新Hk
    m=0;
    mk=0;
    while(m<20)
        s=feval(fun,x0+rho^m*dk,varargin{:});
        a=feval(fun,x0)+sigma*rho^m*gk'*dk;
        if(s<a)
         mk=m;
         break;
        end
         m=m+1;
        end
        x=x0+dk*rho^mk;
        sk=x-x0;
        yk=feval(gfun,x,varargin{:})-gk;
        if(yk'*sk>0)
          Hk=Hk-(Hk*sk*sk'*Hk)/(sk'*Hk*sk)+(yk*yk')/(yk'*yk);
        end
    x0=x;
    k=k+1;
end
val=feval(fun,x0,varargin{:});
end

其中fun,gfun，main函数在上篇文章都有。