CG
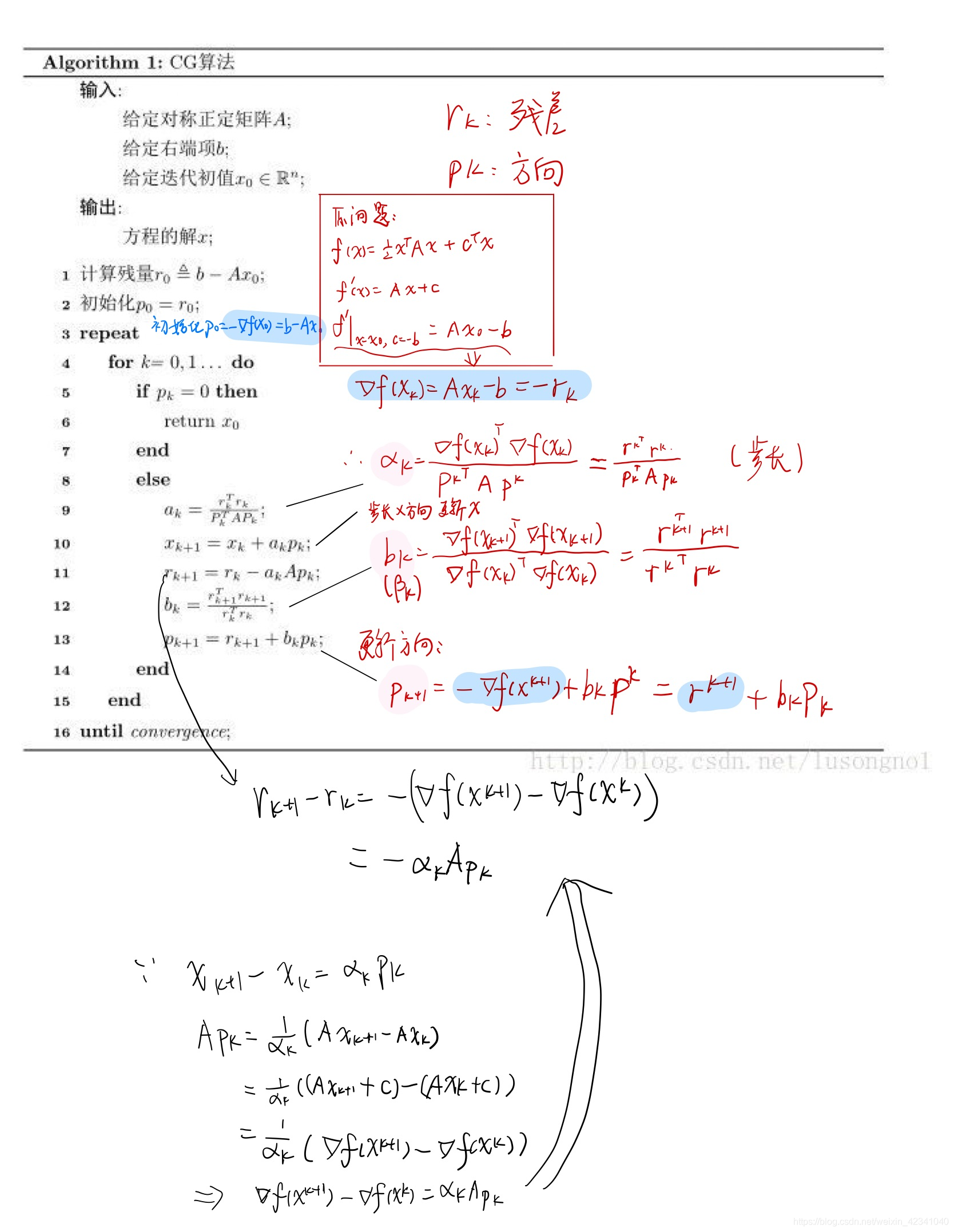
C实现
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
#define N 5
#define epsilon 0.005
void matrixTimesVec(double A[N][N], double b[N], double Ab[N])
{
int i, j;
for (i = 0; i < N; i++)
{
Ab[i] = 0.0;
for (j = 0; j < N; j++)
{
Ab[i] = Ab[i] + A[i][j] * b[j];
}
}
}
double scalarProduct(double vec1[], double vec2[])
{
double s = 0;
int i;
for (i = 0; i < N; i++)
{
s = s + vec1[i] * vec2[i];
}
return s;
}
void vecPlus(double vec1[], double vec2[], double vec[])
{
int i;
for (i = 0; i < N; i++)
{
vec[i] = vec1[i] + vec2[i];
}
}
void numPlusVec(double num, double vec0[], double vec[])
{
int i;
for (i = 0; i < N; i++)
vec[i] = num * vec0[i];
}
int main()
{
int i, j;
static double A[N][N] = { 1,1,1,1,1,
1,2,2,2,2,
1,2,3,3,3,
1,2,3,4,4,
1,2,3,4,5 };
static double b[N] = { 1, 25, 31, -4, 5 };
static double x0[N] = { 1.4, -9, 23, 4, 1.9 };
double x[N], r[N], p[N], w[N], alpha, rho00, rho0, rho1, beta;
printf("\n要求解的示例方程组为:\n A ||| b \n");
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
printf("%f ", A[i][j]);
}
printf("||| %f\n", b[i]);
}
printf("初始解x0为:\n");
for (int i = 0; i < N; i++) {
printf("%f ",x0[i]);
}
memcpy(x, x0, N * sizeof(double));
double Ax0[N];
matrixTimesVec(A, x0, Ax0);
numPlusVec(-1.0, Ax0, Ax0);
vecPlus(b, Ax0, r);
rho0 = scalarProduct(r, r);
rho00 = rho0;
memcpy(p, r, N * sizeof(double));
int iter = 0;
do
{
matrixTimesVec(A, p, w);
alpha = rho0 / (scalarProduct(p, w));
double temp[N];
numPlusVec(alpha, p, temp);
double x_temp[N];
vecPlus(x, temp, x_temp);
memcpy(x, x_temp, N * sizeof(double));
numPlusVec(-alpha, w, temp);
double r_temp[N];
vecPlus(r, temp, r_temp);
memcpy(r, r_temp, N * sizeof(double));
rho1 = scalarProduct(r, r);
beta = rho1 / rho0;
numPlusVec(beta, p, temp);
vecPlus(r, temp, p);
rho0 = rho1;
iter++;
} while (rho1 > epsilon);
printf("\n\n");
printf("方程组的解为:\n");
for (i = 0; i < N; i++)
printf("%f\n", x[i]);
printf("迭代了%d次", iter);
return 0;
}
结果
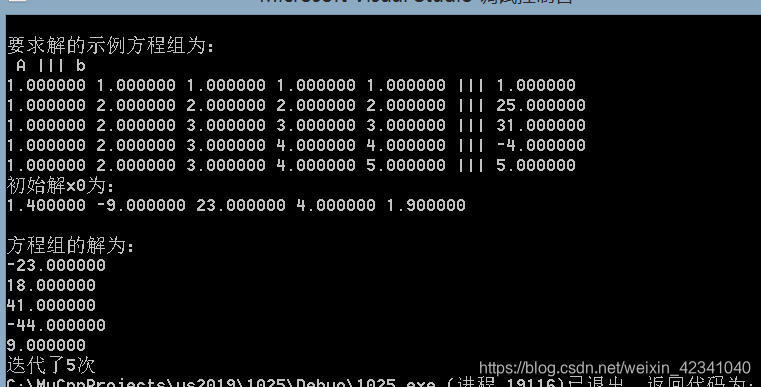


























 1031
1031

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








