基于DFM模型的学生消费行为分析

基于DFM模型的学生消费行为分析

[摘要]本文主要通过对已有的国内某高校校园一卡通系统一个月的运行数据进行研究，最终建立了具有较高实用性的学生消费行为分析模型。

针对问题一

我们在对已知的数据进行预处理的基础上，对表二的消费记录进行深入的分析，我们的研究方向主要有三个：早午晚各食堂就餐人次占比的可视化，分析每个食堂的三餐就餐情况；工作日与休息日就餐人数与时间的关系的可视化，分析每个时段食堂的就餐高峰期，还有工作日和休息日的高峰期有什么不同；食堂餐费和食堂就餐人数的关系，从统计的角度出发，通过Pearson线性相关系数来评判两者之间的联系，得出了食堂餐费和食堂就餐人数之间存在比较紧密的负相关现象。

第一食堂三餐需要大幅改进，可以考虑降低价格、增加菜式、改善食堂就餐环境等措施；第二和第五食堂在三餐中都比较受欢迎，可以考虑增开窗口来缓解目前就餐压力；第三、第四食堂的早餐比较冷门，建议只开一个窗口或直接取消；工作日的9:40和16:20存在就餐高峰，食堂要提前做好准备；休息日食堂注意减少供应，以免造成浪费，休息日的早餐持续时间较长，食堂要注意进行保温和分批供应。

针对问题二

通过对学生的消费记录的进一步探究，提出了DFM模型，主要建立在月平均余额、消费频率和月总消费额三个指标上。通过Elbow Method法对K-Means算法的最佳K值进行了分析，然后采用了优化过后的K-Means++方法，对学生进行聚类，在此过程中发现了存在部分异常数据，比如一个月消费次数个位数的人群，经过了进一步清洗后再此聚类，发现结果有了比较大的提升。最终，分析了每个类型学生的消费特点。

通过聚类绘制三维散点图，将学生消费人群大致分成了6类，对低中高等的消费人群进行了初步的分类，简要推测了不同消费行为对应的消费人群。我们定义的DFM模型能初步根据消费特点对学生群体进行分类。

针对问题三

在问题二的模型基础上，我们选择了其中的需要补助的可能性最大的一类人进行了基于AHP的打分，最终得到的区间为1-5分，分数越低说明消费水平比较低，最后根据分数划分群体后，提出梯度补助的策略。

对分值1的人群为重点补助人群，分值2和3的人群为基本补助人群，分值为4的人群可以少量补助，分值为5的人群极有可能是上一个模型的漏网之鱼，不补助。综上可知，我们建立的结合AHP分析的DFM模型具有较高的实际价值。

关键字:DFM模型 K-Means++聚类 层次分析法

• 问题重述

1.1问题的背景

校园一卡通是集身份认证、金融消费、数据共享等多项功能于一体的信息集成系统。在为师生提供优质、高效信息化服务的同时，系统自身也积累了大量的历史记录，其中蕴含着学生的消费行为以及学校食堂等各部门的运行状况等信息。很多高校基于校园一卡通系统进行“智慧校园”的相关建设，例如《扬子晚报》2016年1月27日的报道：《南理工给贫困生“暖心饭卡补助”》。  不用申请，不用审核，饭卡上竟然能悄悄多出几百元……记者昨天从南京理工大学独家了解到，南理工教育基金会正式启动了“暖心饭卡”项目，针对特困生的温饱问题进行“精准援助”。 项目专门针对贫困本科生的“温饱问题”进行援助。在学校一卡通中心，教育基金会的工作人员找来了全校一万六千余名在校本科生9月中旬到11月中旬的刷卡记录，对所有的记录进行了大数据分析。最终圈定了500余名“准援助对象”。 南理工教育基金会将拿出“种子基金”100万元作为启动资金，根据每位贫困学生的不同情况确定具体的补助金额，然后将这些钱“悄无声息”的打入学生的饭卡中，保证困难学生能够吃饱饭。

——《扬子晚报》2016年1月27日：南理工给贫困生“暖心饭卡补助”

1.2问题的相关信息

附件包含3张数据表，分别为data1.csv、data2.csv、data3.csv。可知如下数据：

表1为学生ID表，给出4341条记录，包含字段为序号、校园卡号、性别、专业名称和门禁卡号。

表2为消费记录表，给出519367条记录，包含字段为流水号、校园卡号、校园卡编号、消费时间、消费金额、存储金额、余额、消费次数、消费类型、消费项目的编码、消费项目的序列号、消费操作的编号、操作编码和消费地点。

表3为门禁记录表，给出43156条记录，包含字段为序号、门禁卡号、进出时间、进出地点、是否通过和描述。

1.3需解决的问题

本赛题提供国内某高校校园一卡通系统一个月的运行数据，请使用附件数据分析和建模，分析学生在校园内的学习生活行为，为改进学校服务并为相关部门的决策提供信息支持。  

问题一：分析学生的消费行为和食堂的运营状况，为食堂运营提供建议。  

问题二：根据学生的整体校园消费行为，选择合适的特征，构建模型，分析每一类学生群体的消费特点。  

问题三：构建学生消费细分模型，为学校判定学生的经济状况提供参考意见。

• 
  模型假设

（1）假设附件中所给的学生信息和消费记录数据都是真实可靠的；

（2）假设所有记录的消费是合理的，不存在恶意消费；

（3）假设一条消费记录代表一次消费，即不存在同一次消费产生多条记录的情况。

（4）假设一个月消费次数少于30次的都是不正常的消费现象。

（5）假设在月平均余额、消费频率和月总消费额三个指标中月总消费额对于评价学生的经济能力最重要，其次是消费频率，最后才是月平均余额。

（其余假设在文中另作说明）

• 符号说明

（其余符号在文中另作说明）

• 数据预处理

4.1处理数据类型

因为原Date字段是以<年/月/日 时:分>的形式给出的，我们为了统计不同天和不同时段的数据，所以将data2.csv中Date字段拆分为时间Time和日期Data两个字段。

4.2 处理重复数据

删除data2.csv中的重复数据项。考虑CardNo和CardCount，如果一张卡消费过，但是消费次数是一样的，说明记录是重复的，需要删除。

4.3 处理异常值和空值

data2.csv中，探索TermSerNo字段，发现基本为空值，但是有小部分数据是非空值的，其对应的时间却都在零点，因此判断此为异常数据，删除此字段不为空的数据；探索conOperNo字段，发现也有小部分的非空数据，其对应的类型为非消费类型，主题为消费，因此删除此字段不为空的数据。

4.4 筛选消费数据

data2.csv中，虽然在去空值的时候，有对一部分非消费类型进行处理，但是还有部分非消费类型没有被去除，筛选Type字段为“消费”的记录。

4.5 删除多余字段

data2.csv中，TermSerNo、conOperNo、FundMoney和Type这几个字段在以上处理中，清洗了部分数据，剩下的内容对后续分析没有作用，因此对这几个字段进行删除。Index和PeoNo字段因为是编号，没有实际的作用，这里也对其进行删除处理。

4.6 合并表格

之前处理后的data2.csv导出新表consume.csv，和data1.csv以CardNo字段为主键合并，导出新表grade18.csv。data3.csv在本题没有用到，因此这里就不做处理。

• 问题一的分析与求解

5.1 问题分析

对于学生的消费行为和食堂的运营状况分析，我们主要从三个角度进行分析：早午晚各食堂就餐人次占比、工作日与休息日就餐时间曲线和学生消费的Pearson线性相关系数。因此我们需要对数据进行划分，做进一步的数据处理和提取，然后开始分析。

5.1.1 早午晚各食堂就餐人次占比

将时间分为早餐、午餐和晚餐三个时间段，选出消费地点Dept在包含“食堂”两个字的消费记录，然后把记录分到对应的时间段，如果不在时间段说明消费的不是正餐，不在记录分析的范围内。然后进行三餐各食堂就餐人次的饼图绘制。假设三餐的运营时间段如表5-1所示：

表5-1 三餐运营时段表

运营时段	时间
早餐	06:00–09:30
午餐	10:30–14:30
晚餐	16:00–22:00

5.1.2 工作日与休息日就餐人数与时间关系

采用工作日的数据处理包，按工作日与休息日对消费记录进行划分，过十分钟为一个时间段进行流量的统计，若某个时间段没有流量，则用0补充缺失时段。因为考虑到食堂在六点以前基本是不开门的，所以这里选取从06:00-24:00的数据。然后以时间为横轴，平均人数位纵轴绘制折线图。

5.1.3 学生消费的Pearson线性相关系数

在5.1.1分析的基础之上，取出消费记录中的消费地点Dept、早/午/晚餐Meal、平均消费额AvgMoney和消费次数Count。利用Pearson积差相关系数计算平均消费额AvgMoney和消费次数Count两个字段的相似程度。皮尔森相关系数计算公式如下：

5.2 问题求解

5.2.1 早午晚各食堂就餐人次占比饼图绘制

绘制三餐就餐人数饼图，具体如下：

图5-1(1)早餐就餐人数对比图

从早餐的角度出发,在第二食堂就餐的人数最多,达到48.8%,几乎占了“半壁江山”,说明第二食堂的早饭最受欢迎,其次是第五食堂和第一食堂,分别达到35.7%和14.9%.两者相加也达到了50.6%,而第三和第四食堂的占比几乎为零。

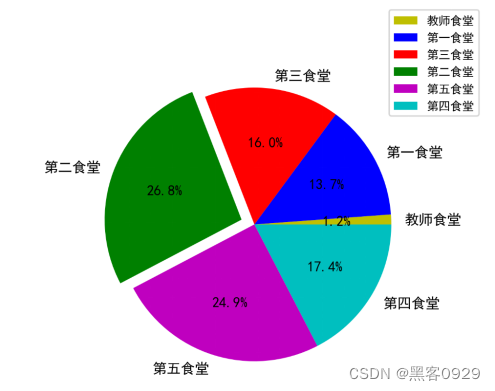
图5-1(2)午餐就餐人数对比图

午餐除教师食堂以外,各食堂的人数占比相对比较均匀。第二食堂和第五食堂的就餐人数相对比较多,分别占比26.8%和24.9%,其余第四、第三食堂分别占比17.4%、16%，第一食堂相对比较落后，只有13.7%的就餐人数。教师食堂可能是因为主要提供教师就餐导致学生很少前往教师食堂就餐，情况比较特殊，只占1.2%。

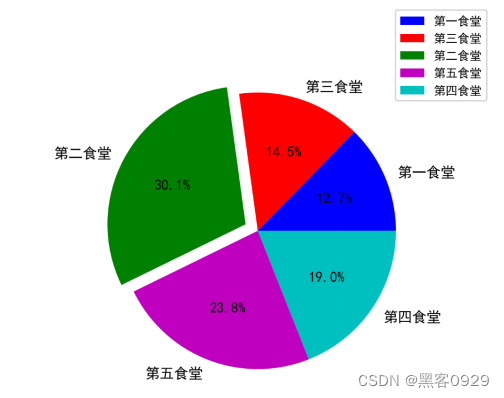
图5-1(3)晚餐就餐人数对比图

晚餐的情况和午餐比较类似，但是晚餐比午餐的差距略大。同样是第二食堂就餐人数最多，占比30.1%，其次是第五食堂和第四食堂，分别占有23.8%和19%的市场份额，最后是第三食堂和第一食堂的情况相对不是非常乐观，只分别占比14.5%和12.7%。

基于以上分析，我们对食堂提出以下几点建议：

（1）第三、第四食堂的早餐几乎无市场份额，可以考虑只开一个窗口或直接取消早餐供应，节省成本；

（2）第一食堂在三餐中都逊色于其他食堂，可以考虑降低价格、增加菜式、改善食堂就餐环境等措施来吸引学生，增加市场竞争力；

（3）教师食堂只在午餐中有市场份额且份额较少，教师食堂可以只提供午餐且供应量满足教师需求即可；

（4）第二和第五食堂在三餐中都比较受欢迎，就餐人数多，可以考虑扩大规模，增开窗口来缓解目前就餐压力；继续改善就餐环境，丰富菜品，吸引更多学生就餐。

5.2.2 工作日与休息日就餐人数与时间曲线绘制

图5-2(1) 工作日就餐人数与时间关系图

工作日的就餐时间曲线图显示出三个就餐高峰，分别对应早中晚三餐的时间且每个食堂都呈现相同的趋势。早餐高峰时段大致开始于7:20，结束于7:50，在7:35左右达到峰值；午餐高峰峰值出现于11：50左右，峰值前后的20分钟就餐人数较多；晚餐的高峰相对比较平缓，前后持续时间约达1.5小时，最高峰出现在18：00左右。除了三个大高峰以外，需要注意的是，图中在9:40，第二食堂会出现一个比较明显的小高峰，而16:20，第二和第五食堂也都出现比较明显的小高峰。

图5-2(2) 休息日就餐人数与时间关系图

休息日与工作日不同在于，休息日的早餐持续时间非常长，同时峰值也相对比较小，而且休息日不同食堂的就餐高峰存在一些差异。早餐就餐人数最多的三个食堂中，第一食堂和第五食堂的峰值分别出现在8:50和7:30，而第二食堂从7:40到9:10几乎都是高峰时段；午餐各个食堂的高峰都在11:30-12:00之间，但是第一食堂会在12:30左右迎来第二波高峰；晚餐的高峰相对午餐而言比较平缓，高峰时段大致位于17:00到18:30之间.总的来说，工作日和休息日相比，从就餐时间分析，午餐和晚餐高峰时间的差异并不明显，但是休息日的早餐高峰持续时间较长；从就餐人数分析，休息日的三餐就餐人数较工作日都明显减少，可能的原因在于休息日大家会选择外出就餐，而不考虑食堂。

基于以上分析，我们对食堂提出以下几点建议：

（1）对于以上数据反映出的三餐就餐高峰，各个食堂根据各自时间提前做好准备，特别是工作日的9:40，第二食堂要做好供应量和食品保温两方面工作，而在16:20晚餐小高峰，其中第二食堂和第五食堂要做好提前提供晚餐的准备；

（2）休息日的三餐就餐人数较工作日大幅减少，食堂注意减少供应，以免造成浪费；

（3）休息日的早餐持续时间较长，食堂要注意对食物进行保温或者分批持续供应。

5.2.3 学生消费的Pearson线性相关系数分析

表5-2 Pearson线性相关系数表

	时间段	线性相关系数
0	午餐	-0.715571
1	早餐	-0.903313
2	晚餐	-0.346169

根据学生消费的Pearson线性相关系数表，我们发现三餐的平均消费金额与消费次数均呈现负的线性相关，且早餐的相关性最大，晚餐的相关性最小。

基于以上分析，我们提出以下相关建议：

（1）第一食堂的早餐消费热度远低于第二和第五食堂，可考虑适当降价来增加市场竞争力，从而提高就餐人数。

• 问题二的模型建立与求解

6.1 问题分析

针对学生的整体校园消费行为，就需要考虑到学生的存储情况与消费情况，因此需要建立一个能有效刻画学生整体消费行为特征的模型。在众多的用户消费模型中，RFM模型是衡量客户消费行为的重要工具。但是考虑到本文的研究对象为学校的学生，最近一次消费这个指标在学校基本是天天消费，所以没有太大的参考价值。因为学生的消费频繁，可以增加一个储蓄情况的指标。故我们引入DFM模型，对学生的消费行为进行刻画，并基于DFM模型对学生进行K-Means++聚类。

6.2 模型建立

在RFM模型的基础上，对其进行改造，得到DFM模型，通过K-means聚类法对学生群体进行分类。

6.2.1 DFM模型介绍

在校园活动中，每个学生的消费行为不同，需要寻找一种工具来判定学生的经济状况。本文为学生的消费情况建立一个能够刻画学生经济状况的DFM数学模型。它以会员关系领域广泛用来衡量会员价值和描述会员行为的RFM模型为基础，拓展优化而成。DFM模型有四个指标，指标含义如下：

• D（Deposit）

D表示学生月平均余额。余额决定着学生能否继续进行消费，在评价学生的整体消费行为中是不可缺少的一项指标。某一时刻的余额高低只能说明某一时刻的经济状况，而学生的消费周期基本上是以月作为单位的，平均一个月的余额，可以大致掌握学生的经济状况。D指标主要刻画了学生的消费基础。

• F（Frequency）

F表示学生在一个月内的消费频率，消费频率越高的学生，一般认为经济状况不会太差消费频率低的学生会受到经济状况的影响而限制消费。F指标主要刻画了学生的消费热度。

• M（Monetary）

M表示学生当月消费的总额，消费总额是所有消费行为的支柱，直接反映了学生的消费能力。M指标主要刻画了学生的消费能力。

DFM模型以上述三个指标为替代变量，通过指标标准化来进行均值聚类分析，将学生分成不同的类别。

6.2.2 D、F、M值的标准化

对各属性进行规格化变换，规格化变换又称为极差正规比变换，是从数据矩阵中的每一个变量最大值和最小值，并用最大值减去最小值得出极差。然后用每一个原始数据减去该变量中的最小值，再除以极差，即得到规格化数据，标准化公式为：

6.2.3 K-Means的改进算法K-Means++

6.3 问题求解

6.3.1 创建特征数据集

提取消费记录中非公共消费的记录，比如水电费之类的消费。这里选取了食堂和超市的消费，因为大学生的大部分个人消费地点都是在这两类地点。选取卡号、月平均余额、月总消费额和月消费频率四个字段，并将消费频率低于30次的数据作为异常数据删除。

表6-1 消费特征表

	CardNo	AvgSurplus	TotalConsume	Freq
0	9	52.56	110.90	45
4	58	179.18	119.90	37
12	4462	44.12	190.10	54
…	…	…	…	…
8334	186148	65.94	114.90	47
8335	186149	56.83	119.50	36
8336	186150	79.17	275.30	49

6.3.2 通过Elbow Method求K-Means++最佳k值

当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大。而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以 SSE 的下降幅度会骤减，随着k值的继续增大而趋于平缓。

图6-1 Elbow Method的SSE-K关系折线图

将每个簇的质点与簇内样本点的平方距离误差和称为畸变程度，那么，对于一个簇，它的畸变程度越低，代表簇内成员越紧密，畸变程度越高，代表簇内结构越松散。畸变程度会随着类别的增加而降低，但对于有一定区分度的数据，在达到某个临界点时畸变程度会得到极大改善，之后缓慢下降，这个临界点就可以考虑为聚类性能较好的点。通过上图分析，最佳的K值在6左右。

6.3.3 数据标准化并聚类可视化

根据上述的分析，创建K-means++模型，将数据标准化，并以三维散点图的形式可视化模型的效果。

图6-2 K-Means++聚类模型散点图

如图6-2所示，根据三维散点图，我们对0-5类学生的消费特征进行分析与总结，总结如下：

（1）0类学生呈现出主要的特征是平均存储少，但是总消费和消费频率都较高，可初步判定为高消费能力人群；

（2）1类学生在图中占少数，可能是部分极端消费的人群；

（3）2类学生分布较分散，三项指标都在平均左右，因此推测是中低等消费人群；

（4）3类学生分布比较密集，总体呈现三低的特征，即平均存储少、总消费少、消费频率低，可初步判定为低消费能力人群；

（5）4类学生呈现出比较高的平均存储和较高的消费频率，总消费也较高，分布比较分散，可以初步判定为广大的中等消费人群；

（6）5类学生最主要特征为总消费非常多，消费频率比较低。

• 问题三的模型建立与求解

7.1 问题分析

为了判断学生的经济状况，问题二使用的聚类方法虽然可以大致确定一个学生的消费水平，但是误差比较大，而且无法得出更多有用的信息，我们希望可以通过数据，来给学生下更加精细的划分，我们就以上题中选出的那最有可能包含需要补助学生的信息的数据集为输入数据，在DFM模型的基础上使用AHP算法进行打分，为学校判定经济状况提供更加可靠的数据。

7.2 模型建立

层次分析法(Analytic Hierarchy Process, AHP)是由美国运筹学家、匹兹堡大学教授Saaty T.L. 提出的一种将决策有关的元素分解成目标、准则、方案等层次，在此基础上进行定量和定性分析的决策方法。常被运用于多目标、多准则、多要素、多层次的非结构化的复杂决策问题上，特别是战略决策问题，可以较好地解决多要素相互关联、相互制约的复杂系统的评价。

7.2.1 定义成对比较矩阵

假设一共有n个因素，要比较每个因素的优劣，引入成对比较矩阵的概念。定义矩阵:

表7-1 AHP算法中关于aij的取值建议

7.2.2 层次排序算法

层次单排序就是把本层所有各元素对上一层来说，排列出评价顺序，核心在于计算最大特征向量，常用的有和积法、方根法。

层次总排序是利用层次单排序的计算结果，进一步综合出对更上一层次的优劣顺序。计算方法和层次单排序一样，所以我们下面只介绍一遍算法的流程。

层次单排序和层次总排序两者加在一起就是层次排序算法。以和积法为例，介绍一下算法的流程

虽然已经有了一套计算方法，但是问题是我们并不能认为输入的判断矩阵全都能符合成对比较矩阵的定义，因此，我们引入一致性检验的概念。

7.2.3 一致性检验

7.3 问题求解

图7-1 各分数人数占比图

根据所得结果，我们对学校判定学生的经济状况并给予补助提供以下建议:

首先在总共大概有8000+的学生，其中相对贫困的人大概有2000+，在这2000+的人当中，根据评分结果， 5分的可以认为是K-Means模型的失误，被划分到了这个区间中，另外四分的比例也比较高，如果也算到最后的补助人口中，补助的比例过高，所以一个比较合理的建议是，选择评分为1、2、3分的进行补助。

梯度补助策略，对于不同分值的人，可以调整金额，比如，1分的人比较少，但是他们是最困难的学生，可以多给他们补助，而2分和3分的人比较多，相对来说他们也没1分的人更加需要这笔补助，所以可以相对来说拿的少一点。

• 模型的评价及推广

8.1 模型的优点

（1）K-Means算法在分类中算是收敛速度比较快的，外加上我们使用的K-Means++由于对初始值做了优化，导致收敛速度更加快。

（2）无论是第二题的K-Means和第三题的AHP都相当简单，易于解释和理解。

（3）AHP每个层次中的每个因素对结果的影响程度都是量化的，非常清晰明确。

8.2 模型的缺点

（1）K-Means对噪声(异常值)比较铭感，所以我们花了很多时间去研究如何洗数据。

（2）K-Means需要提前确定K值，这非常麻烦，有时候还要在大篇幅的程序代码中寻找需要修改的地方

（3）K-Means的输出并不是很稳定，所以每次跑下来的结果都会有一点点差异。

（4）AHP有一个很致命的缺点，我们必须给定一个评价的策略才能让算法去求最优的结果，这导致了一旦策略不够优秀，AHP的结果不准确。也就是受到主观的影响很重。

（5）AHP中一旦一致性比较失败了，那么程序就会失败。

主要代码：

import streamlit as st
import pandas as pd
import time
from PIL import Image
import datetime
from streamlit.components.v1 import html
# from sklearn.metrics import confusion_matrix, roc_auc_score


js_code = '''
$(document).ready(function(){
    $("div[data-testid=stToolbar]", window.parent.document).remove()
});
'''
# 因为JS不需要展示，所以html宽高均设为0，避免占用空间，且放置在所有组件最后
# 引用了JQuery v2.2.4
html(f'''<script src="https://cdn.bootcdn.net/ajax/libs/jquery/2.2.4/jquery.min.js"></script>
    <script>{js_code}</script>''',
     width=0,
     height=0)
# def dat(data):
#     data_k = data.reset_index()
#     try:
#         aa = roc_auc_score(data_k['label'],data_k['proba'])
#     except:
#         aa = None
#     return aa

tab1, tab2 = st.tabs(["性别预测", "疾病预测"])

with tab1:

    st.markdown(
        """
        ## 性别预测作业系统
        ###
        """
    )
    st.markdown(
        """
        #### 提交作业
        """
    )


    now = datetime.datetime.now().replace(microsecond=0)+ datetime.timedelta(hours=8)
    df = pd.read_csv('./gongc/test_label.csv')
    data = pd.read_csv('./gongc/111.csv')
    # label_t = df['gender']
    # 创建file_uploader组件
    uploaded_file = st.file_uploader("请依据示例文件提交csv文件，命名需使用自己的姓名", type={"csv", "txt"},key ='1')
    if uploaded_file is not None:
        try:
            spectra = pd.read_csv(uploaded_file)
            # spectra.columns = ['user_id', 'coupon_id', 'date_received', 'proba']
            start_message = st.empty()
            time.sleep(0.5)
            start_message.caption('提交成功，正在评估中，请等待一段时间!!!:coffee::coffee::coffee:')
            if (df['user_id'] == spectra['user_id']).sum() == len(df):
                spectra['label'] = df['gender']
                sc = (spectra['label'] == spectra['gender']).mean()
                # sc = spectra[['coupon_id', 'proba', 'label']].groupby('coupon_id').apply(dat).mean()
                time.sleep(1.5)
                start_message.caption('评估完成!!!:blossom::blossom::blossom:')
                time.sleep(2)
                start_message.empty()
                st.balloons()
            else:
                sc = 0.5
                time.sleep(3)
                start_message.error('提交错误，请注意提交格式', icon="🚨")
                time.sleep(3)
                start_message.empty()

            name = uploaded_file.name.split('.')[0]
            # st.write(name)
            st.write('准确率：', round(sc,2))
            # st.write('排名为：')
            data1 = {'name': [name], 'score': [round(sc,2)], 's_time': [now]}
            data1 = pd.DataFrame(data1)
            data = pd.concat([data, data1])
            data['s_time'] = pd.to_datetime(data['s_time'])
            # data['score'] = round(data['score'],2)
            data = data.sort_values(by=['score', 's_time'], ascending=[False, True])
            data = data.reset_index(drop=True)
            data = data.drop_duplicates(subset='name',keep = 'first')
            # st.write(data)
            data.to_csv('./gongc/111.csv', index=False)
            data['rank'] = data['score'].rank(method='min',ascending=False)
            st.write('排名为：',int(data[(data['name'] == name)]['rank'].values))



        except:
            st.error('导入文件不规范，请按照示例文件格式修改后再进行上传文件', icon="🚨")
            image = Image.open('./gongc/ces.png')
            st.image(image, caption='请查看示例文件')

        with st.expander("查看排行榜"):
            st.write(data)


            def convert_df(df):
                return df.to_csv().encode('utf-8')


            csv = convert_df(data)
            st.download_button(
                label='下载排行榜',
                data=csv,
                file_name='排行榜数据1.csv',
                key='14'
            )

with tab2:
   # st.image("https://static.streamlit.io/examples/dog.jpg", width=200)
   st.markdown(
       """
       ## 疾病预测作业系统
       ###
       """
   )
   st.markdown(
       """
       #### 提交作业
       """
   )

   now = datetime.datetime.now().replace(microsecond=0) + datetime.timedelta(hours=8)
   df = pd.read_csv('./gongc/AD_CN_label.csv')
   data = pd.read_csv('./gongc/222.csv')
   label_t = df['label']
   # 创建file_uploader组件
   uploaded_file = st.file_uploader("请依据示例文件提交csv文件，命名需使用自己的姓名", type={"csv", "txt"},key ='2')
   if uploaded_file is not None:
       try:
           spectra = pd.read_csv(uploaded_file)
           # spectra.columns = ['user_id', 'coupon_id', 'date_received', 'proba']
           start_message = st.empty()
           time.sleep(0.5)
           start_message.caption('提交成功，正在评估中，请等待一段时间!!!:coffee::coffee::coffee:')
           if (df['name'] == spectra['name']).sum() == len(df):
               spectra['gender'] = df['label']
               sc = (spectra['label'] == spectra['gender']).mean()
               # sc = spectra[['coupon_id', 'proba', 'label']].groupby('coupon_id').apply(dat).mean()
               time.sleep(1.5)
               start_message.caption('评估完成!!!:blossom::blossom::blossom:')
               time.sleep(2)
               start_message.empty()
               st.balloons()
           else:
               sc = 0.5
               time.sleep(3)
               start_message.error('提交错误，请注意提交格式', icon="🚨")
               time.sleep(3)
               start_message.empty()

           name = uploaded_file.name.split('.')[0]
           # st.write(name)
           st.write('准确率：', round(sc, 2))
           # st.write('排名为：')
           data1 = {'name': [name], 'score': [round(sc, 2)], 's_time': [now]}
           data1 = pd.DataFrame(data1)
           data = pd.concat([data, data1])
           data['s_time'] = pd.to_datetime(data['s_time'])
           # data['score'] = round(data['score'],2)
           data = data.sort_values(by=['score', 's_time'], ascending=[False, True])
           data = data.reset_index(drop=True)
           data = data.drop_duplicates(subset='name', keep='first')
           # st.write(data)
           data.to_csv('./gongc/222.csv', index=False)
           data['rank'] = data['score'].rank(method='min', ascending=False)
           st.write('排名为：', int(data[(data['name'] == name)]['rank'].values))

       except:
           st.error('导入文件不规范，请按照下面的例子再进行上传文件', icon="🚨")
           image = Image.open('./gongc/ces2.png')
           st.image(image, caption='请查看示例文件')
       with st.expander("查看排行榜"):
           st.write(data)


           def convert_df(df):
               return df.to_csv().encode('utf-8')


           csv = convert_df(data)
           st.download_button(
               label='下载排行榜',
               data=csv,
               file_name='排行榜数据2.csv',
               key='13'
           )

# with tab3:
#
#    # st.image("https://static.streamlit.io/examples/owl.jpg", width=200)
#    # st.image("https://static.streamlit.io/examples/dog.jpg", width=200)
#    st.markdown(
#        """
#        ## 电商客流量预测作业系统
#        ###
#        """
#    )
#    st.markdown(
#        """
#        #### 提交作业
#        """
#    )
#
#    now = datetime.datetime.now().replace(microsecond=0) + datetime.timedelta(hours=8)
#    df = pd.read_csv('./gongc/sc3.csv')
#    data = pd.read_csv('./gongc/333.csv')
#    label_t = df['label']
#    # 创建file_uploader组件
#    uploaded_file = st.file_uploader("请提交仅含[label]列的csv文件，命名需使用自己的姓名", type={"csv", "txt"}, key='3')
#    if uploaded_file is not None:
#        try:
#            spectra = pd.read_csv(uploaded_file)
#            label_p = spectra['label']
#            sc = sum(label_t == label_p) / len(label_t)
#            name = uploaded_file.name.split('.')[0]
#            # st.write(name)
#            st.write('准确度为：', round(sc,2))
#            # st.write('排名为：')
#            data1 = {'name': [name], 'score': [sc], 's_time': [now]}
#            data1 = pd.DataFrame(data1)
#            data = pd.concat([data, data1])
#            data['s_time'] = pd.to_datetime(data['s_time'])
#            data['score'] = round(data['score'], 2)
#            data = data.sort_values(by=['score', 's_time'], ascending=[False, True])
#            data = data.reset_index(drop=True)
#            data = data.drop_duplicates(subset='name', keep='first')
#            # st.write(data)
#            data.to_csv('./gongc/333.csv', index=False)
#            data['rank'] = data['score'].rank(method='min', ascending=False)
#            st.write('排名为：', int(data[(data['name'] == name)]['rank'].values))
#            st.balloons()
#
#
#        except:
#            st.error('导入文件不规范，请按照下面的例子再进行上传文件', icon="🚨")
#            image = Image.open('./gongc/ces.jpg')
#            st.image(image, caption='仅有一列label的csv文件')
#        with st.expander("查看排行榜"):
#            st.write(data)
#
#
#            def convert_df(df):
#                return df.to_csv().encode('utf-8')
#
#
#            csv = convert_df(data)
#            st.download_button(
#                label='下载排行榜',
#                data=csv,
#                file_name='排行榜数据.csv',
#                key = '12'
#            )