七、优化算法

机器学习算法 = 模型表征 + 模型评估 + 优化算法。
其中，优化算法所做的事情就是在模型表征空间中找到模型评估指标最好的模型。不同的优化算法对应的模型表征和评估指标不尽相同，比如经典的支持向量机对应的模型表征和评估指标分别为线性分类模型和最大间隔，逻辑回归对应的模型表征和评估指标则分别为线性分类模型和交叉熵。 随着大数据和深度学习的迅猛发展，在实际应用中面临的大多是大规模、高度非凸的优化问题，这给传统的基于全量数据、凸优化的优化理论带来了巨大的挑战。

有监督学习的损失函数

机器学习算法的关键一环是模型评估，而损失函数定义了模型的评估指标。 可以说，没有损失函数就无法求解模型参数。不同的损失函数优化难度不同，最终得到的模型参数也不同，针对具体的问题需要选取合适的损失函数。

分类问题

0-1损失函数

对二分类问题，Y={1,−1}，最自然的损失函数是0-1损失，即预测值和目标值不相等为1， 否则为0。该损失函数能够直观地刻画分类的错误率，但是由于其非凸、非光滑的特点， 使得算法很难直接对该函数进行优化。

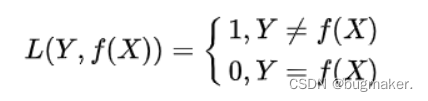
指数损失函数

exponential loss为AdaBoost中使用的损失函数，使用exponential loss能比较方便地利用加法模型推导出AdaBoost算法 。然而其和squared loss一样，对异常点敏感，不够robust。

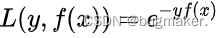
交叉熵损失函数（对数损失函数的特例）：

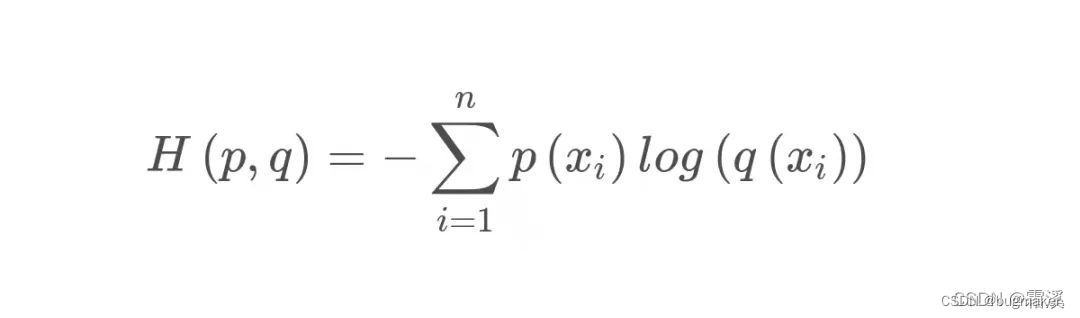
其中P(X)是样本分布的概率，q（ x）是预测函数。在机器学习中P(X)通常是已知的，因此P(X)可以用y来表示。
对二分类而言，H(p,q)=

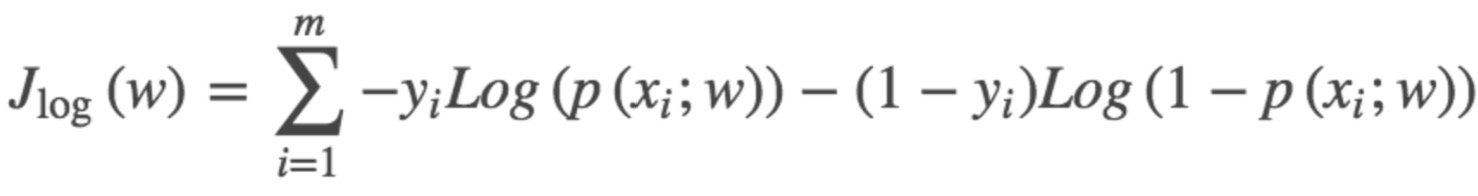
交叉熵损失函数也是0-1损失函数的光滑凸上界。

回归问题

平方损失函数

对于回归问题，最常用的损失函数是平方损失函数

绝对损失函数

平方损失函数是光滑函数，能够用梯度下降法进行优化。然而，当预测值距离真实值越远时，平方损失函数的惩罚力度越大，因此它对异常点比较敏感。为了解 决该问题，可以采用绝对损失函数

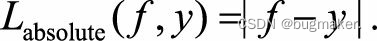
huber损失函数

绝对损失函数相当于是在做中值回归，相比做均值回归的平方损失函数，绝对损 失函数对异常点更鲁棒一些。但是，绝对损失函数在f=y处无法求导数。综合考虑可导性和对异常点的鲁棒性，可以采用Huber损失函数：

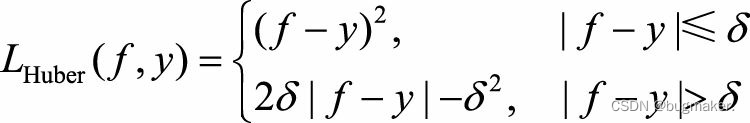
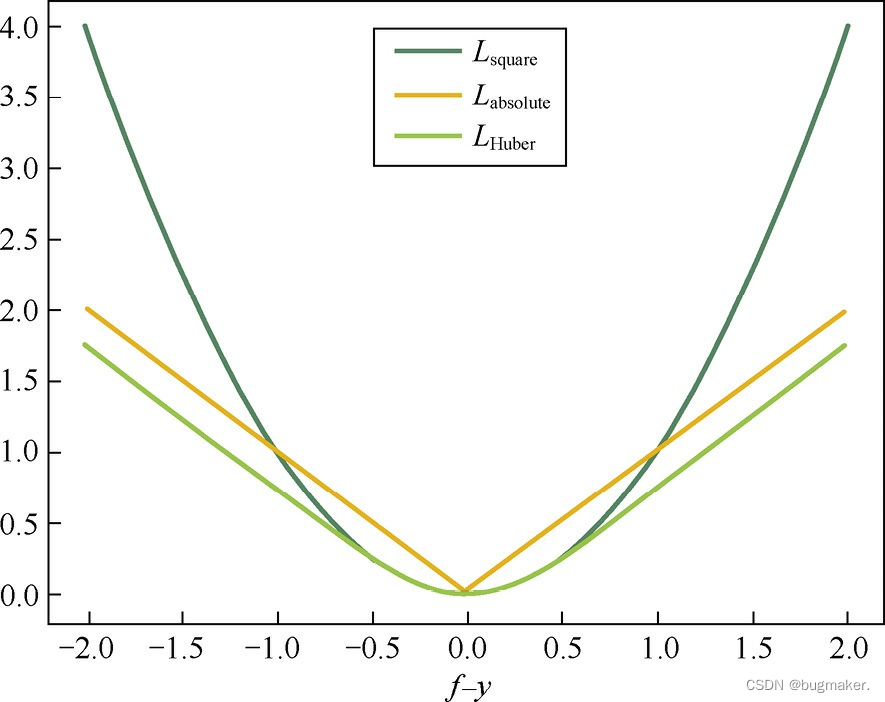
Huber损失函数在|f−y|较小时为平方损失，在|f−y|较大时为线性损失，处处可导， 且对异常点鲁棒。这三种损失函数的曲线如图所示。

机器学习中的优化问题

机器学习中的优化问题，哪些是凸优化问题，哪些是非凸优化问题？请各举一个例子。

逻辑回归对应的优化问题就是凸优化问题、主成分分析对应的优化问题是非凸优化问题。

经典优化算法

针对不同的优化问题和应用场景，研究者们提出了多种不同的求解算法，并逐渐发展出了有严格理论支撑的研究领域——凸优化。在这众多的算法中，有几种经典的优化算法是值得被牢记的，了解它们的适用场景有助于我们在面对新的优化问题时有求解思路。
经典的优化算法可以分为直接法和迭代法两大类。
直接法，顾名思义，就是能够直接给出优化问题最优解的方法。这个方法听起来非常厉害的样子，但它不是万能的。直接法要求目标函数需要满足两个条件。
第一个条件是，L(·)是凸函数。若L(·)是凸函数，那么θ是最优解的充分必要条 件是L(·)在θ处的梯度为0。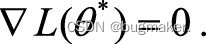
第二个条件是，上式有闭式解。

直接法要满足的这两个条件限制了它的应用范围。因此，在很多实际问题中，会采用迭代法。迭代法就是迭代地修正对最优解的估计。假设当前对最优解的估计值为θt，希望求解优化问题

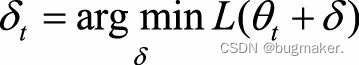
迭代法又可以分为一阶法和二阶法两类。一阶法对函数L(θt+δ)做一阶泰勒展开，二阶法对函数L(θt+δ)做二阶泰勒展开。二阶法也称为牛顿法，Hessian矩阵就是目标函数的二阶信息。二阶法的收敛速度一般要远快于一阶法，但是在高维情况下，Hessian矩阵求逆的计算复杂度很 大，而且当目标函数非凸时，二阶法有可能会收敛到鞍点（Saddle Point）。

梯度下降法：

经典的优化方法，如梯度下降法，在每次迭代时需要使用所有的训练数据， 这给求解大规模数据的优化问题带来了挑战。如何克服这个挑战，对于掌握机器学习，尤其是深度学习至关重要。

随机梯度下降

经典的梯度下降法采用所有训练数据的平均损失来近似目标函数，因此，经典的梯度下降法在每次对模型参数进行更新时，需要遍历所有的训练数据。这需要很大的计算量，耗费很长的计算时间，在实际应用中基本不可行。
为了解决该问题，随机梯度下降法（Stochastic Gradient Descent，SGD）用单个训练样本的损失来近似平均损失，因此，随机梯度下降法用单个训练数据即可对模型参数进行一次更新，大大加快了收敛速率。该方法也非常适用于数据源源不断到来的在线更新场景。 但是，随机梯度下降法并不是万金油，有时候反而会成为一个坑。

小批量梯度下降

为了降低随机梯度的方差，从而使得迭代算法更加稳定，也为了充分利用高度优化的矩阵运算操作，在实际应用中我们会同时处理若干训练数据，该方法被称为小批量梯度下降法（Mini-Batch Gradient Descent）。
对于小批量梯度下降法的使用，有以下三点需要注意的地方。
（1）如何选取参数m？在不同的应用中，最优的m通常会不一样，需要通过调参选取。一般m取2的幂次时能充分利用矩阵运算操作，所以可以在2的幂次中挑 选最优的取值，例如32、64、128、256等。
（2）如何挑选m个训练数据？为了避免数据的特定顺序给算法收敛带来的影响，一般会在每次遍历训练数据之前，先对所有的数据进行随机排序，然后在每次迭代时按顺序挑选m个训练数据直至遍历完所有的数据。
（3）如何选取学习速率α？为了加快收敛速率，同时提高求解精度，通常会采用衰减学习速率的方案：一开始算法采用较大的学习速率，当误差曲线进入平台期后，减小学习速率做更精细的调整。最优的学习速率方案也通常需要调参才 能得到。
综上，通常采用小批量梯度下降法解决训练数据量过大的问题。每次更新模型参数时，只需要处理m个训练数据即可，其中m是一个远小于总数据量M的常数，这样能够大大加快训练过程。

随机梯度下降法失效的原因：

传统梯度下降法的每一步都把整个训练集载入进来进行计算，时间花费和内存开销都非常大，无法应用于大数据集、大模型的场景。相反，随机梯度下降法则放弃了对梯度准确性的追求，每步仅仅随机采样少量样本来估计当前梯度，计算速度快，内存开销小。但由于每步接受的信息量有限，随机梯度下降法对梯度的估计常常出现偏差，造成目标函数曲线收敛得很不稳定，伴有剧烈波动，有时甚至出现不收敛的情况。

但对随机梯度下降法来说，可怕的是山谷和鞍点两类地形。 山谷顾名思义就是狭长的山间小道，左右两边是峭壁；鞍点的形状像是一个马鞍，一个方向上两头翘，另一个方向上两头垂，而中心区域是一片近乎水平的平地。在山谷中，准确的梯度方向是沿山道向下，稍有偏离就会撞向山壁，而粗糙的梯度估计使得它在两山壁间 来回反弹震荡，不能沿山道方向迅速下降，导致收敛不稳定和收敛速度慢。在鞍点处，随机梯度下降法会走入一片平坦之地。同样，在梯度近乎为零的区域，随机梯度下降法无法准确察觉出梯度的微小变化，结果就停滞下来。

解决之道——惯性保持和环境感知

随机梯度下降法的更新公式表示为

其中，当前估计的负梯度−gt表示步子的方向，学习速率η控制步幅。改造的随机梯度下降法仍然基于这个更新公式。

动量方法

为了解决随机梯度下降法山谷震荡和鞍点停滞的问题，我们做一个简单的思维实验。想象一下纸团鞍点处的运动情况，当纸团来到鞍点的一片平坦之地时，还是由于质量小，速度很快减为零。如果换成一个铁球，当沿山谷滚下时，当来到鞍点中心处，铁球会在惯性作用下继续前行，从而有机会冲出这片平坦的陷阱。因此，有了动量方法，模型参数的迭代公式为

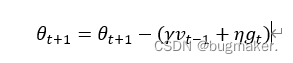
具体来说，前进步伐由两部分组成。一是学习速率η乘以当前估计的梯度gt；二是带衰减的前一次步伐vt−1。这里，惯性就体现在对前一次步伐信息的重利用上。
类比中学物理知识，当前梯度就好比当前时刻受力产生的加速度，前一次步伐好 比前一时刻的速度，当前步伐好比当前时刻的速度。为了计算当前时刻的速度， 应当考虑前一时刻速度和当前加速度共同作用的结果，因此vt直接依赖于vt−1和gt， 而不仅仅是gt。另外，衰减系数γ扮演了阻力的作用。

AdaGrad方法

AdaGrad方法根据不同参数的一些经验性判断，自适应地确定参数的学习速率，不同参数的更新步幅是不同的。 在应用中，我们希望更新频率低的参数可以拥有较大的更新步幅，而更新频率高的参数的步幅可以减小。AdaGrad方法采用“历史梯度平方和”来衡量不同参数的梯度的稀疏性，取值越小表明越稀疏。

Adam方法

Adam方法将上述两个优点集于一身。一方面，Adam记录梯度的一阶矩，即过往梯度与当前梯度的平均，这体现了惯性保持；另一方面，Adam还记录梯度的二阶矩，即过往梯度平方与当前梯度平方的平均，这类似AdaGrad方法，为不同参数产生自适应的学习速率。一阶矩和二阶矩采用类似于滑动窗口内求平均的思想进行融合，即当前梯度和近一段时间内梯度的平均值，时间久远的梯度对当前平均值的贡献呈指数衰减。

L1正则化与稀疏性

L1正则化就是一范数、L2正则化就是二范数。
L1正则化对所有参数的惩罚力度都一样，可以让一部分权重变为零，因此产生稀疏模型，能够去除某些特征（权重为0则等效于去除）。
L2正则化减少了权重的固定比例，使权重平滑。L2正则化不会使权重变为0（不会产生稀疏模型），所以选择了更多的特征。

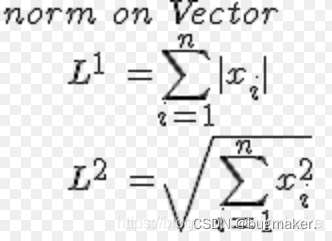
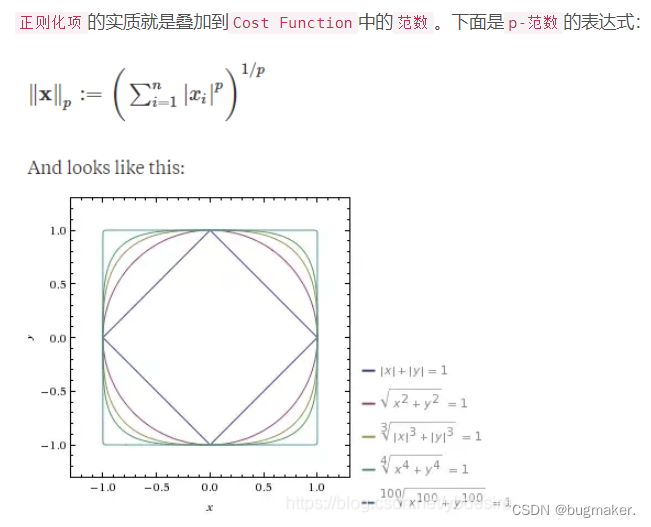
L1正则化使得模型参数具有稀疏性的原理是什么？

在二维的情况下，黄色的部分是L2和L1正则项约束后的解空间，绿色的等高线是凸优化问题中目标函数的等高线，如图所示。由图可知，L2正则项约束后的解空间是圆形，而L1正则项约束的解空间是多边形。 显然，多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。

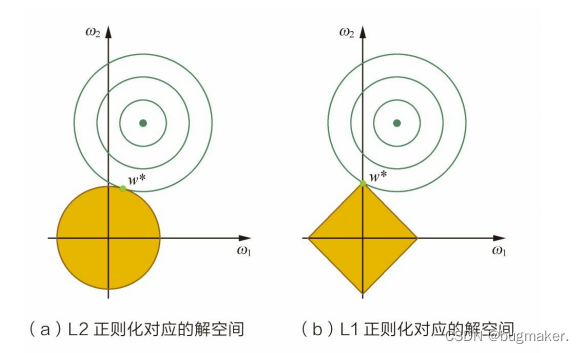
L2正则化相当于为参数定义了一个圆形的解空间（因为必须保证L2范数不能大于m），而L1正则化相当于为参数定义了 一个棱形的解空间。如果原问题目标函数的最优解不是恰好落在解空间内，那么 约束条件下的最优解一定是在解空间的边界上，而L1“棱角分明”的解空间显然更 容易与目标函数等高线在角点碰撞，从而产生稀疏解。