本文介绍了矩形卷积和非对称卷积核在卷积神经网络中如何影响输出特征图的尺寸。通过公式详细阐述了不同参数如步幅、Padding和空洞值对特征图尺寸计算的影响，适用于计算机视觉和深度学习领域的应用。
矩形卷积和非对称卷积核，卷积后的特征图尺寸计算其实原理是一样的。
矩形卷积
如果输入图像是正方形，尺寸为WxW，卷积核尺寸为FxF，步幅为S，Padding使用P，经过该卷积层后输出的特征图尺寸为NxN：
如果输入图像是矩形，尺寸为WxH，卷积核的尺寸为FxF，步幅为S，图像深度(通道数)为C，Padding使用P，则：
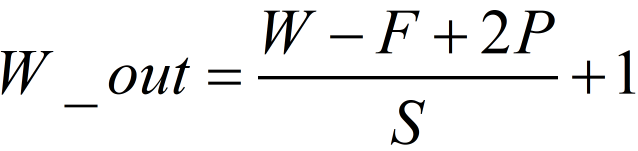
非对称卷积核卷积：
此处只例举输入图像是正方形的情况。设输入图像尺寸为WxW，卷积核尺寸为ExF，步幅为S，Padding为P，卷积后的特征图尺寸为：
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
