双机调度解决算法

题目：双机调度。n项任务，加工时间分别是正整数t1,t2,…tn，现有两台机器，从0时刻安排加工这些任务，只要有待加工任务，任何机器不得闲置，若直到T时刻完成所有任务，则总加工时间是T。

方法一：动态规划

一、解决思路
n个任务，每个任务花费的时间为ti,两台机器记为A、B，设两台机器的加工时间为T1,T2,有以下两个约束条件：，。将问题转化为把t1,t2,…tn划分为两部分，一部分之和是T1，另一部分之和为T2，使得最小，也就是t1和t2的差尽可能小,让T1和T2都尽可能接近背包的一半。
那么对于任意一个任务来说，都有两个状态，即A机器执行和B机器执行，可以将这两种状态分别记为0和1，用调度函数f(i)={0,1}表示第i项任务应该在哪台机器上执行。所以可以将其转化为0,1背包问题。
dp[i][j]表示前i个任务在一个机器上的执行时间不超过j的情况下的最优解，所以j的范围是0—T/2。当j<t[i]时，任务i无法执行，dp[i][j]=dp[i-1][j]；当j>=t[i]时，dp[i][j]=max{dp[i-1][j],dp[i-1][j-t[i]]+t[i]}。
对于输出方案，考虑在dp过程中遇到答案更新就标记这个位置，即标记flag[i][j]=1，表示第i件任务在当背包容量为j时被选取了。然后就可以对包的容量V从大到小遍历，同时对物品i也从大到小遍历，对于某一对i，j，如果flag[i][j]=1，此时就说明第i件任务被选取，然后为了继续向下回溯，此时j=j-t[i]，直到j=0。
二、设计过程
输入：任务数，分别各个任务需要处理的时间
输出：计算过程中的dp二维数组，分配情况及最短处理时间
1、01背包部分：max(dp1[n][V], (sum - dp1[n][V]))即最小总加工时间。

 int V = sum / 2
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            if (j >= t[i])
            {
                if (dp1[i][j] < dp1[i - 1][j - t[i]] + t[i])
                {
                    dp1[i][j] = dp1[i - 1][j - t[i]] + t[i];
                    flag[i][j] = 1;
                }
            }
        }
    }

2、输出方案部分：ans[i]就是任务的分组

  for (int i = n, j = V; i >= 1 && j > 0; i--) {
        if (flag[i][j] == 1) {
            ans[i] = 1;
            j -= t[i];
        }
    }

3、算法时间复杂度为O（V*n）。

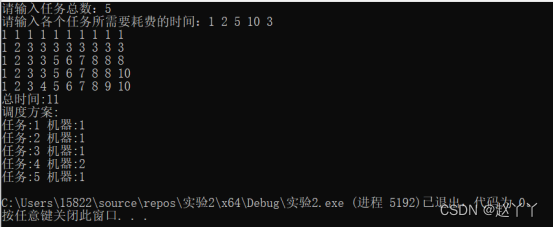
结果分析：输入待加工的任务数为5，每个任务所对应的加工时间{1,2,5,10,3}，输出计算过程中dp二维数组的内容，最短处理时间为11以及调度方案，将任务1,4分配给第一台机器，任务2,3,5分配给第二台机器。
三、改进方法
对空间进行进一步优化，即使用滚动数组将二维优化到一维。dp[j]表示对于体积为j的背包，从所有任务中选出最大体积，转移方程为：
dp[j]=max{dp[j],dp[j-t[i]]+t[i]}(j≥t[i])

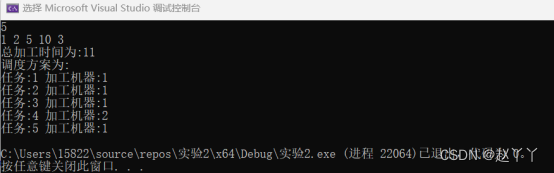
对于改进后的方法，得到的调度方案及加工时间相同。
四、源码

int main()
{
    memset(dp1, 0, sizeof dp1);
    memset(flag, 0, sizeof flag);
    printf("请输入任务总数：");
    cin >> n;
    printf("请输入各个任务所需要耗费的时间：");
    for (int i = 1; i <= n; i++) {
        cin >> t[i];
        sum += t[i];
    }
    int V = sum / 2;

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            if (j >= t[i])
            {
                if (dp1[i][j] < dp1[i - 1][j - t[i]] + t[i])
                {
                    dp1[i][j] = dp1[i - 1][j - t[i]] + t[i];
                    flag[i][j] = 1;
                }
                else {
                    dp1[i][j] = dp1[i - 1][j];
                }
            }
            else {
                dp1[i][j] = dp1[i - 1][j];
            }
            printf("%d ", dp1[i][j]);
        }
        printf("\n");
    }
    for (int i = n, j = V; i >= 1 && j > 0; i--) {
        if (flag[i][j] == 1) {
            ans[i] = 1;
            j -= t[i];   
        }
    }
    cout << "总时间:";
    cout << max(dp1[n][V], (sum - dp1[n][V])) << endl;
    cout << "调度方案:" << endl;
    for (int i = 1; i <= n; i++) {
        cout << "任务:" << i << " " << "机器:" << ans[i] + 1 << endl;
    }
}

方法二：贪心算法

一、解题思路
让最长处理时间的作业优先，即把处理时间最长的作业分配给最先空闲的机器，这样就可以保证处理时间长的作业优先处理，从而在整体上获得尽可能最短的处理时间。
当任务数大于机器数，即n>m时。首先将这n个作业从大到小排序，然后依此顺序将作业分配给空闲的处理机。也就是从剩下的作业中，选择需要处理时间最长的，然后依次选择处理时间次长的，直到所有的作业全部处理完毕。如果我们每次是将需要处理时间最短的作业分配给空闲的机器，那么可能就会出现其它所有作业都处理完了只剩所需时间最长的作业在处理的情况，从而延长总加工时间。
二、设计过程
输入：机器数、任务数，分别输入任务ID和需要处理的时间
输出：分配情况及最短处理时间
算法时间复杂度为O（n^2）。

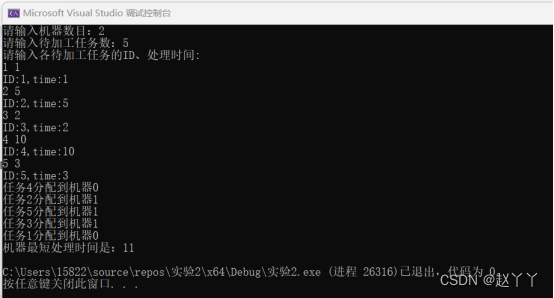
结果分析：输入机器数为2，待加工的任务数为5，每个任务的ID及其所对应的加工时间{1,5,2,10,3}，输出调度方案，将任务1,4分配给第一台机器，任务1,3,5分配给第二台机器，最短处理时间为11。
三、源码

class Time {
public:
	int ID;
	int duration;
};
int main() {
	int m;		//m台机器
	int n;		//n个任务
	int time;	//记录最小处理时间

	cout << "请输入机器数目：";
	cin >> m;

	cout << "请输入待加工任务数：";
	cin >> n;

	int* machine = new int[m];		//记录每个机器的处理时间
	Time* t = new Time[n];		// 记录每个任务的处理时间

	cout << "请输入各待加工任务的ID、处理时间:" << endl;

	for (int i = 0; i < n; i++) {
		cin >> t[i].ID >> t[i].duration;
		cout << "ID:" << t[i].ID << ",time:" << t[i].duration << endl;
	}


	Time tmp;

	for (int i = 0; i < n - 1; i++)
		for (int j = 0; j < n - i - 1; j++)
		{
			if (t[j].duration < t[j + 1].duration)
			{
				tmp = t[j];
				t[j] = t[j + 1];
				t[j + 1] = tmp;
			}
		}

	time = t[0].duration;
	int min;
	int min_pos;

	if (n > m)
	{
		for (int i = 0; i < m; i++)		//每个机器赋值一次
		{
			machine[i] = t[i].duration;
			cout << "任务" << t[i].ID << "分配到机器" << i << endl;
		}


		for (int i = m; i < n; i++)		//对于剩下的n-m个作业，找已经处理的最小时间的机器
		{
			min = machine[0];
			min_pos = 0;

			for (int j = 1; j < m; j++)
			{
				if (machine[j] < min)
				{
					min = machine[j];
					min_pos = j;
				}
			}
			machine[min_pos] += t[i].duration;
			cout << "任务" << t[i].ID << "分配到机器" << min_pos << endl;
			if (time < machine[min_pos])
				time = machine[min_pos];
		}
	}
	cout << "机器最短处理时间是：" << time << endl;
	return 0;
}

方法三：回溯法

一、解题思路
该问题的解空间是一棵排列树。按照回溯法搜索排列树的算法框架，设开始时t=[1,2, … , n]是所给的n个作业的完成时间，则相应的排列树由t[1:n]的所有排列构成。算法搜索至叶子结点，得到一个新的作业调度方案。此时算法适时更新当前最优值和相应的当前最佳调度。若当前扩展结点位于排列树的第（n-1）层，此时算法选择下一个要安排的作业进行搜索且向第(n-2)层回溯，以深度优先方式递归的对相应的子树进行搜索，对不满足上界约束的结点，则剪去相应的子树向第(n-2)层回溯。
二、设计过程
从n个作业中找出有最小完成时间和的作业调度，所以批处理作业调度问题的解空间是一棵排列树。按照回溯法搜索排列树的算法框架，设开始时t=[1,2, … , n]是所给的n个作业的完成时间，则相应的排列树由t[1:n]的所有排列构成。
数组len[]用于存储一组空间解，comp()函数用于计算一个完整调度的完成时间，search()函数用来做搜索，best记录相应的当前最佳作业调度完成时间。
当dep>n时，算法搜索至叶子结点，得到一个新的作业调度方案。此时算法适时更新当前最优值和相应的当前最佳调度。
当dep<n时，若当前扩展结点位于排列树的第（n-1）层，此时算法选择下一个要安排的作业进行搜索且向第(n-2)层回溯，以深度优先方式递归的对相应的子树进行搜索，对不满足上界约束的结点，则剪去相应的子树向第(n-2)层回溯。
对于给定任务的加工时间，给出总加工时间。
回溯法搜索排列树：

void search(int dis, int* count, int* t) {
	if (dis == n) {
		int tmp = copmare();
		if (tmp < ans)
			ans = tmp;
		return;
	}
	for (int i = 0; i < k; i++) {
		count[i] += t[dis];
		if (count[i] < ans)
			search(dis + 1, count, t);
		count[i] -= t[dis];
	}
}

算法时间复杂度为O（n!）。
三、源码

int n = 5, k = 2, ans = 10000;
int count[100];
int t[100] = { 1,5,2,10,3 };
int copmare() {
	int tmp = 0;
	for (int i = 0; i < k; i++)
		if (count[i] > tmp)
			tmp = count[i];
	return tmp;
}
void search(int dis, int* count, int* t) {
	if (dis == n) {
		int tmp = copmare();
		if (tmp < ans)
			ans = tmp;
		return;
	}
	for (int i = 0; i < k; i++) {
		count[i] += t[dis];
		if (count[i] < ans)
			search(dis + 1, count, t);
		count[i] -= t[dis];
	}
}
int main() {
	int i;
	for (i = 0; i < k; i++)
		count[i] = 0;
	search(0, count, t);
	printf("%d\n", ans);
	return 0;
}