图象关于y轴对称是什么意思_【二次函数系列专题】 二次函数图象与系数关系一题多问...

点击上方蓝字关注我们

【二次函数系列专题】

二次函数图象与系数关系一题多问

TSQ中学数学微信：TSQmaths

一、中考解读

二次函数图像与系数的关系在中考中属于高频考点，通常出现在选择题第11题或第12题，作为压轴题出现，难度适中.

考点：主要考查二次函数图像性质、二次函数与一元二次方程的关系以及根与系数的关系、二次函数与不等式之间的关系.

二、解题策略

解题策略：

1. 判断a、b、c的符号，abc的符号.

a的符号的判断根据开口方向：

开口方向向上a>0，

开口方向向下a<0.

b的符号根据对称轴的位置：

当对称轴在y轴左侧b和a的符号相同，

当对称轴在y轴右侧b和a的符号相反.

简称“左同右异”

c的符号根据图像与y轴的交点：

图像与y轴正半轴相交c>0，

图像与y轴负半轴相交c<0.

5.求与x轴另一交点

解题策略：已知一交点，利用两交点关于对称轴对称，求另一交点.

6.已知x比较y的大小关系

解题策略：在对称轴同一侧可根据增减性判断

在对称轴两侧可根据距离对称轴的远近判断

三、典例精讲

问题拓展：

四、问题解答

已知抛物线y₁＝ax²+bx+c(a≠0)的对称轴是直线x＝1，y₂= -2x+6其部分图象如图所示，判断下列说法是否正确：

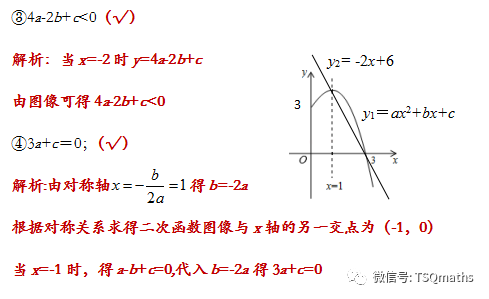
问题拓展：

五、方法总结

学好函数，需要数形结合，利用函数图象就能够清晰地分析函数的性质.而函数图象受函数关系中待定常数的影响，想要分析函数图象，就得讨论函数关系式中常数对函数图象的影响.

一.a的作用

a决定开口方向与开口大小影响抛物线的开口方向和开口大小，

1.a＞0，开口向上，a＜0，开口向下；

2.∣a∣越大，开口越小，∣a∣越小，开口越大；

二．c的作用

c决定抛物线与y轴交点的位置

当x=0，y=c，抛物线与y轴交于(0，c),c决定抛物线与y轴交点的位置。

1.c＞0，与y轴交于正半轴；

2.c＝0过原点；

3.c＜0，与y轴交于负半轴。

三、a,b共同影响对称轴对称轴x=-b/2a,

a,b的值决定了对称轴，也决定了对称轴的位置，

1. 当a,b同号时，对称轴在y轴左边；

2. 当a,b异号时，对称轴在y轴右边。

3. 这个性质可简记为“同左异右”，也可记为“左同右异”。

四．其它a,b,c组合

1.二次函数y=ax²+bx+c当y=0时对应的一元二次方程ax²+bx+c=0当b²-4ac＞0时有两个不相等的实数根，即抛物线与x轴有两个交点；

2.当b²-4ac=0时抛物线与x轴只有一个交点；

3.当b²-4ac＜0时抛物线与x轴没有交点.

五．常用结论

1.a+b+c表示x=1时的函数值；

2.a-b+c表示x=-1时的函数值；

3.4a+2b+c表示x=2时的函数值；

4.9a+3b+c表示x=3时的函数值.

齐心抗疫与你同在 更多精彩内容请关注我们点亮在看，你最好看！