平行四边形面积_一课研究之人教版平行四边形的面积教学设计

向你介绍我是谁

大家好，我是台州市路南小学的徐金芳，是朱乐平名师工作站“一课研究”第6小组成员，很高兴在“一课研究”的微信平台中与您相遇。

本期内容有哪些

听一听：努力做好“理论的实践性解读”与“教学实践的理论性反思”

读一读：《平行四边形的面积》教学设计

想一想：智斗巴依老爷

轻轻松松听听书

节选自郑毓信的《小学数学教师专业成长的“中国道路”》

坚持阅读八分钟

《平行四边形的面积》

教学设计

一、教学内容

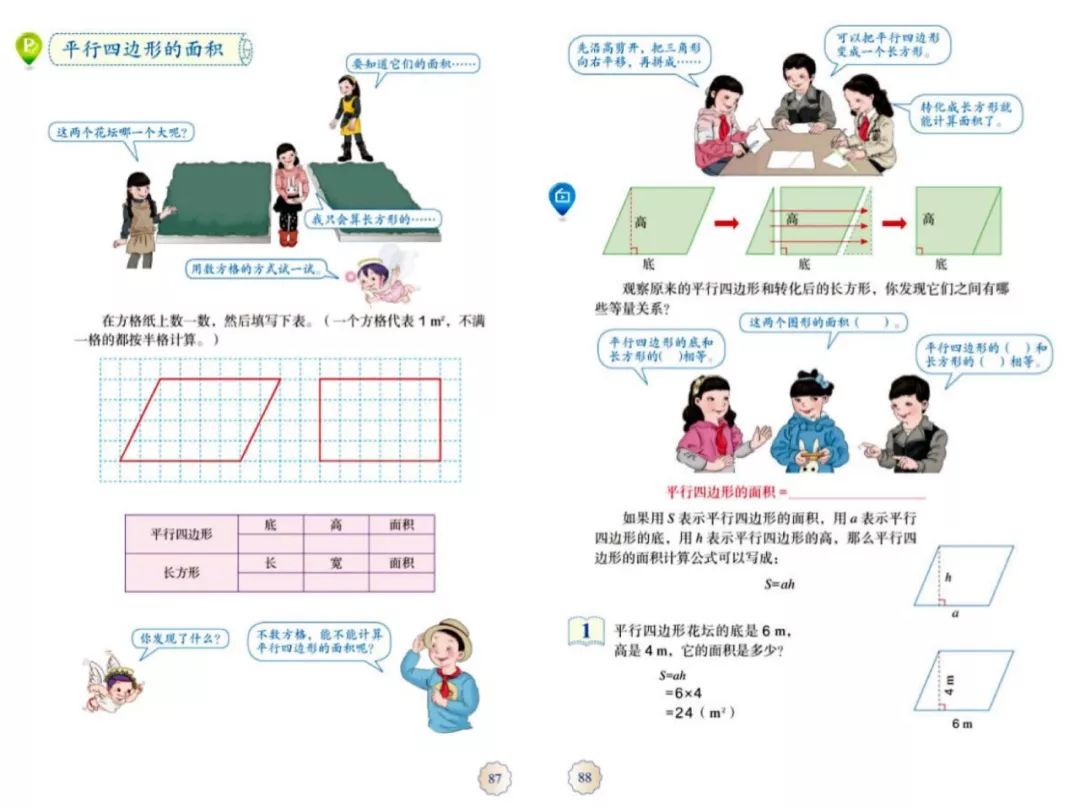
人教版小学数学五年级上册第87、88页

      《平行四边形的面积》是人教版五年级上册“多边形的面积”第一课时的教学内容，是学生运用已有知识推导新的面积公式的起始课，也是后续学习三角形面积、梯形面积的知识基础，本质上是起到了承前启后的重要作用。教材中以推导平行四边形面积公式为主要内容，以学生动手操作验证为探究过程，注重新旧知识间的转化与联系。

二、教学目标

1.经历平行四边形面积的计算公式的探究过程，抽象、概括出平行四边形面积的计算方法。

2.掌握平行四边形面积的计算公式，并能正确地应用公式计算平行四边形的面积。

3.在推导和探究过程中，体会转化的数学思想方法，发展学生的空间观念。

三、教学重难点

教学重点：掌握和运用平行四边形面积计算公式，能正确计算平行四边形面积。

教学难点：平行四边面积计算公式的推导过程。

四、教学过程

1. 拼组图形，渗透转化

师：你能用这三个图形拼出哪些平面图形？

师：在这4个图形的变化中，你们发现了什么？(什么变了，什么没有变)

生：它们都是由同样的图形拼成的，形状变了，面积没有变。

师：对啊，虽然这些图形的形状变了，面积没有变。这就是一种图形之间的转化，你们还在哪里用到过转化？

  [设计意图：通过图形的拼组，感受拼组过程中图形的变和不变，渗透图形之间的转化。]

2.  直接导入，验证猜想

1.联系旧知，引发猜测。

(1)依次出示正方形、长方形、平行四边形，计算面积。

生：正方形5×5，长方形7×5，平行四边形7×5，7×3

(2)猜测平行四边形的面积：7×5或者7×3

师：你是怎么想的？(针对7×5)

生：长方形的面积等于长乘宽，所以我猜平行四边形的面积也这样。

师：所以你认为平行四边形的面积时这两条边相乘。还有不同的猜想吗？

生：应该用底乘高去计算。课件出示高，7×3

师：两种猜想，产生两种不同的结果，到底哪一个才是正确的呢，这就需要我们来验证，我把你们的老朋友也请出来了(方格图)如果1个方格代表1平方米，请你数出它的面积。

 [设计意图：引导学生回顾长方形、正方形面积的计算公式，让学生在已有知识经验的基础上，进而猜测平行四边形面积的计算。]

2.初步验证，感悟方法。

汇报：

生1：我数出来是21平方米。我是先数整格的，再把不是整格的拼成整格的。

生2：我数出来也是21平方米，我是把左边整个三角形平移到右边，拼成长方形后再数的，3×7＝21。

生：只有是沿着高的直角三角形，才可以拼成长方形。

师：为什么就要拼成长方形？

生：拼成长方形好数。

师：把难数的图形转化成容易数的，把平行四边形的面积转化成数长方形的面积。我们把它拼成长方形，这个长方形的面积还是原来平行四边形的面积吗？

生：虽然它被切下来，但是没有缺掉。

生：根本没有变化。

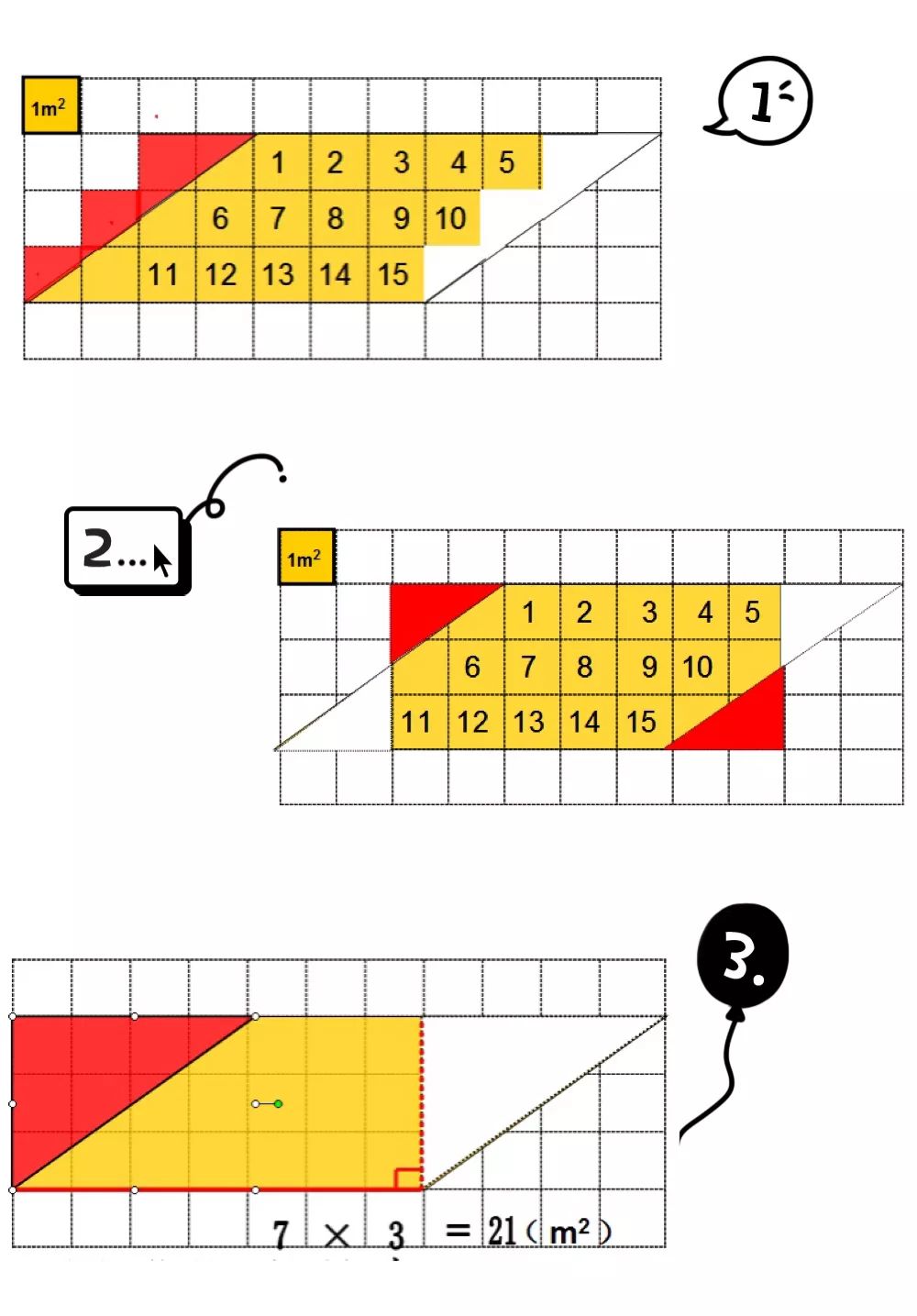
师：它的面积没有多，也没有少，原来转化后长方形的面积就是原来平行四边形的面积。那这个7米是哪条边的长？3米呢？

生：7是长方形的长，又是平行四边形的底。3是长方形的宽，又是平行四边形的高。

师：转化后，这个7和3 具有身份双重。那长方形的面积等于长乘宽，所以平行四边形的面积呢？

生：底乘高。

师：看来，只要把平行四边形转化成长方形，就可以计算出面积了。那是不是所有的平行四边都可以转化成长方形呢？虽然这个图形可以用底乘高去计算，那是不是所有的平行四边形的面积都可以用底乘高来计算呢？仅仅靠数格子一种途径来验证，还不够有说服力。大家想不想自己动手剪一剪，拼一拼？

   [设计意图：让学生在观察、算、数的基础上进行比较，使学生初步领悟到平行四边形和长方形的关系，放手让学生去探索、研究、比较，验证自己的猜想。]

3.  自主探究，推导公式

 1.小组合作，动手操作。

师:是不是所有的平行四边形都可以转化成长方形？

每组学生分得不同的平行四边形，学生动手操作，教师巡视。

2. 剪拼转化，发现规律。

方法1：我们小组是这样剪拼的。我们沿着高剪下一个直角三角形然后平移，拼成长方形。

方法2：也是沿着高剪开，剪下2个三角形，再拼。

方法3：也是沿着高剪开，剪下一个直角梯形。

方法4：沿着另外底边上的高剪

师：大家为什么要沿着高剪呢？

生：因为只有沿着高剪开，才能得到直角，才能拼成长方形。

师：哦，原来沿着高剪开，才是剪拼成长方形的关键。我这样剪可以吗？这样呢？2号图形可以剪拼成长方形吗？怎么剪开？一句话：只要沿着高剪开。3号图形可以吗？老师这里还有1个斜斜的平行四边形，你能把它转化成长方形吗？

生：把它横过来，再沿着高剪开。

师：这个方法可以，如果不旋转呢？就沿着底边上的高剪开呢？

师：看来，再特殊的平行四边形也能转化成长方形。为什么一定要剪拼成长方形？

生：因为长方形面积我们学过。

  [设计意图：把平行四边形转化成长方形，剪、拼的方法是关键。通过剪、拼方法的交流，凸显了剪、拼方法的本质，提升了学生思维的灵活性。动手剪拼，进一步强化了对转化过程的认识和理解，初步感受到底乘高就是面积，为下一步的教学起到了承上启下的作用。]

3. 观察比较，推导公式。

师：原来是用旧知识去解决新问题，把平行四边形转化成长方形那转化后的长方形和原来的平行四边形有什么关系？

生：我发现它们的面积相等。

生：我发现长方形的长就是原来平行四边形的底。

生：我发现长方形的宽就是原来平行四边形的高。

生：因为长方形的面积等于长×宽，所以平行四边形的面积就等于底×高。

师：如果用s表示平行四边形的面积，a表示底，h表示a底边上的高，那么s=ah。

 [设计意图：让学生观察发现转化前、后之间的联系，找共同点，自主推导平行四边形面积的计算公式，表达推导过程，发挥了学生的主体作用，发展了学生抓住关键有序表达的数学能力，有效地突出了教学重点。]

4.  巩固提高，拓展应用

1.计算下面图形的面积。

2.解决问题。

(1)快乐小学要开辟一块形状为平行四边形的植物角，它的面积是12平方米，底是4米，高是多少？你能画出这个平行四边形吗？

(2)在这个植物角的中间开辟一条宽为1米的长方形的小路，你能求出现在绿地的面积是多少吗？

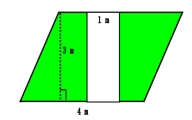
 [设计意图：解决实际问题，增强学生的应用意识。突出对应，明确计算的关键所在。培养学生发现规律、表达想法、阐明道理的能力。]

五、板书设计

想一想

智斗巴依老爷

       巴依老爷家有很大一片菜地，他想找人给菜地翻土地，却又不想给工钱。于是他拿出了4根竹竿，其中2根长7米，两根长5米，对阿凡提说：“阿凡提，我和你打个赌，你用四根竹竿首尾相连去围一块菜地，如果能在一个时辰内把所围成的菜地翻一遍土，我就给你一只羊。否则你除了白白给我翻土以外，还要赔我一只羊。”

       阿凡提说：“好啊！”

       巴依老爷心里盘算着：用这4根竹竿去围成一个长方形地，在一个时辰内是绝对翻不完的，阿凡提肯定输定了。等巴依老爷走后，聪明的阿凡提动手把竹竿调整了一下，在没有改变竹竿4条长度的情况下却让菜地的面积变小了很多。所以，不一会儿，阿凡提就翻完了土，牵走了羊，气得巴依老爷一句话都说不出来。

       你们知道阿凡提是怎么做到的吗？

你若盛开  蝴蝶自来

审核人：郑燕珍    陈金平