深度学习经典网络：ResNet及其变体（ResNet v1）

ResNetv1:https://arxiv.org/abs/1512.03385
pytorch 代码：https://github.com/pytorch/vision/blob/master/torchvision/models/resnet.py
keras 代码：https://github.com/keras-team/keras-applications/blob/master/keras_applications/resnet.py

1 ResNet v1要解决的问题

  深度神经网络朝着网络层数越来越深的方向发展。直觉上我们不难得出结论：增加网络深度后，网络可以进行更加复杂的特征提取，因此更深的模型可以取得更好的结果。但事实并非如此，人们发现随着网络深度的增加，模型精度并不总是提升，并且这个问题显然不是由过拟合（overfitting）造成的，因为网络加深后不仅测试误差变高了，它的训练误差竟然也变高了。作者提出，这可能是因为更深的网络会伴随梯度消失/爆炸问题，从而阻碍网络的收敛。作者将这种加深网络深度但网络性能却下降的现象称为退化问题（degradation problem）。导致网络性能下降的原因是梯度消失问题， 神经网络在反向传播过程中要不断地传播梯度，而当网络层数加深时，梯度在传播过程中会逐渐消失（假如采用Sigmoid函数，对于幅度为1的信号，每向后传递一层，梯度就衰减为原来的0.25，层数越多，衰减越厉害），导致无法对前面网络层的权重进行有效的调整。
  当传统神经网络的层数从20增加为56时，网络的训练误差和测试误差均出现了明显的增长，也就是说，网络的性能随着深度的增加出现了明显的退化。ResNet就是为了解决这种退化问题而诞生的，如图1所示。

图1 20层与56层传统神经网络在CIFAR上的训练误差和测试误差

2 ResNet v1解決退化问题的方案

  一是通过在网络中增加BatchNormalization层, 二是构建恒等映射（Identity mapping), 恒等映射的结构如图2所示.

图 2 ResNet v1残差模块示意图 ResNet-v1的残差单元进行以下的计算：

$$y_l=h(x_l)+\mathcal{F}(x_l,{\mathcal{W}}_l)(1)$$

$$x_{l+1}=f(y_l)(2)$$
这里$x_l$是第$l$个残差单元的输入特征。 W = { W l , k ∣ 1 ≤ k ≤ K } \mathcal{W}=\{ \text{W}_{l,k|1\leq{k}\leq{K}} \} W={ Wl,k∣1≤k≤K​}是一个与第$l$个残差单元相关的权重和偏差的集合，$K$是残差单元内部的层的数量。$\mathcal{F}$是残差函数。函数$f$是元素加和后的操作（ResNet-v1中采用的是ReLU）。函数$h$是恒等映射$h(x_l)=x_l$。
  为什么是恒等映射呢，20层的网络是56层网络的一个子集，56层网络的解空间包含着20层网络的解空间。如果我们将56层网络的最后36层全部短接，这些层进来是什么出来也是什么（也就是做一个恒等映射），那这个56层网络不就等效于20层网络了吗，至少效果不会相比原先的20层网络差吧。同样是56层网络，不引入恒等映射为什么就不行呢？因为梯度消失现象使得网络难以训练，虽然网络的深度加深了，但是实际上无法有效训练网络，训练不充分的网络不但无法提升性能，甚至降低了性能。
  关于残差模块的详细思考将通过以下章节进行介绍。

3 ResNet v1网络结构

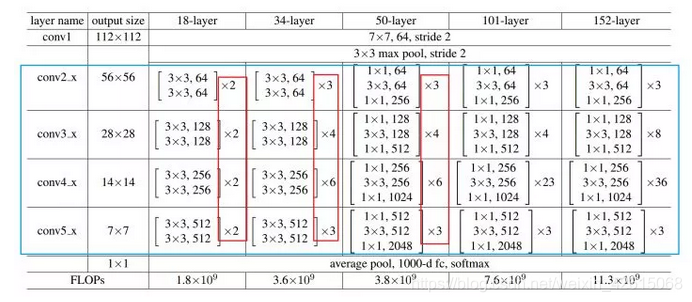
ResNet主要有五种主要形式：Res18，Res34，Res50，Res101，Res152；整体网络结构如图3所示， 残差单元如图4所示， 部分网络片段如图5所示。

图 3 ResNet v1不同网络结构示意图

图 4 不同残差单元示意图

图 5 ResNet v1 局部网络示意图 res18和res34采用图4中左边的残差单元(BasicBlock) ，从res50网上采用右面的残差单元(Bottleneck Block)，整个网络的流程大体分为3步：

• 1数据进入网络后先经过输入部分（conv1, bn1, relu, maxpool）；

• 然后进入中间卷积部分（layer1, layer2, layer3, layer4，这里的layer对应我们之前所说的stage）；

• 最后数据经过一个平均池化和全连接层（avgpool, fc）输出得到结果；

  从layer1-4, 每个层中的第一个残差模块的残差部分采用步长为2的卷积进行下采样，所以在shortcut connection中要采用步长为2的1×1的卷积进行维度的匹配，如图5中的实线部分， 采用的计算方式为H(x)=F(x)+Wx，其中W是卷积操作，用来调整x维度的。剩余其他的残差单元都采用步长为1的卷积，shortcut connection直接连接输入和输出，如图5中虚线部分，采用计算方式为H(x)=F(x)+x。
ResNet v1网络设计规律
整个ResNet不使用dropout，全部使用BN。此外，回到最初的这张细节图，我们不难发现一些规律和特点：

• 受VGG的启发，卷积层主要是3×3卷积；
• 对于相同的输出特征图大小的层，即同一stage，具有相同数量的3x3滤波器;
• 如果特征地图大小减半，滤波器的数量加倍以保持每层的时间复杂度；
• 每个stage通过步长为2的卷积层执行下采样，而却这个下采样只会在每一个stage的第一个卷积完成，有且仅有一次。
• 网络以平均池化层和softmax的1000路全连接层结束，实际上工程上一般用自适应全局平均池化 (Adaptive Global Average Pooling)；

相比传统的分类网络，这里接的是池化，而不是全连接层。池化是不需要参数的，相比于全连接层可以砍去大量的参数。对于一个7x7的特征图，直接池化和改用全连接层相比，可以节省将近50倍的参数，作用有二：一是节省计算资源，二是防止模型过拟合，提升泛化能力；

Bottleneck结构和1×1卷积
ResNet50起，就采用Bottleneck结构，主要是引入1x1卷积。我们来看一下这里的1x1卷积有什么作用：

• 对通道数进行升维和降维（跨通道信息整合），实现了多个特征图的线性组合，同时保持了原有的特征图大小；
• 相比于其他尺寸的卷积核，可以极大地降低运算复杂度；
• 如果使用两个3x3卷积堆叠，只有一个relu，但使用1x1卷积就会有两个relu，引入了更多的非线性映射；

我们来计算一下1*1卷积的计算量优势：首先看上图右边的bottleneck结构，对于256维的输入特征，参数数目：1x1x256x64+3x3x64x64+1x1x64x256=69632，如果同样的输入输出维度但不使用1x1卷积，而使用两个3x3卷积的话，参数数目为(3x3x256x256)x2=1179648。简单计算下就知道了，使用了1x1卷积的bottleneck将计算量简化为原有的5.9%，收益超高。

4 ResNet v1残差单元有效性的理解

从梯度反向传播理解ResNet的有效性
紧接第二部分公式1和公式2， 如果$f$是一个恒等映射：$x_l+1\equiv x_l$，我们可以把公式2带入公式1，得到：
$$x_{l+1}=x_l$$