关于一个非寿险费率厘定例子的学习笔记

最新推荐文章于 2021-08-19 20:18:02 发布

__Lu__

最新推荐文章于 2021-08-19 20:18:02 发布

阅读量5k

点赞数 6

分类专栏：非寿险精算

本文链接：https://blog.csdn.net/weixin_42617297/article/details/104585414

版权

非寿险精算专栏收录该内容

1 篇文章

订阅专栏

关于一个非寿险费率厘定例子的学习笔记

一、计算在当前费率水平下的已赚保费
- 1.1实操
- 1.2 理论补充
二、预测最终赔款与直接理赔费用、最终索赔次数
- 2.1实操
- - 2.1.1 预测最终赔款与直接理赔费用
  - 2.1.2 预测最终索赔次数
- 2.2 理论补充
三、计算索赔强度、索赔频率的趋势因子
- 3.1实操
- 3.2理论补充
- - 3.2.1 赔款数据的调整
  - - 3.2.1.1赔款的趋势调整
四、计算目标赔付率
- 4.1实操
- 4.2理论补充
- - 4.2.1赔付率和其他比率
五、计算总平均费率的调整幅度
- 5.1实操
- 5.2理论补充
六、计算各个风险类别的趋势化最终赔款
- 6.1 实操
七、计算各个风险类别的平均相对费率
- 7.1 实操
八、计算各个风险类别的加权平均相对费率
- 8.1 实操
- - 8.1.1 计算驾驶员类型的加权平均相对费率
  - 8.1.2 计算行驶区域的加权平均相对费率
九、进行平衡调整
- 9.1 实操
十、计算各个风险类别的新费率
- 10.1 实操
十一、计算赔偿限额为100/300的増限因子
- 11.1 实操
十二、新费率表
- 12.1 实操
- 12.2 理论补充
- - 12.2.1 费率厘定的基本原则
附录
- 1.Python代码实操
参考

       下面将通过一个私人汽车人身伤害保险的例子来说明费率厘定的主要步骤。需要说明的是，该例的数据是假设数据。
       本例采用单项分析的方法计算相对费率，但在实务中更多地采用广义线性模型。
       假设该险种的当前费率如表1和表2所示，该费率于2006年7月1日生效，该费率表中包括两个费率因子，即行驶区域和驾驶员类型，分别包含三个水平。基本赔偿限额是每人2万元，每次事故4万元，表示为20/40。行驶区域2、驾驶员类型1为基础风险类别，费率为80。该费率表中还包括一个増限因子，用来计算赔偿限额从基本限额增长到100/300时的费率。下面讨论如何厘定该险种在2008年7月1日开始生效的新费率。

表1 私人汽车人身伤害保险基本赔偿限额（20/40）的当前费率（2006年7月1日）
行驶区域	驾驶员类型1	驾驶员类型2	驾驶员类型3
行驶区域	成年驾驶，无年轻驾驶者	家庭中有年轻驾驶者，但不是主要驾驶者	年轻的车主或主要驾驶者
1.中心城市	140	182	252
2.郊区	80	104	144
3.其他地区	60	78	108

表2 100/300赔偿限额的増限因子
赔偿限额	増限因子
100/300	1.3

完成上述费率厘定过程需要的数据如下：

       1.2002年到2007年分行驶区域和驾驶员类型的已赚风险单位数
       2.2002年到2007年的已发生赔款数据，排列成流量三角形的形式
       3.2002年到2007年的索赔次数数据，排列成流量三角形的形式
       4.该险种的费用率、利润率，用于计算目标赔付率
       5.2005年到2007年分行驶区域和驾驶员类型的已发生赔款数据，用于计算分类费率
       6.无赔款限额、基本赔款限额和增长限额三种情况下赔款金额和索赔次数的分布，用于计算赔款限额为100/300时的増限因子

一、计算在当前费率水平下的已赚保费

1.1实操

本例的经验期是2005-2007年3年。3年中，各类别与各区域的已赚风险单位数如表3所示。
用风险单位数扩展法计算在当前费率水平下的已赚保费，就得到各类别和各区域在当前费率水平下的已赚保费，如表4所示。
在这里插入图片描述

1.2 理论补充

1.2.1 风险基础和风险单位

       当保单持有人将其潜在损失转移给保险人时，保险人需要收取保险费。保险费应该与保单持有人的潜在损失成比例。而度量潜在损失大小的一个基本工具就是风险基础，它近似量化了风险的大小。此，风险基础也就是保费基础，它的大小决定着保费的高低。
       最常用的风险单位数统计量有承保风险单位数(written exposures)、到期风险单位数(earned exposures)、未到期风险单位数（unearned exposures）和有效风险单位数(in-forceexposures)。承保风险单位数是指在一定时期内保险人已经签订了保险合同的风险单位数。到期风险单位数是指在一定时期内保险人已经提供了相应的保险保障的风险单位数。未到期风险单位数是指在承保的风险单位数中，截至某个时点，保险公司尚未提供保险保障的风险单位数。有效风险单位数是指在某一时点上保险人正在承担保险责任的风险单位数。需要注意的是，承保风险单位数、到期风险单位数和未到期风险单位数都是时期指标，而有效风险单位数则是一个时点指标。
       从理论上讲，一个好的风险基础应该满足下述三个条件：
       （1）风险基础应该是对潜在损失的准确度量，这样才能确保费率厘定结果的准确性。
       （2）风险基础应该便于保险人实际使用和核实，否则无法用于费率厘定。
       （3）风险基础应该不易受到人为操纵。
       保费不仅与风险基础有关，而且与费率因子有关。风险基础与期望损失（纯保费）是一致的、连续的乘法关系，而费率因子与期望损失是离散的、非线性的关系。
       在许多险种中，影响被保险人潜在损失的因素是很多的，但并非所有的影响因素都可以在费率厘定中得到应用，其中主要的原因是：
       （1）某些影响因素难以确定，过于主观，或波动很大。
       （2）不被社会所接受，如种族和宗教，即使损失数据可以证明它们与索赔频率有关，保险公司也不会使用这类变量厘定保险费率。
       在影响期望损失的所有可以使用和量化的因素中，与期望损失最具有一致性关系的因素可以确定为风险基础，而其他因素则可以作为费率因子使用。
       在各种保险业务中，影响期望损失的因素很多，但只有一个可以作为风险基础使用。

1.2.2 保费及其构成

       保费（premium）是投保人购买保险产品时向保险人所支付的价格，由纯保费和附加保费构成。纯保费用于支付保险公司在未来的期望赔款，而附加保费用于支付保险人的各种费用并给保险人提供承保利润附加。保险费率（premium rate）简称费率，是指每一个风险单位的保费。
       纯费率（pure premium rate）是指保险公司对每一风险单位的平均赔款金额，通常用赔款总额与风险单位数之比进行估计
       纯费率就是索赔频率与索赔强度的乘积。 $P=\frac{N}{E}·\frac{L}{N}$
       与风险单位数的统计量类似，在保费的统计中，也区分承保保费（written premium）、已赚保费（earned premium）、未赚保费（unearned premium）和有效保费（in-force premium）。承保保费是指保险人在一定时期内因承保业务而收取的保险费。已赚保费也被称作满期保费，是指在保险人所收保费中，已尽保险责任所对应的那部分保费。未赚保费也被称作未到期保费，是指在保险人所收保费中，未尽保险责任所对应的那部分保费。有效保费是指在某个时点上全部有效保单在整个保险期间的保费之和。
       总保费与总的风险单位数之比就是总平均保费，它可以反映业务构成的变化，譬如，当高风险的业务所占比重增加时，总平均保费就会上升。费率厘定的通常方法是首先确定总平均保费，然后通过各种费率因子对总平均保费进行调整得到各个风险类别的保费。厘定总平均保费的方法主要有纯保费法和赔付率法。
       除了补偿保险公司支付的赔款和费用外，保费中还应该包含合理的利润附加。利润附加可以看作是对保险公司承担风险的补偿，因此其大小与保险公司承担的风险水平有关，传统上通常将其表示为保费的一定百分比。
       保险方程： $保费 = 赔款 + 理赔费用 + 承保费用 + 利润附加$
       保险定价的目标就是要使保险方程达到平衡，即保险公司收取的保费应该足以补偿其预期的赔款和费用支出，同时可以实现保险公司的承保利润目标。
       费率厘定过程是一种前瞻性预测，因此在应用经验数据对当前费率的充足性进行评价时，应该考虑到许多因素都会影响保险方程右边的各个项目，如经验期的费率变化、经营管理水平的变化、业务构成的变化、有关法律法规的变化和通货膨胀等，都有可能对赔款和费用等造成影响。因此，在应用经验数据厘定保险费率时，必须对这些数据进行适当的调整，即将它们都调整到未来新费率的生效时期。
       在对当前的费率进行充足性评价时，还需注意上述保险方程应该在两个层次上达到平衡，即总体水平上的平衡和个体水平上的平衡。所谓总体水平上的平衡是指保险公司收取的总保费应该足以支付其赔款和费用，并实现公司的总体目标利润。如果当前的费率水平不能实现保险公司的目标利润，或者实际利润超过了目标利润水平，就应该提高或降低当前的总平均费率水平。所谓在个体水平上的平衡是指对于不同的个体风险或不同类别的风险，它们的保费应该与其风险水平成比例，风险越高，保费也应该越高。

1.2.3 数据的汇总方法

       在风险单位、保费和赔款等数据的汇总中，有以下四种方式可以选择使用，即事故年度法、保单年度法、日历年度法和报案年度法。
       （1）按事故年汇总数据
       这是汇总精算数据最常见的方法。按事故年汇总数据就是以事故发生为统计标准，把发生在同一个日历年度的保险事故所对应的赔款和保费等数据汇总在一起。相应地，如果这个日历年是 2008 年，则该事故年就被称作 2008 事故年。
       按照事故年汇总赔款数据，由于报案延迟和理赔延迟的影响，在每个事故年结束之后，不能马上得到准确的赔款统计数据，而只能进行估计，即需要对未决赔款准备金进行估计，然后将其与已付赔款相加，得到最终赔款的估计值。随着时间的推移，未决赔款都会逐渐转化为已付赔款。
       按事故年汇总数据的优点是，所有赔案发生在同一年，具有近似相同的风险环境，因此赔款数据的统计稳定性相对较好。此外，按照事故年汇总赔款和保费数据，可以较好地体现赔款与保费之间的配比关系。
       （2）按保单年汇总数据
       按保单年汇总数据就是以保单生效日期为统计标准，把在同一个日历年度生效的保单所对应的赔款和保费等数据归集在一起。相应地，如果这个日历年是 2008 年，则该保单年就被称作 2008 保单年。
       在每个保单年度末，统计数据都是不完整的，因为很多保单都还没有到期。这可能是按保单年汇总数据的最大缺陷。
       如果按保单年汇总数据，在每个保单年度末的赔款数据就是已付赔款与未决赔款准备金之和，其中未决赔款准备金是该保单年所承保的保单已经发生和将要发生的所有赔款。
       按保单年汇总保费和赔款数据的优点是能够完全体现保费和赔款之间的配比关系，因为它们都对应着相同年度承保的业务。
       （3）按日历年汇总数据
       按日历年汇总数据就是把发生在同一日历年度的会计数据归集在一起，而不论事故的发生年度和保单的生效年度。
       日历年度的已付赔款（paid loss）就是在该日历年实际支付的赔款，而不论事故的发生日期和保单的生效日期。日历年的已报案赔款（reported loss）是已付赔款和逐案估损准备金的提转差，即： $日历年 X 的已报案赔款 = 日历年 X 的已付赔款 + 日历年 X 的逐案估损准备金 - 日历年（ X - 1 ）的逐案估损准备金$
       可见，日历年的已报案赔款既不与特定的事故年对应，也不与特定的保单年对应。在每个日历年度末，就可以完全确定该日历年的已报案赔款，这是按日历年汇总数据的优点之一。按日历年度汇总保费和赔款数据的缺点是不能很好地体现它们之间的配比关系，因为日历年度的已赚保费来自于当年的有效保单，这些保单可能是当年承保的，也可能是去年承保的，而日历年度的赔款却有可能来自于多年前承保的保单。
       按日历年度汇总的数据可以用于报案延迟和理赔延迟都很短的保险业务的费率厘定。
       （4）按报案年汇总数据
       按报案年汇总数据就是以保险事故的报案时间为统计标准，把在同一个日历年度报案的赔款数据归集在一起，而不考虑事故的发生日期和保单的生效日期。相应地，如果这个日历年是 2008 年，则该报案年就被称作 2008 报案年。
       按报案年度汇总的数据主要用于索赔报案制保单（claims-madepolicy）的定价。
       在实际应用中，数据的汇总方法取决于费率厘定的需要。譬如，如果只需对某个产品的总体费率水平进行充足性评价，则可以根据上述方法按年度（如保单年、事故年、日历年或报案年）汇总风险、保费和赔款数据。但是，如果需要厘定分类费率，则最好使用个体保单的数据，或者根据选用的费率因子对数据按年度进行交叉汇总。

1.2.4 风险单位数与保费数据的汇总

       用风险单位数乘以相应的费率就可以得到保费，所以保费数据的汇总方法与风险单位数的汇总方法完全相同。下面仅讨论风险单位数的汇总方法。
       数据的汇总方法有四种，即日历年度法、事故年度法、保单年度法和报案年度法，但是在汇总风险单位数时，只有日历年度法和保单年度法可以使用，而事故年度法与日历年度法对风险单位数的汇总结果通常相同（个别情况例外），所以暂不讨论应用事故年度法对风险单位数的汇总。
       下面还是通过一个简化了的例子来说明风险单位数的汇总方法，假设每份保单只承保一个风险单位，且保单期限均为 1 年。3 份保单的有关信息如下表所示：
在这里插入图片描述
       上表中的保单可以通过下图进行描述。在该图中，横轴表示时间，纵轴表示保单期限结束的百分比。每一条斜线代表一份保单。譬如，保单 A 由第一条斜线表示，该保单在2011 年 10 月 1 日生效，在生效日当天，保单期限结束的比例为零，所以斜线的起始点对应于纵轴的 0%位置。在 2012 年 10 月 1 日，保单 A 到期，保单期限完全结束，所以在到期日，斜线的终点对应于纵轴的 100%位置。
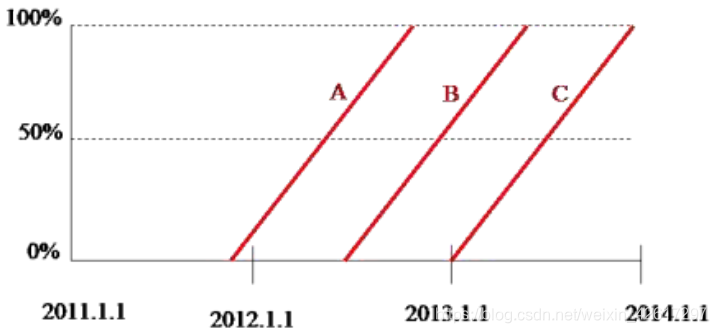
在这里插入图片描述
       如前所述，在对风险单位数进行汇总时，可以采用日历年度法或保单年度法，而风险单位数又有承保风险单位数、到期风险单位数、到期风险单位数和有效风险单位数之分，下面分别讨论这些风险单位数的汇总方法。
       （1）承保风险单位数
       如果按日历年度汇总承保风险单位数，则容易看出，保单 A 的承保日期在 2011 年，保单 B 的承保日期在 2012 年，而保单 C 的承保日期在 2013年，所以这三年各有一个承保风险单位数（如下图所示）。注意，在本例中，每份保单只对一个日历年度的承保风险单位数有贡献。但是，如果一份保单在中途撤销，则该保单就有可能对两个日历年度的承保风险单位数有贡献。譬如，假设保单 B 在 2013 年 4 月 1 日退保，此时该保单的期限已经完成了 75%，剩余 25%没有完成。在这种情况下，保单 B 在 2012 日历年的承保风险单位数仍然等于 1，但在 2013 日历年的承保风险单位数应该为负值，即为-0.25。
在这里插入图片描述
       如果按保单年度汇总承保风险单位数，则容易看出，2011 保单年、2012 保单年和 2013 保单年的承保风险单位数都为 1，分别对应于保单 A、B 和 C（如图 1 1- -4 4 所示）。与日历年不同的是，即使有中途退保的保单，每份保单也只对一个保单年的承保风险单位数有所贡献。譬如，假设保单 B 在 2013 年 4 月 1 日退保，此时该保单的期限已经完成了 75%，所以它在 2012 保单年的承保风险单位数就变为 0.75。
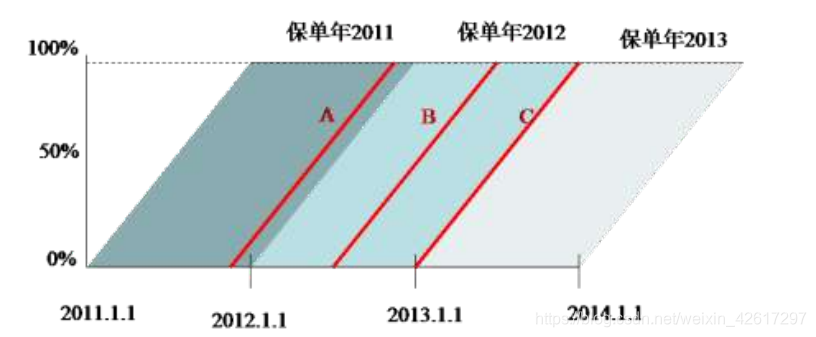
在这里插入图片描述
       （2）到期风险单位数
       到期风险单位数是指在承保风险单位数中已经到期的风险单位数。譬如，保单 A 是在 2011 年 10 月 1 日承保的，期限是 1年，所以在2011年到期的风险单位数为3/12=0.25，在2012年到期的风险单位数为9/12=0.75。保单 B 是在 2012 年 7 月 1 日承保的，保险期限为 1 年，所以在 2012 日历年和 2013 日历年到期的风险单位数各占一半，均为 0.5。保单 C 是在 2013 年年初承保的，在当年年末到期，所以保单 C 为 2013 年贡献了 1 个到期风险单位数。由此可见，对于本例中的三份保单，2011日历年的到期风险单位数为 0.25，2012 日历年的到期风险单位数为 0.75+0.5=1.25，2013 日历年的到期风险单位数为 0.5+1=1.5。
       保单年的到期风险单位数，每份保单的到期风险单位数都归集在该保单的承保年度，而且随着时间的推移成比例地增加。譬如，在上例中，对于 2012 保单年，只有保单 B 属于该保单年度，所以截至 2013 年 1 月 1 日的到期风险单位数为 0.5，而截至 2013 年 7 月 1 日的到期风险单位数为 1。当保单年度结束以后（对于一年期保单，如果从保单年度的起始点计算，24 个月以后，保单年度才能结束），保单年的到期风险单位数就等于其承保风险单位数。
       （3）未到期风险单位数
       日历年或保单年的未到期风险单位数等于承保风险单位数减去到期风险单位数。
       （4）有效风险单位数
       有效风险单位数是在某个时点上有可能发生保险事故从而可以提出索赔的风险单位数。譬如，2011 年 10 月 20 日的有效风险单位数就是在该日承保或在该日之前承保并且在该日之后仍然有效的保单所包含的所有风险单位数之和。譬如在上例中，2012 年 8 月 1 日的有效风险单位数为 2，分别来自保单 A 和保单 B，就是下图中经过 2012 年 8 月 1 日的一条竖线穿过的两份保单。
在这里插入图片描述
       对于其他期限的保单，风险单位数的汇总方法与一年期保单类似，此处不再赘述。
       前面的讨论都是对个体保单数据的汇总，但在有些情况下，可能需要对汇总后的风险单位数进一步汇总，譬如我们已经有了各个月份的承保风险单位数，现在需要计算各个月份的到期风险单位数。对于这类数据的汇总，通常假设所有保单的承保日期都发生在各个期间的中点，譬如对于月度数据，假设所有保单的承保日期都是在每月的 15 日。这种方法正好将一年划分成了 24 个区间，所以通常将这种方法称作 24 法则。下面通过一个简例说明 24法则的应用。
       假设 2011 年各个月份承保的风险单位数均为 240，则有效风险单位数和到期风险单位数的计算过程如下表所示。注意，在有效风险单位数的统计中，因为假设 7 月份的保单都是在该月 15 日承保的，所以该月在 7 月 1 日的有效风险单位数为零。
在这里插入图片描述

1.2.5 保费数据的调整

对保费数据的调整主要包括两方面，即水平调整和趋势调整。水平调整是指把经验期的保费按照当前的费率水平重新进行计算。趋势调整是指把当前的费率水平调整到未来新费率的使用期。

1.2.5.1 保费的水平调整

       通常而言，如果经验期包括若干年，则各年的费率水平很可能不同。此时，如果应用赔付率法厘定保险费率，就需要将经验期的费率都调整到当前的费率水平，并在此基础上计算已赚保费，即得到当前费率水平下的已赚保费。计算当前费率水平下已赚保费最精确的方法是将经验期的每一份保单都按照当前的费率水平重新计算保费，这种方法被称作风险单位数扩展法（extension of exposures），但这种方法要求已知详细的风险单位数数据，且计算的工作量相对较大。作为这种方法的一种替代，可以使用平行四边形方法进行近似估计。平行四边形方法假设风险单位数在经验期内是均匀分布的，并根据简单的几何关系，可以将经验期的已赚保费调整到当前的费率水平。下面通过一个简例说明调整过程。
       假设经验期包括 2001 年、2002 年和 2003 年，每份保单的保险期限均为 12 个月，过去几年的费率调整情况如下表所示。
在这里插入图片描述
       如果把 1999 年 7 月 1 日的相对费率水平确定为 1，则 2000 年 7 月 1 日的相对费率水平为 1.12，而 2002 年 7 月 1 日的相对费率水平为 1.12×1.1 = 1.232。
       由于所有保单的保险期限均为 12 个月，所以在经验期的第一年（2001 年），已赚保费要么是按相对费率水平 1 承保的（如在 2000 年上半年承保的保单），要么是按相对费率水平1.12 承保的（如在 2000 年下半年或 2001 年承保的保单）。
       下图是关于上述数据的平行四边形表示法，其中横轴表示保单的生效日期，纵轴表示保单期限结束的百分比。实线将图形分割成了三个部分：第一部分的相对费率水平为 1，第二个部分的相对费率水平为 1.12，第三个部分的相对费率水平为 1.232。
       可以看出，2001 日历年度的已赚保费由两部分构成：一部分（左上三角形）是按相对费率 1 计算的，而其他部分是按相对费率 1.12 计算的。2002 日历年度的已赚保费也由两部分构成：一部分（右下三角形）是按相对费率 1.232 计算的，而其他部分是按相对费率 1.12 计算的。同样的道理，2003 日历年度的已赚保费也由两部分构成：一部分（左上三角形）是按相对费率 1.12 计算的，而其他部分是按相对费率 1.232 计算的。
在这里插入图片描述
       下面以 2001 日历年度为例，说明如何将该年的已赚保费调整为按当前费率水平表示的已赚保费。下图是 2001 年已赚保费的构成情况。

       如果假设保险公司在 2001 年承保的业务是均匀分布的，则从上图可以看出，在 2001年的已赚保费中，有 12.5%的已赚保费（用左上三角形表示，面积为 0.5×0.5÷2＝0.125）是按相对费率 1 计算的，另外 87.5%是按相对费率 1.12 计算的。因此 2001 年的平均相对费率水平为1×12.5% + 1.12×87.5% ＝ 1.105
       由于当前的相对费率水平为 1.232，因此将 2001 年的已赚保费乘以下述系数即得 2001年的已赚保费按当前费率计算的已赚保费：1.232÷1.105 ＝ 1.1149
       上述系数被称作当前费率水平因子。应用当前费率水平因子乘以 2001 年的已赚保费，即得 2001 年的当前费率水平下的已赚保费。
       对 2002 年和 2003 年的已赚保费作同样的调整，即可得到整个经验期的在当前费率水平下的已赚保费（参见下表）。
在这里插入图片描述
       将三个日历年度在当前费率水平下的已赚保费相加，即得整个经验期在当前费率水平下的已赚保费为 4376.1 万。
       需要特别注意的是，应用平行四边形方法的一个重要假设是保险公司承保的保单在经验期内均匀分布，如果实际情况并非如此，如每年的某些季度承保的保单较多，而其他季度承保的保单较少，则用这种方法计算经验期在当前费率水平下的已赚保费会产生较大的误差。一种解决办法是按季度应用平行四边形方法，即假设保险公司在每个季度承保的业务是均匀分布的。

1.2.5.2 保费的趋势调整

类似于赔款和费用会受到通货膨胀等经济因素的影响而不断变化，每个风险单位的平均保费也存在趋势变化。事实上，即使在费率保持不变的情况下，每个风险单位的平均保费也可能随着时间而有显著的变化。譬如，如果业务组合中高费率的保单所占比例增加，每份保单的平均保费水平也会上升。Jones（2002）在“introduction to premium trend”一文中较为全面地讨论了保费的趋势调整问题，下面就是对其主要内容的简要介绍。

1.2.5.2.1. 平均保费水平的影响因素

       造成未来平均保费水平和历史平均保费水平不同的因素主要包括：费率在经验期的变化；费率厘定系统的变化；费率厘定系统对平均保费水平的影响；业务结构的变化。
       这些变化对平均保费水平所产生的影响不尽相同：既可能是一次性的影响，也可能是持续性的影响；既可能是可测量的影响，也可能是无法测量的影响；既可能是突发的影响，也可能是渐进的影响。
       下面分别讨论上述每一种因素对平均保费水平所产生的影响：
       （1）费率在经验期的变化
       费率在经验期发生的变化对平均保费水平产生的影响是一次性的、也是可测量的。在费率厘定时，通常需要把经验期的保费都调整到当前的费率水平上。
       （2）费率厘定系统的变化
       费率厘定系统的变化主要包括采用了新的费率厘定系统，或对已有的费率厘定系统进行调整。这些变化通常对平均保费水平会产生一次性的、可测量的影响。费率厘定系统的变化可以分为两种类型：一种是费率的变化(Rate Level Changes)。譬如，如果费率系统对某种风险提供 5％的折扣，而将近一半的保单持有人符合折扣条件，那么总的保费水平将大约下降2.5％，这与基准费率下降2.5％的效果是相同的。另一种是保费的变化(Premium Level Changes)。譬如，在汽车保险中，如果将责任限额从 15 万元上调到 20 万元，那么保单持有人将会支付更高的保费，当然也会获得更多的保障。
       上述两种类型的变化对未来的保费水平会产生直接影响，其中第一种类型的变化只会影响保费的大小，而第二种类型的变化会同时影响保费和赔款的大小。
       （3）费率厘定系统本身对平均保费水平的影响
       很多公司采用的费率厘定系统本身会对平均保费水平不断产生影响。这种影响通常是可测量的、连续的、渐进的，而且预计在未来的保险期间仍将持续。譬如，在车损险中，模型年计划(model year plan)和车辆标志计划(vehicle symbol plan)将对汽车保险的平均保费水平产生持续向上的推力。
       模型年计划赋予较新生产的汽车较高的费率因子，目的是为了考虑不断增加的修理和重置费用。随着保单持有人淘汰旧车，购买新车，模型年费率因子会不断提高，因而保单持有人所缴纳的保费也会随之上升。这种费率厘定系统产生了一种自动上调保费的趋势，因此降低了汽车保险费率上调的需求。事实上，如果汽车保险的赔款增长幅度低于保费的增加幅度，还需要对费率水平进行适当的下调。
       类似于模型年计划，车辆标志计划也将产生保费上升的趋势。车辆标志因子从直观上看是基于新车价格的，越是昂贵的汽车，其费率因子也越高，所以随着保单持有人以更昂贵的新车替换掉旧车，车辆标志因子的平均水平也会不断上升。
       许多公司同时采用模型年计划和车辆标志计划，在这种情形下，两种计划叠加会产生更为显著的保费上升趋势。
       （4）业务结构的变化
       在某些情况下，业务结构的变化可能是突发的，譬如刚刚接受了另外一家保险公司的某种业务。然而，对于大多数公司而言，业务结构的变化通常是连续的、渐进的。
       业务结构的变化对平均保费水平会产生显著影响。譬如，如果被保险人选择更高的免赔额以降低保费，就会造成下降的保费趋势；如果保险公司承保了更多的高风险业务，就会造成上升的保费趋势。
       由于业务结构的变化，即使将经验期的保费已经调整到了当前的费率水平，经验期的平均保费水平仍然有可能不同于当前的平均保费水平，因此有必要对当前费率水平下的历史保费再次进行调整，以反映未来保险期间可能出现的业务结构的变化。需要注意的是，在进行这一调整时，必须明确经验期的业务结构变化是否在未来有可能继续发生。

1.2.5.2.2. 调整方法

       有两种方法可以对影响平均保费水平的各种因素进行调整。
       一种方法是根据当前的情形，重新计算经验期的保费。从理论上讲，这种调整是精确的，适用于一次性和可测量的影响，其隐含的假设是，经验期发生的变化在未来不会持续，因此对平均保费水平的影响已经停止，譬如费率在经验期发生的变化就是这种情况，它对平均保费水平的影响是一次性的，也是可以测量的。
       另一种方法是观察经验期内平均保费水平的总体变化趋势，选定年平均趋势因子，并将其应用于经验期的保费。根据年平均趋势因子，可以将经验期内每一年的平均保费水平都调整到未来保险期间的平均保费水平。当经验期发生的某些变化对平均保费水平的影响是连续的并且难以精确测量时，通常会采用这种方法。这种方法假定，经验期发生的变化在未来还会持续。譬如，业务结构逐渐向更高责任限额的变化不仅会造成经验期平均保费水平的上升，而且这种变化在未来的保险期间仍会持续。
       需要注意的是，在对经验期的保费进行调整时，只可采用其中的一种方法，否则就会重复计算这些变化对平均保费水平所产生的影响。因此，如果选择了第一种方法对影响平均保费水平的变化进行了调整，那么在分析保费趋势时必须确保没有对这一变化进行重复计算。
       如果经验期的变化对平均保费水平的影响是一次性的、突发的和可测量的，可以应用第一种方法对经验期的保费直接进行调整；如果经验期的变化对平均保费水平的影响是连续的、渐进的并且难以测量，则可以通过观察经验期平均保费水平的变化趋势对经验期的保费进行调整，即应用第二种方法。
       为了更加直观地说明重复计算带来的影响，下表给出了一组假设的承保保费数据。下图显示了最近 24 个季度的 12 月移动平均承保保费。注意，从第 12 季度到第 16 季度之间，平均承保保费出现了快速上升，这是由于在经验期的中点费率上调了 25%所致（参见下表）。
       如果不剔除费率在经验期的一次性变化（上升），应用指数回归可以得到年平均保费的趋势增长因子，相应的指数回归方程可以表示为： $y=a×b^t$ ，其中 $y$ 表示 12 月移动平均承保保费， $t$ 表示时间（季度）。注意，在建立回归方程时，第一个移动平均承保保费对应的时间为 $t = 1$
       上式两边取对数，可以将其转化为线性回归方程： $l n y = l n a + t l n b$
       应用下表中第（9）栏的数据，容易得到下述回归结果： $l n 5.9352 \to a = 378.13, l n b = 0.02313, b = 1.0234$
       由此可见，如果不剔除费率在经验期的一次性变化，每个季度的平均保费增长率大约为2.34%，相应的年平均保费增长率大约为 9.7%。
       应用相同的回归方法，如果剔除费率在经验期一次性上升的影响，即应用下表中第（10）栏的数据，在当前费率水平下计算年平均承保保费的趋势增长因子，大约为 3%。
       因此，对于本例的数据，恰当的方法是首先对费率的一次性变化进行调整，然后用调整后的数据拟合平均保费水平的增长趋势因子。换言之，在本例中，只有 3%的年趋势增长因子在未来是有可能持续的。如果用 9.7%预测未来的保费增长趋势，显然会严重高估未来的平均保费水平。
在这里插入图片描述
       下表给出了上图所使用的各种数据。该表中 12 个月移动平均承保保费和在当前费率水平下的平均承保保费是每个风险单位的保费。该表中的“移动总和”是指 12 个月（4 个季度）移动总和，譬如第（5）栏“承保保费”的移动总和就是相邻 4 个季度的承保保费之和，譬如，第一个值是 1-4 季度的承保保费之和，即 1667138 = 400000+411033+422198+433907，第二个值是 2-5 季度的承保保费之和，即 1712922 = 411033+422198+433907+445784。
在这里插入图片描述

       如前所述，影响平均保费水平的因素主要包括四种类型，下面分别给出相应的调整方法。
       （1）费率在经验期的变化
       费率在经验期发生的变化对平均保费水平产生的影响是一次性的、可测量的，因此可以将经验期的保费直接调整到当前的费率水平。
       （2）费率厘定系统的变化
       费率厘定系统的变化对平均保费水平所产生的影响也是一次性的、可测量的，因此可以将经验期的保费直接调整到当前的费率水平。
       在分析平均保费水平的变化趋势时，必须剔除已经经过直接调整的前述两种影响因素
       （3）费率厘定系统本身对平均保费水平的影响
       保险公司使用的一些费率厘定系统本身也会造成平均保费水平的不断变化，这种费率厘定系统对平均保费水平产生的影响是可测量、连续的、渐进的。如前所述，选择调整方法的关键是首先要判断影响平均保费水平的变化因素在未来的保险期间是否会延续。如果这种变化会继续保持，可以将这种变化引入趋势因子中进行调整；如果这种变化预计不再延续，可以对这种变化进行直接调整。
       （4）业务结构的变化
       业务结构的变化对平均保费水平的影响类似于费率厘定系统。因此在调整前，首先需要明确业务结构的变化在未来的保险期间是否会延续，如果这一变化已经停止，可以直接调整；如果这一变化会延续，可以将这种变化引入趋势因子中进行调整。如果在每一个费率因子下都有完整的风险单位数数据，就可以直接调整。譬如，假设在经验期投保人的男女性别比例为 6：4，他们的费率因子分别为 1.2 和 1，平均费率因子为 1.12。预计在未来的保险期间，投保人的性别比例为 5：5，费率因子保持不变，平均费率因子为 1.1。在这种假设下，容易求得平均保费水平将下降 1.79%。

1.2.5.2.3 趋势期限和趋势因子

       用 12 个月移动平均保费序列计算保费增长趋势不会受到风险单位数变化的影响，还可以平滑掉可能存在的随机波动。与赔款的增长趋势不同，对于大多数险种而言，平均保费水平的增长趋势没有显著的季节效应。
       由于保费有承保保费和已赚保费之分，那么在分析平均保费水平的增长趋势时，应该使用平均已赚保费序列还是平均承保保费序列呢？对于这个问题有两种不同的观点。
       一种观点认为，最终的保费趋势因子将应用于经验期在当前费率水平下的已赚保费，所以应该用平均已赚保费序列进行趋势分析。
       另一种观点认为，虽然经验期的保费是已赚保费，但是可以确定经验期已赚保费的平均承保日期，进而分析平均承保保费的变化趋势，因此基于平均承保保费的保费趋势分析方法也是有效的。此外，与平均已赚保费相比，平均承保保费包含的信息更加靠近新费率的使用期，从而可以更好地反映业务结构的最新变化。这是因为，对于任意一份保单而言，只有承保以后，承保保费才会逐渐转变为已赚保费。
       确定平均保费水平的变化趋势主要有两种方法，即一步法和两步法。
       一步法在整个经验期和未来的保险期间都采用单一的年度趋势增长因子，并且分别对经验期内每一年的保费进行单独的趋势调整，但都要趋势化至同一个时点。这种方法为大多数公司所采用，并且也是对赔款进行趋势化调整的标准方法。下图以 2001 日历年为例，说明了保费的趋势调整和趋势期限的选择。
       因为对保费趋势进行分析的基础是平均承保保费，所以经验期内每一年合理的趋势期限应该是从该年的平均承保日期到未来保险期间的平均承保日期。需要注意的是，经验期内每一日历年的中点为该日历年保费的平均已赚日期，平均承保日期要比平均已赚日期提前半个保险期间。对于保险期间为 12 个月的保单而言，平均承保日期要比平均已赚日期提前半年。
       下面以下图中 2001 事故年为例说明如何确定趋势期限。假设所有保单的保险期间为 12 个月，经验期为 2000—2002 年，新费率生效日期为 2004 年 1 月 1 日。2001 年的第一笔已赚保费来自 2000 年 1 月 2 日承保的保单，因为这些保单有效期的最后一天为 2001 年 1月 1 日；2001 年的最后一笔已赚保费来自 2001 年 12 月 31 日承保的保单。由此可见， 2001年的已赚保费对应的承保区间为 24 个月。由于对称效应（例如 2000 年 1 月 1 日承保的保单对日历年 2001 年已赚保费所做的贡献和 2001 年 12 月 31 日承保的保单对 2001 年已赚保费所做的贡献是相等的；2000 年 1 月 2 日承保的保单对 2001 年已赚保费所做的贡献和 2001年 12 月 30 日承保的保单对 2001 年已赚保费所做的贡献是相等的），2001 年已赚保费对应的平均承保日期为这 24 个月的中点，也就是 2001 年 1 月 1 日，比 2001 年已赚保费对应的平均已赚日期 2001 年 7 月 1 日提前了半个保险期间，即 6 个月。由此可见，对 2001 年已赚保费进行调整的趋势期限为 3.5 年。类似地，对 2000 年和 2002 年的已赚保费进行调整的趋势期限分别为 4.5 年和 2.5 年。
在这里插入图片描述
       另一种对保费进行趋势调整的方法是 两步法，可以看做是对一步法的改进。之所以使用两步法，是因为对经验期的每一年使用统一的年度趋势因子也许是不合适的，例如下图中所展示的情况。
       该图表明，在当前的费率水平下，平均承保保费在观测期的中间有所下降，随后又上升到初始水平。假设在未来的保险期间，平均保费水平每年增长 5％。如果采用一步法确定趋势因子，就必须把经验期的趋势因子（在下图中大约为 0％）和未来保险期间的趋势因子（5%）进行折中处理，通常会选择这二者的某种平均值，如 2％。但这种方法存在的问题是，如果第一年处于经验期之内，则将第一年的保费趋势化至未来保险期间的总趋势因子应该与第六年的总趋势因子相等，因为该图表明它们的平均保费水平相等。但是，如果采用一步法，将使得第一年比第六年多出 5 年的趋势期限，从而导致第一年的总趋势因子要远远大于第六年。此外，将第三年的保费趋势化至未来保险期间的总趋势因子应该大于第一年和第六年，因为该图表明第三年的平均承保保费低于第一年和第六年，但在一步法中显然无法实现这一点。
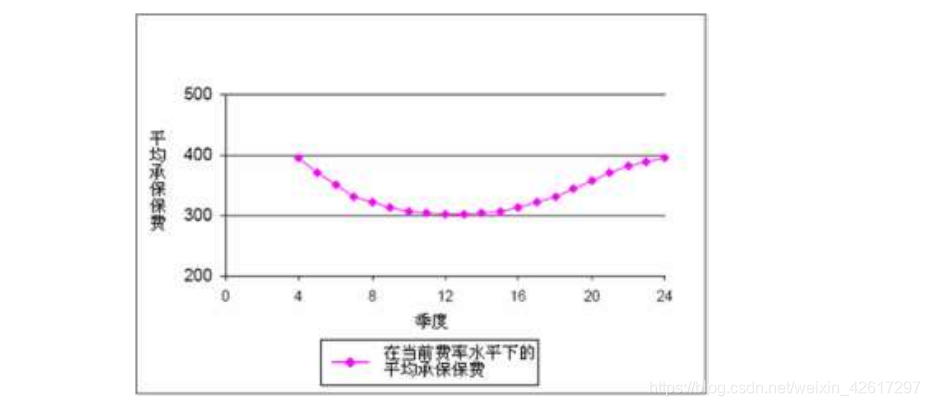
在这里插入图片描述
       两步法用经验期最后一年的平均承保保费除以经验期每一年的平均已赚保费，即可得到第一步的趋势因子。第二步再从经验期最后一年的中点趋势化至未来保险期间的平均承保日期。
       下图显示了经验期为 2000—2002 年，新费率生效日期为 2004 年 1 月 1 日，保单期限为 12 个月时，如何用两步法确定 2001 年平均承保保费的趋势期限。该图表明，未来保险期间的平均承保日期为 2004 年 7 月 1 日，整个趋势期限仍然是 3.5 年，与一步法的趋势期限相同，只不过将整个趋势期限分解成了两个部分。
       在下图中，第一步的趋势因子等于用 2002 年中点上的平均承保保费除以 2001 年中点上的平均已赚保费。由于平均承保日期比平均已赚日期提前半年，所以第一步的趋势因子所对应的趋势期是从 2001 年 1 月 1 日到 2002 年 7 月 1 日，长度为 1.5 年，换言之，该趋势因子相当于把 2001 年 1 月 1 日的平均承保保费调整到了 2002 年 7 月 1 日的平均承保保费水平。注意，第一步得到的趋势因子不是年度趋势因子，而是第一步趋势期的总趋势因子。
在这里插入图片描述
       两步法隐含的一个假设是平均保费序列中的最后一个数值为“真实值”，即未受随机波动的影响。对于索赔频率或索赔强度而言，这种假设未必成立，但对于平均保费而言，随机波动的影响较弱，所以每一个数值都较为稳定，可以近似看作是“真实值”。
       不妨假设经验期内每年的平均已赚保费（调整到了当前费率水平）如下表的第一栏所示，在经验期最后一年（即 2005 年）的平均承保保费为 352.25，新费率的生效日期为 2007年 1 月 1 日，有效期为 1 年，则两步法的应用过程如表 1-26 所示。第一步的趋势因子相当于将经验期各年的平均承保保费水平调整到 2005 年中点上的平均承保保费水平。进一步假设从 2005 年中点到新费率使用期（即 2007 年）中点，平均保费水平每年增长 10%，因此第二步的趋势因子为 1.21，这相当于把 2005 年中点上的平均承保保费水平调整到了新费率使用期中点上的平均承保保费水平。该表最后一栏的总趋势因子相当于把经验期各年的平均承保保费水平调整到新费率使用期中点上的平均承保保费水平。用总的趋势因子乘以经验期各年的平均已赚保费，就相当于把经验期各年的平均已赚保费调整到了 2007 年的平均已赚保费水平。譬如 2002 年的总趋势因子为 1.157，这就意味着在保持当前费率水平不变的情况下，2002 年的平均已赚保费（368.36）到了 2007 年也会增长到 368.36×1.157=426.19。
在这里插入图片描述

1.2.5.2.4 几个特殊问题的处理

       （1）平均承保保费与平均已赚保费的比较
       前面已经指出，在对平均保费水平进行趋势调整时，使用平均承保保费优于使用平均已赚保费，但对它们的差异进行比较仍然是有意义的。
       尽管使用平均承保保费和使用平均已赚保费在总的趋势期限上不存在差异，但是其起讫点不甚相同。平均承保保费法（即在平均保费趋势的分析中使用平均承保保费序列）的趋势期限要比平均已赚保费法（即在平均保费趋势的分析中使用平均已赚保费序列）提前半个保险期间。下图是这两种方法的比较。在该图中，假设经验期为 2000—2002 年，新费率的生效日期为 2004 年 1 月 1 日，保单期限为 12 个月。可以看出，两种方法的趋势期均为 3.5年，但平均承保保费法比平均已赚保费法提前半年。
在这里插入图片描述
       在趋势分析中,不论采用平均承保保费还是平均已赚保费，两步法中第一步的截至日期都是经验期最后一年的中点。从上图可以看出，如果采用平均承保保费法，第一步的趋势期限要长于平均已赚保费法；而第二步的趋势期限要短于平均已赚保费法，这从直观上也说明采用平均承保保费要优于平均已赚保费，因为它缩短了第二步的期限，而此期限中包含了预测值中所固有的不确定性。
       如果采用一步法对保费进行调整，并且在平均承保保费法和平均已赚保费法中使用相同的年度趋势因子，则两种方法将产生相同的结果。但需注意的是，实际上这两种方法的年趋势因子会略有不同，因为平均承保保费的数据要相对更新一些。
       （2）保险期限为 6 个月的保单
       很多公司会承保保险期限为 6 个月的保单。对于 6 个月期的保单而言，第一步的趋势期限要短于保险期限为 12 个月的保单，这是因为对于保险期间较短的保单来说，其平均承保日期和平均已赚日期更为接近（平均承保日期比平均已赚日期提前半个保险期间）。第二步的趋势期限与保险期限为 12 个月保单相同，这是因为未来保险期间的平均承保日期取决于新费率的有效期，与保险期间的长短无关。如果假设新费率的有效期为 1 年，则两种保险期限的第二步趋势期相等。
       下图比较了两种不同保险期限下的趋势期。在该图中，假设经验期为2000—2002年，新费率的生效日期为 2004 年 1 月 1 日。可以看出，对保险期限为 6 个月的保单而言，2001年的总趋势期为 3.25 年，短于 1 年期保单下 2001 年的总趋势期（3.5 年）。
       注意，在保险期限为 6 个月的情形下， 2001 年的第一笔已赚保费来自 2000 年 7 月 2日承保的保单，2001 年的最后一笔已赚保费来自 2001 年 12 月 31 日承保的保单，因此 2001年已赚保费的总承保区间为 18 个月，平均承保日期为 2001 年 4 月 1 日，比 2001 年已赚保费的平均已赚日期（2001 年 7 月 1 日）提前了半个保险期间，即 3 个月。
在这里插入图片描述
       （3）利率敏感型风险基础
       在前面的讨论中，我们假设风险基础是固定的，不受通货膨胀的影响，如汽车保险中的车年。但在某些情况下，风险基础比较复杂，如劳工补偿保险的风险基础通常为工资额，家庭财产保险的风险基础通常为保险金额，而公众责任保险的风险基础通常为营业额等。这类风险基础会受到通货膨胀等经济因素的影响，因此被称为利率敏感型风险基础。对于利率敏感型风险基础，随着通胀的发生，风险单位数会自动增加。例如家庭财产保险通常含有预防通胀的条款，即其保额会随着通胀的发生自动上调一定的百分比，从而使得家庭财产保持在足额保险的状态。这种风险单位数的自动增加类似于保费趋势，降低了费率上调的实际需求。
       在预测未来的期望赔付率时，需要对经验期的索赔频率、索赔强度和平均保费的变化进行调整。为了获得合理的赔付率预测值，对赔付率的分子和分母所进行的调整必须一致。
       索赔频率趋势是指每份保单或每个风险单位的平均索赔次数的变化；索赔强度趋势是指每次索赔的平均赔付额的变化；索赔频率趋势和索赔强度趋势的乘积代表了纯保费的趋势。注意，在乘积的过程中，平均索赔次数被消去了，因此纯保费的趋势是指每份保单或每个风险单位的平均赔付额的变化（这与索赔频率趋势的度量基准是一致的，即每份保单或每个风险单位）。为了获得合理的赔付率预测值，还需要对赔付率的分母做出适当调整，使平均保费的变化基准也为每份保单或每个风险单位。换言之，在对保费序列进行趋势分析时所使用的风险基础必须和进行索赔频率分析时所使用的风险基础一致，或者都用每份保单，或者都用每个风险单位。
       如果对索赔频率、索赔强度和平均保费的趋势分别进行调整，其净效应相当于调整赔付率的变化趋势。因此在某些险种中，也可以直接对赔付率进行趋势调整，此时，就无需考虑风险基础的选择问题了。
       下面以下表1中所示的劳工补偿保险为例，对风险基础的选择进行说明。在该表中，每 100 元工资额为一个风险单位，工资每年增长 4％，赔款每年增长 5％。为了简化分析，假设除了工资额的增长外，没有影响保费趋势的其他因素。
在这里插入图片描述
       假设其他变量的增长趋势下表2所示。

       在表2中，每百元工资额为一个风险单位，所以风险单位数的增长趋势等于工资额的增长率，均为 4%。每个雇员的平均保费也会随着工资额的增长而增长，所以年度增长趋势为4%。由于索赔次数保持不变，而风险单位数每年增长 4%，所以每个风险单位的索赔频率每年增长-3.85%，即[1/(1+4%)-1]=-3.85%。前面已经假设赔款每年增长 5%，所以在索赔次数和雇员数保持不变的情况下，每次索赔的平均赔付额和每个雇员的平均赔付额每年也将增长5%。由于赔付额每年增长 5%，而风险单位数每年增长 4%，所以每个风险单位的平均赔付额每年将增长 0.96%，即[(1+5%)/(1+4%)-1]=0.96%。由于每个风险单位的平均赔付额每年增长 0.96%，而每个风险单位的纯保费保持不变，所以赔付率的年度增长趋势为 0.96%。
       在该例中，虽然雇员的数量没有增加（始终为 10），但是由于工资额的增加导致了风险单位数的增加（第 3 列和第 4 列），其中每百元工资额为一个风险单位。从表2可以看出，每个风险单位的平均保费序列并不存在保费趋势（第 9 列），但是每个雇员的平均保费存在着正的保费趋势（第 10 列）。
       与保费趋势类似，赔款趋势中的索赔频率部分既可以用每百元工资额为基准（第 11 列），也可以用每个雇员为基准（第 12 列），而索赔强度的基准始终为每次索赔（第 13 列）。为了便于讨论，可以将索赔频率趋势和索赔强度趋势合并为纯保费趋势，其基准可以为每百元工资额（第 14 列）或每个雇员（第 15 列）。
       根据表1的数据，计算未来的期望赔付率可以采取不同的方法。下面假设新费率从第 7 年的 1 月 1 日生效，有效期为 1 年，现在需要预测新费率使用期的期望赔付率。可以采用下述三种方法。
       方法 1：直接用赔付率趋势对经验赔付率进行调整，相应的计算公式为： $调整后的赔付率=经验赔付率×（1+赔付率趋势）^{趋势年数}$
       新费率使用期从第 7 年的 1 月 1 日开始，有效期为 1 年，所以已赚保费的平均日期（即平均已赚日期）和事故发生的平均日期均为第 7 年的年末，即在新费率使用期，赔付率对应的平均日期为第 7 年的年末。从第 5 年的中点到第 7 年的年末正好是两年半，所以第 5 个事故年的趋势期为 2.5 年。
       在这种方法下，新费率使用期的期望赔付率预测值为 70.9％，如表3所示。
在这里插入图片描述
       方法 2 ：分别用赔款趋势和保费趋势对经验赔付率进行调整，赔款趋势和保费趋势的基准均为每百元工资额。这种方法的结果和方法 1 相同，如表4 所示，但其优点是可以对赔付率的各个组成部分（索赔频率和索赔强度）分别选择趋势因子。方法 2 的计算公式如下： $调整后的赔付率=经验赔付率×[（1+赔款趋势）/(1+保费趋势)]^{趋势年数}$
在这里插入图片描述
       方法 3 ：分别用赔款趋势和保费趋势对经验赔付率进行调整，但赔款趋势和保费趋势的基准均为每个雇员。这种方法与方法 2 的原理相同，只是在计算赔款增长趋势和保费增长趋势时，以每个雇员为计算基准。方法3的计算公式和计算结果与方法2 完全相同，如表5所示。
在这里插入图片描述
       由此可见，在对经验赔付率进行调整时，可以采用不同的方法，但需要特别注意的是，在选择赔款增长趋势和保费增长趋势时，必须使用相同的计算基准，譬如在前述方法 2 中都为每百元工资额，方法 3 中都为每个雇员。如果在计算赔款增长趋势时使用每百元工资额，而在计算保费增长趋势时使用每个雇员，即两个增长趋势选择不同的计算基准，其结果就会出现偏差。

二、预测最终赔款与直接理赔费用、最终索赔次数

2.1实操

2.1.1 预测最终赔款与直接理赔费用

已知2002-2007年的已发生赔款与直接理赔费用的流量三角形如表5所示，用损失进展法预测各年的最终赔款。首先计算赔款与直接理赔费用进展因子，这里把所有年份进展因子的简单平均值作为选定进展因子，累计相乘得到最终进展因子，然后用各年在2007年12月31日的已发生赔款乘以各自的最终进展因子，即得到各年的最终赔款（见表7）
在这里插入图片描述

2.1.2 预测最终索赔次数

与预测最终赔款与直接理赔费用相同，预测最终索赔次数同样可以采用进展法，首先计算进展因子，然后得到各年的最终索赔次数。
在这里插入图片描述

2.2 理论补充

2.2.1 赔款和费用

       赔款是指根据保险合同的约定应当由保险公司支付给索赔人的款项，包括已付赔款和未决赔款两部分。已付赔款是指已经支付给索赔人的款项，而未决赔款是保险公司预期需要支付给索赔人的款项。未决赔款包括逐案估损准备金（case reserve）、已发生未完全报案赔款（incurred but not enough reported, IBNER）和已发生未报案赔款（incurred but not reported,IBNR）。在实务中，已发生未完全报案赔款也可以作为已发生未报案赔款的一部分处理。逐案估损准备金是保险公司根据已经报案的事故而估计的在未来将要支付的赔款，也称作已发生已报案赔款准备金。已付赔款与逐案估损准备金之和也被称作已报案赔款（reported loss）或已发生赔款（incurred loss），即已报案赔款=已付赔款+逐案估损准备金。
       已发生未完全报案赔款是指考虑到逐案估损准备金可能存在不足而对逐案估损准备金进行的调整。如果在已报案赔款的基础上增加上已发生未完全报案赔款和已发生未报案赔款，就得到了最终赔款（ultimate loss），即最终赔款=已报案赔款+IBNR 准备金+IBNER 准备金
       最终赔款是指保险公司向索赔人最终需要支付的赔款。
       索赔频率（claim frequency）是指在一定时期内（通常为一年），每个风险单位的索赔次数，通常用索赔总次数和风险单位数之比进行估计。
       索赔次数既可以按照事故日期（accident date）统计，也可以按照报案日期(report date)统计。事故日期是指保险事故发生的日期，而报案日期是指保险人收到索赔申请的日期。因此，在使用索赔频率这个概念时，应该明确索赔次数的统计含义。
       需要注意的是，在一定时期内发生的索赔次数需要在保险期限结束后再经过一段时间才能确切统计出来，因为保险事故从发生到报案通常存在时间延迟。不同险种的报案延迟时间长短不一，一般而言，财产保险的报案延迟时间较短，而责任保险的报案延迟时间较长。因此，在费率厘定实务中，通常需要根据已经报案的索赔次数来预测最终的索赔次数，并根据预测的索赔次数计算索赔频率。
       索赔强度（claim severity）是指每次索赔的赔款，通常用赔款总额与索赔次数之比进行估计，因此在实务中也称之为案均赔款。从严格意义上讲，在估计索赔强度时，赔款应该是最终赔款，索赔次数也应该是最终索赔次数。由于报案延迟和理赔延迟的影响，最终赔款数据通常需要在保险期限结束以后经过较长时间才能得到。某些险种（如责任保险）的理赔延迟可能比较严重，有时需要经历旷日持久的诉讼程序，因此在费率厘定实务中，最终赔款也需要根据已付赔款或已报案赔款进行预测。显然，除了报案延迟的影响外，最终赔款的预测还受到理赔延迟的影响，所以相对于最终索赔次数的预测而言，最终赔款的预测难度更大。
       在保险业务的经营过程中，保险公司除了需要支付各种赔款之外，还会发生各种各样的费用，如承保费用和理赔费用。
       承保费用包括代理人佣金、一般管理费用、广告费用和税金等。代理人佣金是保险公司支付给保险代理人的费用，通常按照承保保费的一定比例计算。在计算代理人佣金时，也可能会考虑代理人所招揽的业务质量，并区分新业务和续保业务的差异。在费率厘定中，承保费用通常被区分为固定费用和变动费用两大类。固定费用是指与纯保费的大小无关的费用，变动费用是指与纯保费的变动直接相关的费用。
       理赔费用是保险公司在理赔和结案过程中发生的费用，一般分为两种：直接理赔费用和间接理赔费用。直接理赔费用（Allocated Loss Adjustment Expense，简称 ALAE）是指与具体案件的理赔直接相关的费用，如勘查费和诉讼费等；间接理赔费用（Unallocated LossAdjustment Expense，简称 ULAE）是指理赔部门的整体运营费用，包括理赔部门的薪金、办公费用和数据处理费用等，不能分摊给具体的赔案。在厘定保险费率时，通常将直接理赔费用与赔款合并在一起处理，而将间接理赔费用按赔款的一定百分比进行分配。

2.2.2 赔款数据的汇总

       在赔款数据的汇总中，首先需要明确三个概念：统计指标（如已付赔款或已报案赔款），汇总方法（如日历年度法、事故年度法、保单年度法或报案年度法），以及汇总时期。汇总时期通常由一个会计期间和一个评估日期来确定。会计期间通常与财务报表的时期相一致，如一个月，一个季度或一个日历年度等。评估日期是对赔款做出评估的日期，不一定就是会计期间的终点。评估日期通常用距离会计期间起始点的月数来表示，譬如，如果要汇总 2009事故年的已报案赔款数据，数据的截至日期是 2010 年 6 月 30 日，即已报案赔款是基于 2010年 6 月 30 日的信息进行评估的，则相应的会计期间就是 2009 日历年度，而评估日期就是2010 年 6 月 30 日，即距离 2009 事故年的起始点为 18 个月，因此相应的汇总数据可以称作截至 18 个月末的 2009 事故年的已报案赔款。
       赔款数据可以根据不同的方法进行汇总。如果按日历年度汇总赔款数据，则日历年已付赔款就包括了该日历年支付的所有赔款，而日历年已报案赔款就等于日历年的已付赔款加上日历年逐案估损准备金的提转差。在日历年度末，就可以完全确定日历年的已付赔款和已报案赔款数据。
       如果按照事故年汇总赔款数据，则不论保单是何时签发的，也不论索赔的报案日期，只要事故发生在哪年，就将赔款归集在哪年。事故年的已付赔款就是对发生在当年的事故所实际支付的赔款，而事故年的已报案赔款就等于事故年已付赔款再加上在评估日对当年已经发生事故提取的逐案估损准备金。与日历年赔款数据不同，事故年赔款数据在事故年结束之后还有可能发生变化，主要原因是延迟索赔的报案和赔付，以及逐案估损准备金的调整。
       如果按照保单年度汇总赔款数据，则可以将同一年度签发的保单所发生的赔款归集在一起。保单年的已付赔款就是同一年度签发的保单实际已经支付的赔款。保单年的已报案赔款就是保单年的已付赔款加上在评估日确定的该保单年所签发保单的逐案估损准备金。如同事故年赔款数据一样，在保单年结束以后，赔款数据也可能因为延迟索赔的报案和逐案估损准备金的调整而发生变化。对于一年期保单而言，保单年的索赔可以横跨两年，因此，基于已知索赔信息对未来的赔款进行预测具有更大的不确定性。
       如果按照报案年汇总赔款数据，赔款数据是基于报案日期进行归集的。按报案年汇总数据不会产生已发生未报案赔款（IBNR），但已发生未完全报案赔款（IBNER）仍然存在。报案年数据通常只用于索赔报案制保单的定价。
       下面通过一个例子来说明在不同方法下已报案赔款数据的汇总。假设保险公司在 2009年之前的准备金为零，下表是该公司全部的索赔信息。
在这里插入图片描述

       根据上表中的信息，如果按照日历年汇总已报案赔款数据，则各个日历年的已报案赔款如下：
       2009 日历年的已报案赔款=2009 日历年的已付赔款+2009 日历年末的逐案估损准备金-2009 日历年初的逐案估损准备金 = 0+10000-0=10000。
       2010 日历年的已报案赔款=2010 日历年的已付赔款+2010 日历年末的逐案估损准备金-2010 日历年初的逐案估损准备金 = （1000+7000+5000+8000）+（2500+4000）-10000=17500。
       2011 日历年的已报案赔款=2011 日历年的已付赔款+2011 日历年末的逐案估损准备金-2011 日历年初的逐案估损准备金 = （3000+1000）+0-（2500+4000）= -2500
       如果按照事故年汇总已报案赔款数据，评估日为 2011 年 12 月 31 日，则由上表可知，2009 事故年只发生了一次事故，2010 年也只发生了一次事故，因此在计算这两个事故年的已报案赔款时，分别只需考虑一次事故，计算过程如下：
       2009 事故年截至 2011 年 12 月 31 日的已报案赔款=2009 事故年的已付赔款+2009 事故年的逐案估损准备金 = （1000+7000+3000）+0=11000。
       2010 事故年截至 2011 年 12 月 31 日的已报案赔款=2010 事故年的已付赔款+2010 事故年的逐案估损准备金 = （5000+8000+1000）+0=14000。
       如果按照保单年汇总已报案赔款数据，评估日为 2011 年 12 月 31 日，则从上表可知，只有 2009 年签发了 2 份保单，所以只能计算 2009 保单年的已报案赔款，其他保单年的已报案赔款为零。2009 保单年的已报案赔款可以如下计算：
       2009 保单年截至 2011 年 12 月 31 日的已报案赔款=已付赔款+逐案估损准备金=（1000+7000+3000+5000+8000+1000）+0=25000。
       如果按照报案年汇总已报案赔款数据，则 2009 报案年的已报案赔款只包括第一次索赔。截至 2009 年 12 月 31 日，2009 报案年的已报案赔款为 10000，就是第一次索赔在 2009 年末的逐案估损准备金。截至 2010 年 12 月 31 日，2009 报案年的已报案赔款为 10500，包括已经支付的赔款（1000+7000）和 2010 年末的逐案估损准备金（2500）。第二次索赔的报案日期在 2010 年，所以相应的赔款数据应该归集在 2010 报案年。

2.2.3 费用数据的汇总

费用数据可以分解为承保费用和理赔费用，理赔费用又可以进一步分解为直接理赔费用和间接理赔费用。对于直接理赔费用，通常将其与赔款数据合并在一起处理，所以其汇总也是与赔款数据合并在一起进行的。对于间接理赔费用，通常按照日历年度进行汇总，并将其按照赔款的一定比例分摊在不同保单的赔款数据中，用于计算保单的纯保费。承保费用通常也是按照日历年度汇总的，将其分解为固定费用和变动费用以后，通过不同的方式附加在纯保费之上。

2.2.4 赔款数据的调整

       在费率厘定中，需要预测新费率使用期的期望赔款（即纯保费），通常的做法是对经验期的赔款数据进行调整。调整的内容主要包括下述三个方面：
       （1）剔除经验数据中的异常损失，然后将其在一个较长的时期内分摊。
       （2）应用链梯法等技术将经验期的已付赔款或已报案赔款进展到最终赔款。
       （3）根据保障水平的变化和通货膨胀等因素对经验期的赔款进行趋势调整，得到新费率使用期的期望赔款。
       在实际应用中，对经验数据进行上述调整的先后顺序需要根据实际情况来确定，没有固定的顺序。譬如，如果应用巨灾模型来估计新费率使用期的期望巨灾赔款，那么可以直接将其与趋势化处理后的不含巨灾损失的最终赔款相加，得到未来时期的纯保费估计值。但是，如果将巨灾模型估计的期望巨灾赔款与经验期的非巨灾赔款相加后再进行趋势化处理，就会导致对期望巨灾赔款的重复性调整。

2.2.4.1 异常损失和巨灾损失的处理

       1. 异常损失的处理
       异常损失是指一份保单所提出的高额索赔。异常损失的发生频率很低，但损失金额很大。如果经验损失数据中包含异常损失，用其预测未来期望赔款的稳定性就会较差。因此在费率厘定过程中，可以把经验数据中的异常损失完全剔除，或者仅仅保留特定限额（称作门限值）以下的部分损失，并在此基础上预测未来的期望赔款。当然，这时预测得到的期望赔款是不含异常损失的。为了在上述期望赔款中附加上异常损失，可以把经验数据中的异常损失在一个较长的时期内分摊，然后再将其附加在上述期望赔款中。
       某些情况下，在对经验损失数据进行截断处理时，可以把门限值设定为保单的基本赔偿限额。此时，计算得到的费率应该是基本限额下的费率，因此需要在费率厘定中把经验期的保费数据也调整到基本限额水平，也就是在基本限额下重新计算经验期每个风险单位的保费。
       当然，理想的门限值应该是这样一个损失金额，即如果在费率厘定中包含门限值以上的损失，费率厘定结果就会不稳定，因此，理想的门限值有可能远远大于保单的基本赔偿限额。
       如果合适的门限值不是基本限额，则可以通过分位数的方法选择门限值，譬如，可以把损失分布的 99%分位数确定为门限值。对于某些保险产品（如财产保险），保险金额是随着保险标的的价值而变化的，此时，可以把门限值确定为保险金额的一个比例，这可能比确定一个固定的门限值更为合适。
       对于超过门限值的赔款，应该在一个较长的时期内分摊，然后再将其附加在不含异常损失的期望赔款之上。这个较长的时期到底应该是多少年，取决于不同的保险产品，也与保险公司的业务规模密切相关。
       应该注意的是，时期越久远的经验数据，与未来的相关性就越低，其在费率厘定中的应用价值也就越低。
       下表是计算异常损失附加因子的一个简例。该例假设门限值为 100,000，即超过这个金额的损失被看做是异常损失。对于异常损失中超过门限值的部分进行截断处理，可以得到门限值以内的赔款金额如该表的第 6 列所示，而超过门限值的部分如该表的第 5 列所示。用第 5 列的超过门限值的部分除以第 6 列门限值以内的赔款，就可以求得各年异常损失所占比率。计算经验期内各年异常损失比率的平均值，即用第 5 列的总和除以第 6 列的总和，就可以得到异常损失比率的平均值为 2.37%。由此即可求得异常损失的附加因子为（1+2.37%）= 1.0237。这种处理异常损失的方法隐含着一个假设，即异常损失在较长的时期内是相对稳定的。在本例中，也就意味着，从一个较长的时期来看，超过 100,000 的损失与 100,000 以内的损失之比稳定在 2.37%附近。因此，在求得正常纯保费（即不考虑异常损失）的情况下，将其乘以异常损失附加因子（1.0237），即可得到包含异常损失的纯保费。
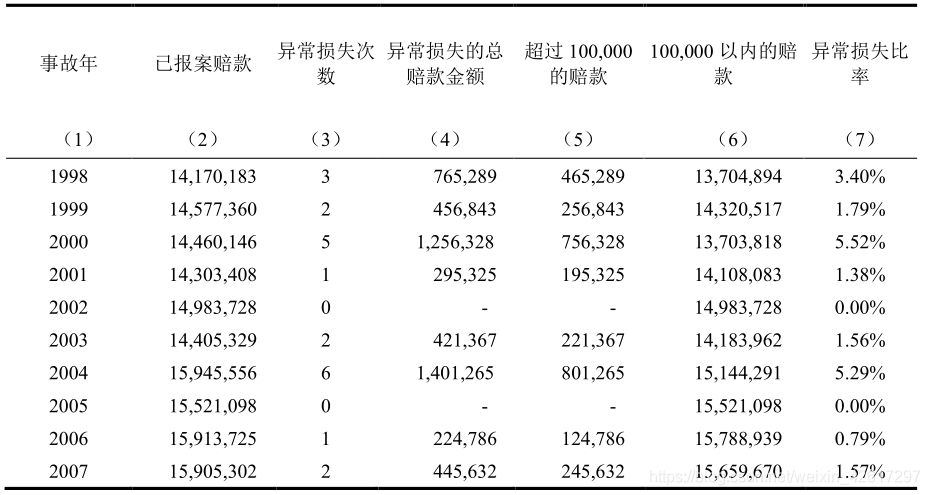
在这里插入图片描述

       注意，在上表的计算中，假设对已报案赔款已经进行了趋势化处理，即考虑了通货膨胀等因素对已报案赔款的影响。
       上例是计算异常损失附加因子的一种简单方法，在实务中，也可以考虑对损失数据建立分布模型，然后基于分布模型计算异常损失附加因子。
       2. 巨灾损失的处理
       如同对异常损失的处理一样，在费率厘定过程中，首先需要从经验数据中剔除巨灾损失数据的影响，然后根据巨灾损失附加因子来预测未来的期望赔款。
       如前所述，异常损失是指一份保单所提出的高额索赔，而巨灾损失是指一次事故所导致的大量保单同时提出的高额索赔。
       计算巨灾损失附加因子的方法与巨灾的类型有关，通常可以分为两大类，一类是巨灾模型的方法，另一类是非巨灾模型的方法。
       非巨灾模型方法主要适用于那些在数十年内具有一定规律性的巨灾事故。譬如在车损险中，冰雹造成的车辆损害索赔就是这种类型的巨灾损失。虽然在短期内很难预测冰雹造成的车辆损失，但在一个较长的时期内（如 10-30 年），这种损失具有一定的规律性，因此可以采用前述关于异常损失的处理方法。
       巨灾模型方法主要适用于那些非常偶然的巨大损失事故，如地震和飓风等。对于这类损失事故，即使有 30 年的经验数据也很难预测其期望损失，因此通常使用巨灾模型方法。巨灾模型是由保险专家、气象专家和工程师等各种专业人士合作建立的一种随机模型，该模型可以模拟各种不同强度的巨灾事故对各种被保险财产可能造成的损害程度。因此，基于巨灾模型的模拟结果，就可以预测巨灾事故可能给保险公司每年造成的期望损失，并据此计算巨灾损失附加因子，然后将其附加到非巨灾损失的估计值中，就可以得到包含有巨灾损失的纯保费。
       对于大多数年份，实际的巨灾损失会小于每年的期望巨灾损失附加，但在个别年份，实际的巨灾损失可能会远远大于期望的巨灾损失附加。
       3. 再保险的处理
       再保险可以分为比例再保险和非比例再保险。在比例再保险中，如果原保险公司将其保费和赔款都按相同的比例分摊给再保险人，在费率厘定中就无需考虑比例再保险的影响。但是，如果再保险人认为原保险费率是不充足的，从而提高了再保险的报价，此时也需在费率厘定中考虑再保险报价的影响。
       在非比例再保险中，再保险人承诺负责补偿原保险公司的一部分赔款（即再保险摊回），同时从原保险公司收取再保险费。这里的再保险赔款与再保险费之间没有确定的比例关系，因此，在费率厘定中，应该从预测的赔款中扣除再保险赔款，同时从总保费中扣除相应的再保险费。另一种处理方法是，在总平均费率水平的厘定中，把再保险的净成本（即再保险费减去再保险赔款后的剩余部分）作为一个费用项目处理。

2.2.4.2 保障范围与补偿水平的调整

       在基于经验损失数据对未来的期望赔款进行预测时，必须考虑到保单的保障范围和补偿水平是否在将来会发生变化。如果未来的保障范围或补偿水平不同于经验期，就必须根据新的保障范围或补偿水平对经验期的赔款数据进行适当的调整。保障范围的变化既可以是增加或减少承保的风险类型（例如从保单的保障范围中剔除了盗窃损失），也可以是增加或减少保险金额。补偿水平的变化在一些强制保险中比较常见，譬如在交强险中，补偿水平是由有关法律规定的，因此法律法规的变化就有可能导致补偿水平的变化。
       保障范围和补偿水平的变化对未来期望赔款既有直接影响，也有间接影响。一般而言，直接影响比较容易量化，而对间接影响的度量通常只能基于精算师的职业判断。譬如，下调免赔额的直接影响就是未来期望赔款的上升，而且在已知损失分布或经验数据比较充足的情况下，未来期望赔款的上升幅度也是比较容易计算的。但是，免赔额下调的间接影响可能是投保人的行为发生了变化，但这种变化很难量化处理。
       Werner & Modlin（2009）以美国劳工补偿保险为例，介绍了补偿水平变化对期望赔款的影响及其调整方法。该例的有关假设如下：
       （1）补偿水平是雇员伤残前工资的 66.7%
       （2）目前的周平均工资是 1000 美元
       （3）最低补偿标准是周平均工资的 50%
       （4）最高补偿标准将从经验期周平均工资的 100%下降到未来周平均工资的 83.3%
       （5）伤残雇员根据其工资水平的分布如下表所示。
在这里插入图片描述
       为了计算最高补偿标准下调的直接影响，就需要计算对于上表中的雇员，在最高补偿标准下调之前和之后的补偿分别是多少。
       首先讨论在最高补偿标准下调之前的情况。此时的最低补偿标准是周平均工资的50%，即为 500 美元。在当前的补偿水平（66.7%）下，因为1000×75%×66.7%=500 美元，所以周工资在平均周工资 75%以下的雇员将领取最低补偿。这类雇员有 31 人，补偿金额为 31×500=15500 美元。
       当前的最高补偿标准是平均周工资的100%，即为1000美元。在当前的补偿水平（66.7%）下，周工资在平均周工资 150%以上的雇员将领取最高补偿，因为 1000×150%×66.7%=1000美元。这类雇员有 11 人，补偿金额为 11×1000=11000 美元。
       其他58个雇员落在最低补偿和最高补偿之间，他们将按照其周工资的66.7%领取补偿，补偿金额为（23950+23048+16500）×66.7%=42354 美元。
       因此，在调整最高补偿标准之前，总的补偿金额为 15500+11000+42354=68854 美元。
       如果把最高补偿标准从当前的 100%下调到 83.3%，即为 833 美元，则周工资大约在平均周工资 125%以上的雇员将领取最高补偿，因为1000×125%×66.7%=833.75 美元。这类雇员有 23 人，补偿金额为 23×833=19159 美元。领取最低补偿的雇员不会受到任何影响，他们的补偿金额仍然为 15500 美元。落在最低补偿和最高补偿之间的雇员人数还剩 46 人，他们按其周工资的 66.7%领取补偿，补偿金额为（23950+23048）×66.7%=31348 美元。因此，在下调最高补偿标准以后，总的补偿金额为19159+15500+31348=66007 美元。
       由此可见，如果下调最高补偿标准，则总的补偿金额将从 68854 美元下降到 66007 美元，下降幅度为 4.1%，即保险公司的赔款会降低 4.1%。
       在求得补偿标准的变化对赔款金额的直接影响以后，精算师还需要考虑这种影响发生的时间和其他有关的细节，从而对经验赔款数据进行恰当的调整。这里首先需要考虑的问题是补偿标准的变化将从何时开始。通常有两种情况，一种情况是规定从某个日期开始签发的新保单都按照新的补偿标准进行赔偿，另一种情况是规定从某个日期开始新发生的索赔都按照新的补偿标准进行赔偿。
       首先考虑第一种情况，即假设新的赔偿标准将从 2010 年 8 月 15 日实施，且适用于从该日开始承保的保单。这种情况如下图所示，始于 2010 年 8 月 15 日的那条斜线表示该日承保的保单在 2011 年 8 月 14 日到期。
在这里插入图片描述
       为了计算各个事故年的调整因子，可以应用平行四边形方法。注意，在该图中，事故年被划分成了四个事故季度，其目的是为了在应用平行四边形方法时弥补事故发生过程可能存在季节性波动的影响。如同当前费率水平调整因子一样，计算各个事故季度的赔款调整因子可以应用下述公式： $赔款调整因子=\frac{当前的赔款水平}{经验期的平均赔款水平}$
       假设补偿标准调整前的赔款水平是 1，补偿标准调整后的赔款水平是 1.04。对于 2010年的第 3 个事故季度而言，补偿标准调整后的赔款所占比例为：0.5×0.125×0.125 = 0.0078
       补偿标准调整前的赔款所占比例为：0.25-0.0078 = 0.2422
       因此，2010 年第 3 个事故季度的赔款调整因子为：
        $2010年第3个事故季度的赔款调整因子=\frac{1.04}{1×\frac{0.2422}{0.25}+1.04×\frac{0.0078}{0.25}}=1.0387$
       其他各个事故季度的赔款调整因子也可类似计算。
       前面讨论了如何计算事故年度的赔款调整因子。如果需要计算上述补偿标准的变化对保单年度赔款的影响，可以参见下图计算保单年度的赔款调整因子。
在这里插入图片描述
       仍然以 2010 年第 3 个保单季度为例，赔款调整因子为：
        $2010年第3个保单季度的赔款调整因子=\frac{1.04}{1×0.5+1.04×0.5}=1.0196$
       对于 2010 年第 3 个保单季度之前的赔款，调整因子都为 1.04，而对于 2010 年第 3 个保单季度之后的赔款，因为都已经按照新的补偿标准进行了赔偿，所以无需调整。
       在前面的讨论中，我们假设从某个日期开始签发的保单都按照新的赔偿标准进行赔偿。如果新实施的法律规定，从某个日期（如上例中的 2010 年 8 月 15 日）开始发生的索赔都按照新的赔偿标准进行赔偿，则事故年度的赔款如下图所示。
在这里插入图片描述
       仍然以 2010 年第 3 个事故季度为例，赔款调整因子为：
        $2010年第3个事故季度的赔款调整因子=\frac{1.04}{1×0.5+1.04×0.5}=1.0196$
       相应地，保单年度的赔款如下图所示。仍然以 2010 年第 3 个保单季度为例，相应的赔款调整因子为：
        $2010年第3个保单季度的赔款调整因子=\frac{1.04}{1×\frac{0.0078}{0.25}+1.04×\frac{0.2422}{0.25}}=1.0012$
在这里插入图片描述

2.2.4.3 最终赔款的预测

       在根据经验期的已付赔款或已报案赔款对经验期的最终赔款进行预测时，最简单的方法是损失进展法（loss development）。损失进展法的假设条件如下：保险事故发生以后，索赔将经历“未报告→已报告但未赔付→已赔付”这一顺序发展，而且这一过程在一定时期内是平稳的，因此可以基于历史索赔数据的统计分析，对未来的损失进展情况和最终赔款进行预测。
       如果把已付赔款分别按事故年和进展年进行排列，观察数据将形成一个流量三角形。下表是应用某险种的累积已付赔款数据所构造的流量三角形。在该表中，每行表示相同的事故年，从左到右表示每个事故年的累积已付赔款在不断增加
在这里插入图片描述

       根据上述流量三角形，可以计算出相邻两个进展年之间已付赔款的增长情况。譬如，用第 1 个进展年的累积已付赔款除以第 0 个进展年的累积已付赔款，就可以得到累积已付赔款在 1 年内的增长比率，这个增长比率被称作进展因子。
在这里插入图片描述
       注意，在上表中，平均值不是各年进展因子的简单平均，而是一种加权平均。上述加权平均数事实上就是第1个进展年的累积已付赔款之和与第0个进展年的累积已付赔款之和的比率。
       在计算进展因子的平均值时，除了应用上述的加权平均方法外，在实际应用中还可以根据具体情况采用所有年度的简单平均、近几年的简单平均、剔除最大最小值后的简单平均、所有年度的几何平均等方法。
       上表中最后一行的进展因子是根据倒数第二行的平均值选定的，同时考虑了已付赔款和经济环境在未来的变化。这一行数据将用于对未来已付赔款进行预测。对累积已付赔款的预测值如下表所示。譬如， 2002 事故年在当前的累积已付赔款是 5718，而 3－4 的进展因子为 1.10，4－5 的进展因子为 1.10，所以 3－5 的进展因子为 1.1×1.1 ＝ 1.21，因此在第 5 个进展年末的累积已付赔款应为5718×1.21＝6919。在下表中，最后一列即为各个事故年的最终赔款。当然，这里假设第 5 个进展年以后将不再有赔款支出。如果实际情况并非如此，就需要考虑尾部因子，计算第 5 个进展年以后的赔款支出。
在这里插入图片描述

三、计算索赔强度、索赔频率的趋势因子

3.1实操

用事故年2002-2007的最终赔款与直接理赔费用的预测值除以最终索赔次数的预测值，可以得到各年最终索赔强度的预测值。采用线性最小二乘拟合法，可以得到各年索赔强度的拟合值。拟合最终索赔强度的趋势线为 $y = a x + b$ ，其中， $x = 事故年 - 2002$ ， $y$ 是最终索赔强度的预测值。用2007年的拟合值除以2006年的拟合值可以估计索赔强度的年度增长趋势因子。
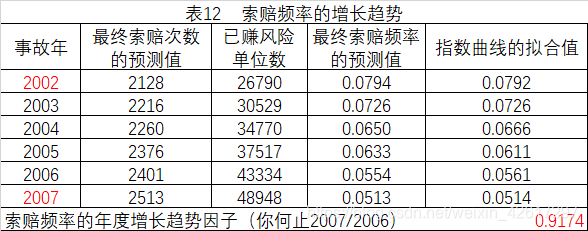
在这里插入图片描述
用事故年2002-2007的最终索赔次数预测值除以已赚风险单位数可以得到最终索赔频率的预测值。然后采用指数最小二乘拟合法，可以得到各年索赔频率的拟合值。指数趋势线为 $y=a e^{bx}$ ，其中， $x = 事故年 - 2002 + 1$ ， $y$ 为最终索赔品类的预测值。用2007年的拟合值除以2006的拟合值就可以估计索赔频率的年增长趋势因子。
在这里插入图片描述

3.2理论补充

3.2.1 赔款数据的调整

3.2.1.1赔款的趋势调整

       在获得最终赔款的预测值以后，还需要分析期望赔款从经验期到新费率使用期的变化趋势，并应用这种变化趋势对上述的预测值进行调整。
       在一般情况下，需要把期望赔款（即纯保费）分解为索赔频率和索赔强度的乘积，并对索赔频率和索赔强度的变动趋势分别进行分析，这有助于获得更多的信息。
       精算师通常将观察到的数据转化为一条合适的曲线来反映索赔频率或索赔强度的发展趋势。这里需要特别强调“合适”二字，否则对发展趋势的判断会产生严重偏差。所谓的“合适”并非是指对观察数据的拟合效果很好，而要结合实际情况进行综合考察。有时候，拟合效果最好的曲线并非是最合适的，因为它所表示的发展趋势在未来不可能出现，而那些拟合效果并非最好的曲线可能更加合理地反映了索赔频率或索赔强度的未来发展趋势。
       在费率厘定实务中，预测索赔频率或索赔强度趋势的两个常用模型是线性模型和指数模型，它们分别具有下述的形式：
在这里插入图片描述
       可见，这两个模型都可以表示成线性函数的形式，并用标准的最小二乘法估计其未知参数。
       无论是线性模型还是指数模型都适用于上升的趋势。然而，如果观察到的趋势是下降的，那么使用线性模型将在未来出现负值。由于索赔频率、索赔强度和纯保费都是非零的，所以在这种情况下，一般不宜使用线性模型，而应该使用指数模型或其他模型。
       此外，如果经验损失数据受到赔偿限额的影响，就必须在索赔强度的趋势分析中予以考虑。下面通过一个简例来说明索赔强度的趋势变化与赔偿限额的关系。
       假设某风险的损失金额在 50 万元以内波动，现有三份保单为此风险提供保障。对于每次损失，第一份保单负责赔偿 0～10 万元的损失；第二份保单负责赔偿 10～25 万元之间的损失；第三份保单负责赔偿 25～50 万元之间的损失。假设该风险在保险期间发生了 3 次损失，损失金额分别为 5 万、20 万和 40 万，则每份保单承担的赔款如下表所示。
在这里插入图片描述
       如果所有损失金额由于通胀的影响，平均上升了 10%，则每份保单承担的赔款如下表所示。

       可见，尽管损失金额平均上升了 10%，但每份保单赔款的上升幅度并不相同。承担的损失层次越高，索赔强度的变化幅度越大。其实这是很好理解的，因为对于承担较低层次损失的保单，它所承担的责任已经接近饱和，所以损失金额上升对它的影响较小。

四、计算目标赔付率

4.1实操

由目标赔付率的计算公式 $T=\frac{1-V-Q}{1+G}$ 可知，为了计算目标赔付率，首先需要计算费用附加率 $V$ ，以及间接理赔费用占赔款与直接理赔费用的比例 $G$ 。在此例中，假设利润附加率 $Q$ 为0.目标赔付率的计算过程如下表13所示：
在这里插入图片描述

4.2理论补充

4.2.1赔付率和其他比率

       赔付率（loss ratio）是指在每单位保费中用于支付赔款的部分，通常用赔款与保费之比进行估计。更严格地讲，为了实现保费和赔款之间的配比关系，应该用最终赔款与已赚保费之比进行估计。在实际应用中，由于实际数据的限制，赔款有可能采用已付赔款、已报案赔款或预的最终赔款，而保费也有可能采用承保保费或已赚保费。显然，对于保费和赔款的不同选择将导致不同的赔付率估计值。例如，基于已付赔款和承保保费计算的付率，与基于最终赔款和已赚保费计算的赔付率，就有很大不同，尽管这两个都可以简称为赔付率。最常使用的一个赔付率可能是基于已报案赔款和已赚保费估计的赔付率。此外，某些保险公司在计算赔付率时将理赔费用也包含在赔款之中，此时的赔付率被称作赔款和理赔费用率（loss and LAE ratio）。在传统上，许多保险公司通过赔付率的高低来评价当前费率水平的充足性。
       在保险和精算实务中，除了赔付率之外，还有一些比率指标也比较常用，如理赔费用率、承保费用率、经营费用率、综合成本率、续保率和签约率等，下面分别予以介绍。
       理赔费用率（loss adjustment expense ratio）是理赔费用与赔款之比，其中理赔费用包括直接理赔费用和间接理赔费用。注意，理赔费用率的分母是赔款，而不是保费，因此，赔款和理赔费用率不等于赔付率和理赔费用率之和，而等于赔付率乘以（1+理赔费用率），即赔款和理赔费用率=赔付率×（1+理赔费用率）
       承保费用率（underwriting expense ratio）是每单位保费中用于支付承保费用的部分，可以用承保费用和保费之比进行估计。保险公司通常将承保费用分解为两部分，一部分是在保单签发时发生的承保费用（如代理人佣金、广告费用和保费税等），另一部分是在整个保险期间发生的承保费用（如一般管理费用）。为了满足配比原则，在计算承保费用率时，第一部分承保费用通常与承保保费相比，而第二部分承保费用与已赚保费相比。将这两部分比值相加就可以得到承保费用率的估计值。通过这个比率，保险公司可以监控承保费用的变化情况，并且与其他保险公司进行对比。
       经营费用率（operational expense ratio）是每单位保费中用于支付理赔费用和承保费用的部分，等于承保费用率加上理赔费用与已赚保费之比，即经营费用率=承保费用率+理赔费用÷已赚保费
       经营费用率可以用于监控公司的经营费用及其变化情况，是决定保险公司总体利润水平的关键因素之一。
       综合成本率（combined ratio）是赔款率和费用率之和，是衡量保险业务利润水平的主要指标，传统上用下述公式计算： $=赔付率+\frac{理赔费用}{已赚保费}+\frac{承保费用}{承保保费}$
       在计算综合成本率时，赔付率中不能包含理赔费用，否则会造成重复计算。
       在计算承保费用率时，有些保险公司会在分母上使用已赚保费，此时，可以如下计算综合成本率：综合成本率=赔付率+经营费用率
       在非寿险费率厘定和经营管理中常用的另外两个比率指标是续保率和签约率。续保率（renew ratio）是指现有被保险人在保单到期时续保的比率，其计算公式为： $=\frac{实际的续保保单数}{潜在的可续保保单数}$
       譬如，保险公司在某月有 100 万份保单到期，从而可以进行续保，结果只有 80 万份保
单进行了续保，则当月的续保率就是 80%。续保率的定义在不同公司之间可能存在较大差别，譬如，有些公司在计算续保率时可能会剔除因为被保险人死亡而没有续保的保单，而另一些公司可能并不剔除这类保单。
       续保率可以反映当前费率水平的市场竞争力，也可以用于预测未来的业务规模。
       签约率（close ratio，conversion rate）是指在收到保险公司报价的潜在投保人中实际上与公司签订保险合同的比率，其计算公式如下： $=\frac{实际签订合同的人数}{收到公司报价的人数}$
       譬如，在某月有 100 万人收到了保险公司的报价，结果有 50 万人签订了保险合同，则
签约率就为 50%。与续保率一样，签约率在不同公司之间的定义也可能是不同的。譬如，如果同一个人收到了多次报价，则有些公司可能会作为一次报价计算签约率，而有些公司可能会作为多次报价计算签约率。
       签约率可以反映新费率的市场竞争力。

五、计算总平均费率的调整幅度

5.1实操

下面用赔付率法计算总平均费率的调整幅度。利用2005-2007年的经验数据进行计算，可知总平均费用需要调整12.78%。具体计算过程如下表14所示。需要注意的是，在对经验期的赔款数据进行趋势化处理时，趋势期是从经验期的中点到新费率生效后的事故发生时间的中点。在该例子中，新费率从2008年7月1日开始生效，有效期为1年，所以事故发生期的中点为2009年7月1日。
在这里插入图片描述

5.2理论补充

5.2.1总平均费率的厘定

在获得经验期的风险单位数、保费、赔款和费用等数据并进行调整以后，就可以厘定总平均费率，即平均每个风险单位的保费水平。总平均费率的厘定可以采取两种基本方法，即纯保费法和赔付率法。下面分别对这两种方法进行简要介绍，并分析它们各自的特点。

5.2.1.1纯保费法

       纯保费是赔款和理赔费用之和。纯保费法（pure premium method）通过在纯保费上附加各种必要的费用和利润得到保费，因此，用纯保费法厘定的保费不仅能够满足预期的赔款和费用支出，而且能够提供预期的利润。
       纯保费法的费率厘定公式可以通过下述的基本保险方程（fundamental insurance equation）推导而来，即保费 = 赔款 + 理赔费用 + 承保费用 + 承保利润附加
       其中承保费用具体包括下述四类：
       （1）佣金和经纪人手续费
       （2）税金和保险保障基金等（下面简称为保费税）
       （3）其他展业费用
       （4）一般管理费用
       在费率厘定中，上述各类承保费用又可进一步划分为固定费用和变动费用两大类。固定费用与保费的高低相互独立，对于每个风险单位或每份保单而言是一个常数；变动费用随着保费的变化而变化，与保费成比例。
       若令：
        $R$ 表示每个风险单位的保费（即费率）；
        $P$ 表示每个风险单位的纯保费，即赔款和直接理赔费用之和；
        $F$ 表示每个风险单位的固定费用；
        $V$ 表示变动费用率，即单位保费中用于支付变动费用的比率；
        $Q$ 表示单位保费中的利润附加比率；
        $则上述保险方程可以表示为：$
        $R = P + (F + R V) + R Q$
       对上述公式进行变形，即可得到下述的保费计算公式：
        $\frac{P +F}{1-V-Q}$

5.2.1.2赔付率法

       赔付率法（loss ratio method）首先根据赔付率计算费率调整因子，然后对当前的费率进行调整得到新的费率。在赔付率法中，新费率等于费率调整因子与当前费率的乘积，用公式可以表示为
        $R=AR_0$
       其中 $R$ 表示未来的新费率， $R_0$ 表示当前的费率， $A$ 表示费率调整因子。
       由此可见，在赔付率法中，关键在于计算费率调整因子。费率调整因子可以用公式表示如下：
        $)=\frac{赔款和理赔费用率+固定费用率}{1-变动费用率-利润附加率}$
       其中赔款和理赔费用率（loss & LAE ratio）是单位保费中用于支付赔款和理赔费用的比率；固定费用率（fixed expense ratio）是单位保费中用于支付固定费用的比率。
       在费率调整因子的计算公式中，分子上是单位保费中需要用于支付赔款、理赔费用和固定费用的金额，而分母上是从单位保费中扣除变动费用和利润附加之后，理论上可以用于支付赔款、理赔费用和固定费用的金额。如果分子和分母相等，说明在当前费率水平下，实际需要的金额和可以使用的金额相等，因此费率水平无需调整，反之，就需要对当前的费率水平进行调整。
       上述费率调整因子可以通过基本保险方程求得。将前述的基本保险方程变形，当前费率水平下的利润附加比率可以表示为：
        $Q_0=1-\frac{P+F}{R_0}-V$
       费率厘定的最终目标是确保公司目标利润的实现。在这里具体表现为利润附加比率应
该达到目标水平。如果当前费率水平下的利润附加比率低于（或高于）目标水平，就应该相应地提高（或降低）当前费率，即将其乘上一个费率调整因子。换言之，如果用 $Q$ 表示目标利润附加比率，则应有
        $Q=1-\frac{P+F}{A×R_0}-V$
       上式经变形，即可求得实现目标利润附加的费率调整因子为：
        $A=\frac{P/R_0+F/R_0}{1-V-Q}$
       在上式中，分子上的第一项是经验期的赔付率（loss ratio），即经验期的赔款和理赔费用在保费中所占的比率；第二项是固定费用率（fixed expense ratio），即固定费用在保费中所占比率。分母上也被称作可变允许赔付率（variable permissible loss ratio）。上式中各个项目都可以根据调整以后的经验数据计算求得。

5.2.1.3纯保费法与赔付率法的比较

       前面我们介绍了厘定总平均费率的两种方法，即纯保费法和赔付率法。从实际应用的角度看，这两种方法是不同的，但从理论上讲，赔付率法只是纯保费法的另一种表现形式，它们在本质上是等价的，只是所需数据不同而已。
       如果所有数据都是已知的，则上述两种计算方法会得出完全相同的结果。事实上，在赔付率方法中，用费率调整因子乘以当前费率，即可得到纯保费法中的费率计算公式。但在实际应用中，由于可获得的数据会受到一定限制，因此需要注意它们的不同特点：
       第一、纯保费法基于每个风险单位的纯保费（赔款和理赔费用）计算保费，因此，如果风险单位的确定比较困难或者风险单位在不同个体风险之间难以保持一致（如商业火灾保险），就不宜使用纯保费法。
       第二、应用赔付率法需要已知当前的费率水平，因此赔付率法不适用于新业务的费率厘定。对于新业务，最好在预测期望赔款（纯保费）的基础上，应用纯保费法厘定其保费。
       第三、应用赔付率法需要计算经验赔付率，而经验赔付率是经验期的赔款和当前费率水平下的已赚保费之比。因此，如果该险种在经验期的费率变化较大，计算当前费率水平下的已赚保费很困难时，最好使用纯保费法。譬如，在个人汽车保险中，保险公司通常使用奖惩系统，即根据保单持有人的索赔经验调整其续期保费，而且使用的费率因子较多，这就使得计算当前费率水平下的已赚保费比较困难。但是，汽车保险的风险单位数比较容易确定，因此采用纯保费法厘定费率更为方便。

六、计算各个风险类别的趋势化最终赔款

6.1 实操

应用赔款的进展因子和趋势因子，计算经验期内各个风险类别的趋势化最终赔款（见下表15）
在这里插入图片描述

七、计算各个风险类别的平均相对费率

7.1 实操

用各个风险类别的趋势化最终赔款除以已赚风险单位数，可以得到各个风险类别的趋势化纯保费。将每个风险类别的纯保费与基础类别的纯保费相比，即得到该风险类别纯保费的一个相对费率估计值。计算过程如下表16所示。在表16中，分别以驾驶员类型1和行驶区域2为基础类别。
在这里插入图片描述

八、计算各个风险类别的加权平均相对费率

8.1 实操

8.1.1 计算驾驶员类型的加权平均相对费率

首先用已赚风险单位对上一步的计算结果进行加权平均，分别得到驾驶员类型2、3对驾驶员类型1的相对费率。然后，如果考虑到各个风险类别的风险单位数较小，还需要进行信度调整。计算过程如表17所示。
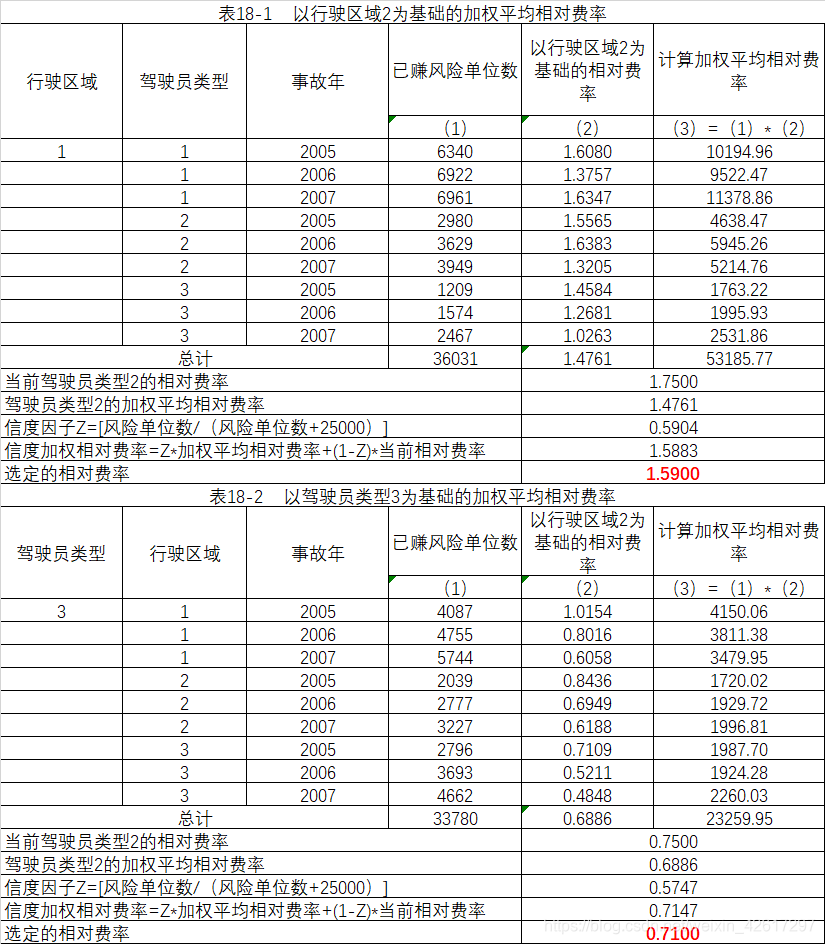
在这里插入图片描述

8.1.2 计算行驶区域的加权平均相对费率

与驾驶员类型的相对费率的计算过程相似，行驶区域的相对费率的计算过程如表18所示。
在这里插入图片描述

九、进行平衡调整

9.1 实操

由于相对费率的调整也会造成总平均费率水平的变化，所以必须对基础类别（驾驶员类型1和行驶区域2）的费率进行平衡调整，使得总平均费率的调整幅度正好等于前述的计算结果，即保持为12.78%。计算过程如表19所示。从表19可以看出，相对费率的调整会使总平均费率水平下降9.18%，为了确保总平均费率水平的上调幅度保持在12.78%，应该将基础类别的费率水平上调24.18%。
在这里插入图片描述

十、计算各个风险类别的新费率

10.1 实操

将基础风险类别的费率乘以驾驶员类型的相对费率和行驶区域的相对费率，即可得到各个风险类别的新费率。将新费率乘以2007年的风险单位数，即可得到在新的费率水平下2007年的保费收入，由此可以验证新费率使得总平均费率水平上升了12.78%。各个风险类别的新费率如表20所示。
在这里插入图片描述

十一、计算赔偿限额为100/300的増限因子

11.1 实操

如果可以通过趋势化方法求得新费率使用期的无赔款限额、基本赔款限额和增长限额三种情况下的赔款金额分布，就可以计算出相应的増限因子。假设已经求得了趋势化至2007年12月31日的赔款分布如表21所示，由此可以求得2007年12月31日时限额为100/300的増限因子为1.2919。如果进一步假设2005年12月31日时求得的限额为100/300的増限因子是1.2184，则可以得到増限因子的增长趋势为2.97%。其他计算过程和计算结果如表21所示。
在这里插入图片描述

十二、新费率表

12.1 实操

通过以上12步的计算，我们得到了2008年7月1日生效的新费率和増限因子如表22和表23所示。
在这里插入图片描述

12.2 理论补充

12.2.1 费率厘定的基本原则

       费率厘定是基于历史经验数据对未来期望赔款和费用的前瞻性预测。为了确保费率厘定结果的合理性，精算师在费率厘定过程中必须遵循一些基本原则。CAS（Casualty Actuarial Society）将费率厘定的 4 个基本原则表述如下：
       原则一：费率是对未来期望保险成本的一个估计值。
       原则二：费率应该能够补偿风险转移的所有成本。
       原则三：费率应该能够补偿个体风险转移的所有成本。
       原则四：费率应当是充足的、不过高、且没有不公平的区别对待。
       费率厘定的第一个原则表明费率厘定过程是一种前瞻性预测。第二个原则要求保险公司收取的保费应该能够补偿其成本和费用支出，确保公司运营的财务安全。第三个原则要求每个被保险人的保费应该等于其期望赔款和费用支出，从而确保不同被保险人的保费负担是公平的。如果费率厘定过程满足了上述三个原则，则必然是充足的、不过高、且没有不公平的区别对待。
       在非寿险费率厘定过程中，精算师不仅需要遵循上述四个基本原则，同时还需要考虑各种因素。根据 CAS关于费率厘定原则的有关文件，精算师在费率厘定过程中应该考虑下述因素：
       （1） 风险单位。风险单位是度量风险和计算保费的基础，因此必须慎重选择，确保风险单位能够反映风险的大小，并且可以客观度量，便于操作。
       （2）数据。历史经验期的保费、风险单位数、赔款和费用等数据是厘定费率的起点，其他相关数据可以作为补充。其他相关数据可以是公司外部的数据，也可以是保险业外部的数据，这些数据可以反映索赔频率、索赔强度、费用和保费的变动趋势。
       （3） 数据汇总。有多种方法可以对数据进行汇总，包括日历年度法、事故年度法、保单年度法和报案年度法等。这些方法各有优缺点，但如果应用得当，每种方法都可用于费率厘定。在选择数据的汇总方法时，需要考虑数据的可获得性、方法的简单易行性、以及保险产品的特点等。
       （4） 风险的同质性。在很多情况下，将风险细分成具有相似风险特征的风险类别可以提高费率厘定结果的准确性。
       （5） 经验数据的可信度。经验数据的可信度随着数据同质性的增加或数据规模的增加而增加。一般而言，风险分类越细致，经验数据的同质性就越好，但每个类别的数据规模就越小，因此精算师必须平衡好同质性和数据规模之间的关系。
       （6） 损失进展。由于报案延迟和理赔延迟的影响，精算师在定价时获得的数据通常不是最终赔款数据，因此需要采取适当的方法进行预测，也就是把已报案赔款进展到最终赔款。
       （7） 趋势调整。费率厘定是基于历史经验数据对未来的期望赔款和费用进行预测，因此必须考虑经验期与未来新费率使用期之间在保障范围、索赔频率、索赔强度、风险单位数、费用和保费等方面的差异。
       （8）巨灾。费率厘定时必须考虑巨灾对经验数据的影响，并采取适当的方法在保费中附加巨灾损失。
       （9） 保单条款。在费率厘定时应当考虑残值、代位追偿、共保、赔偿限额、免赔额和其他保单条款的影响。
       （10） 业务结构。费率厘定时应当考虑公司承保的业务在免赔额、赔偿限额和风险类型等方面的分布变化情况，这些变化有可能影响索赔频率或索赔强度。
       （11） 再保险。费率厘定时应当考虑再保险安排所产生的影响。
       （12） 公司经营行为的变化。在费率厘定时精算师还必须考虑公司在承保、理赔、逐案估损准备金评估和市场营销等方面的变化，这些变化会影响经验数据的连续性和一致性。
       （13） 其他影响因素。影响费率厘定的其他因素包括法律法规和宏观经济变量等。
       （14） 风险分类计划。一个合理的风险分类计划可以提高费率厘定结果的准确性。
       （15） 个体风险的费率厘定计划。当个体风险的经验数据具有足够的可信度时，就应该根据个体风险的损失经验对其手册费率进行调整。在费率厘定时，精算师应该考虑个体风险的费率厘定计划对总体经验数据的影响。
       （16） 风险附加和承保利润附加。保费除了支付未来的期望赔款和费用之外，还应该注意到保险公司的实际赔款有可能偏离其期望值，因此在费率厘定中应该考虑对保险公司承担这部分随机风险的补偿。这部分补偿通常在确定公司的总体收益目标时予以考虑，而公司的总体收益目标取决于资本金的成本。此外，如果赔款成本的估计值系统地偏离了期望赔款，还应该在费率厘定中考虑不利偏差准备（contingency provision）。
       （17） 投资收益和其他收益。在费率厘定中应该考虑公司可能获得的投资收益和其他收益。
       （18） 精算判断。在费率厘定过程中的各个环节，精算师都可以合理运用自己的专业判断，但在精算报告中应该予以披露。

附录

1.Python代码实操

准备

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import pandas as pd

数据导入

dt_0 = pd.read_excel('data.xlsx', sheet_name=2)
dt_development = pd.read_excel('data.xlsx', sheet_name=3)# 导入已发生赔款与直接理赔费用、已报告索赔数的流量表

计算已赚保费

dt_0['Premium'] = dt_0['EarnExposures'] * dt_0['Rating']

# 按照事故年以及驾驶区域汇总已赚风险单位数、已赚保费
dt_0_AccidentYear_DrivingArea = dt_0[['AccidentYear','DrivingArea','EarnExposures','Premium']].groupby(['AccidentYear','DrivingArea']).sum()
dt_0_AccidentYear_DrivingArea.reset_index()

# 按照事故年以及驾驶员类型汇总已赚风险单位数、已赚保费
dt_0_AccidentYear_DriverType = dt_0[['AccidentYear','DriverType','EarnExposures','Premium']].groupby(['AccidentYear','DriverType']).sum()
dt_0_AccidentYear_DriverType.reset_index()

# 按照事故年汇总已赚风险单位数、已赚保费
dt_0_AccidentYear = dt_0[['AccidentYear','EarnExposures','Premium']].groupby(['AccidentYear']).sum()
dt_0_AccidentYear.reset_index()

计算进展因子

num1 = dt_development.time.unique().tolist()  # 统计进展年
num2 = dt_development[dt_development.time ==num1[0]].IncurredLossAlae.count()  # 统计事故年个数

# 使用简单算术平均方法计算进展因子
ILAD =[]  # 保存已发生赔款与直接理赔费用的进展因子
CFD = []  # 保存已报告索赔数的进展因子
for i in range(len(num1)-1):
    num2 -= 1
    d_1 = dt_development[dt_development.time ==num1[i+1]].IncurredLossAlae[:num2].reset_index().IncurredLossAlae / dt_development[dt_development.time ==num1[i]].IncurredLossAlae[:num2].reset_index().IncurredLossAlae
    d_2 = dt_development[dt_development.time ==num1[i+1]].ClaimF[:num2].reset_index().ClaimF / dt_development[dt_development.time ==num1[i]].ClaimF[:num2].reset_index().ClaimF
    ILAD.append(d_1.mean())
    CFD.append(d_2.mean())
ILAD = ILAD+[1]  # 增加尾部进展因子
CFD = CFD+[1]
ILAD = ILAD[::-1] # 逆序
CFD = CFD[::-1]

ILADCum = [1] #表示已发生赔款与直接理赔费用尾部进展因子。用于计算累计进展因子
CFDCum = [1] #表示已报告索赔数尾部进展因子
for i in range(len(ILAD)-1):
    x_1 = ILADCum[i] * ILAD[i+1]
    x_2 = CFDCum[i] * CFD[i+1]
    ILADCum.append(x_1)
    CFDCum.append(x_2)
ILADCum,CFDCum

计算终极赔款以及索赔次数

num3 = dt_development.AccidentYear.unique().tolist() # 统计事故年
IncurredLossAlaeNew = []  # 统计截止目前每年事故年的已发生赔款与直接理赔费用
ClaimFNew = []  # 统计截止目前每年事故年的已报告索赔数
for i in range(len(num3)):
    xx_1 = dt_development[dt_development.AccidentYear == num3[i]].IncurredLossAlae.max()
    xx_2 = dt_development[dt_development.AccidentYear == num3[i]].ClaimF.max()
    IncurredLossAlaeNew.append(xx_1)
    ClaimFNew.append(xx_2)
IncurredLossAlaeNew,ClaimFNew

计算索赔强度以及索赔频率

# 预测各事故年的最终已发生赔款与直接理赔费用、最终已报案索赔数
lt = dt_0_AccidentYear.EarnExposures.tolist()[::-1]
lt.extend([34770,30529,26790])  # 增加从2002-2004年的经验数据
lt = lt[::-1]
dt_development_2 = {'AccidentYear':num3,
        'time':num1,
       'IncurredLossAlaeNew':IncurredLossAlaeNew,
       'ILADCum':ILADCum,
       'ClaimFNew':ClaimFNew,
       'CFDCum':CFDCum,
        'EarnExposures':lt}
dt_development_2 = pd.DataFrame(dt_development_2)
dt_development_2['IncurredLossAlaeLast'] = dt_development_2.IncurredLossAlaeNew * dt_development_2.ILADCum  # 最终赔款与直接理赔费用的预测值
dt_development_2['ClaimFLast'] = dt_development_2.ClaimFNew * dt_development_2.CFDCum  # 最终索赔次数的预测值
dt_development_2['time2'] = dt_development_2.time + 1
dt_development_2['ClaimSeverity'] = dt_development_2.IncurredLossAlaeLast / dt_development_2.ClaimFLast  # 最终索赔强度的预测值
dt_development_2['ClaimFreq'] = dt_development_2.ClaimFLast / dt_development_2.EarnExposures  # 最终索赔频率的预测值

计算索赔强度的年度增长趋势因子

from sklearn.linear_model import LinearRegression

# 采用线性模型得到索赔强度的年度增长趋势因子
Y_1  = dt_development_2[['ClaimSeverity']]
X_1 = dt_development_2[['time']]
model_1 = LinearRegression()
model_1.fit(X_1,Y_1)
model_1.coef_,model_1.intercept_  # 斜率、截距
Y_predict_1 = model_1.predict(X_1)  # 最终索赔强度的拟合值
CSTF = Y_predict_1[-1] / Y_predict_1[-2]  #索赔强度的年度增长趋势因子

计算索赔频率的年度增长趋势因子

# 采用指数模型得到索赔频率的年度增长趋势因子
import numpy as np
Y_2  = dt_development_2[['ClaimFreq']].apply(lambda x:np.log(x))
X_2 = dt_development_2[['time2']]
model_2 = LinearRegression()
model_2.fit(X_2,Y_2)
model_2.coef_,model_2.intercept_  # 斜率、截距
CFTF = np.exp(model_2.coef_)  #索赔频率的年度增长趋势因子

计算目标赔付率

# 计算目标赔付率
V1 = 20 / 100   #佣金（占保费的百分比）
V2 = 2.5/ 100  #税金（占保费的百分比）
V3 = 5.9/ 100   #其他展业费用（占保费的百分比）
V4 = 6.8/ 100   #一般管理费用（占保费的百分比）
V = V1 + V2 + V3 + V4   #费用率（占保费的百分比）
Q = 0  #假设利润率
G =  7.02/ 100  #间接理赔费用率（占赔款和直接理赔费用的百分比）
T = (1 - V -Q) / (1 + G)   #目标赔付率

计算总平均费率的调整幅度

# 计算总平均费率的调整幅度
dt_development_3 = {'AccidentYear':num3[-3:], # 事故年
                    'IncurredLossAlaeLast':dt_development_2.IncurredLossAlaeLast.tolist()[-3:], # 赔款与直接理赔费用的预测值
                    'Premium':dt_0_AccidentYear.Premium.tolist(), # 当前费率水平下的已赚保费
                   'trendtime':[4,3,2], # 趋势期限
                    'ILADCum':ILADCum[-3:] # 最终累计进展因子
                   }
dt_development_3 = pd.DataFrame(dt_development_3)
dt_development_3['ClaimSeverity'] = dt_development_3['trendtime'].apply(lambda x:np.power(CSTF,x)[0])  # 索赔强度
dt_development_3['ClaimFreq'] = dt_development_3['trendtime'].apply(lambda x:np.power(CFTF,x)[0][0])  # 索赔频率
dt_development_3['ClaimSeverityTrend'] = dt_development_3['IncurredLossAlaeLast'] *  dt_development_3['ClaimSeverity'] * dt_development_3['ClaimFreq']# 趋势化赔款和直接理赔费用
dt_development_3['LossRatioTrend'] = dt_development_3['ClaimSeverityTrend'] / dt_development_3['Premium']
LRT = dt_development_3['ClaimSeverityTrend'].sum() / dt_development_3['Premium'].sum() 
RA = LRT / T -1 # 总平均费率的调整幅度

计算各个风险类别的趋势化最终赔款

# 计算各个风险类别的趋势化最终赔款
dt_development_4 = dt_development_3[['AccidentYear','ClaimSeverity','ClaimFreq','ILADCum']]
dt_1 = pd.merge(dt_0, dt_development_4, how='left', on=['AccidentYear'])
dt_1['IncurredLossAlaeLastTrend'] = dt_1['IncurredLossAlae'] * dt_1['ILADCum'] * dt_1['ClaimSeverity'] *dt_1['ClaimFreq'] # 趋势化的最终赔款 与直接理赔费用

计算各个风险类别的相对费率

# 计算各个风险类别的相对费率
dt_1['PremiumTrend'] = dt_1['IncurredLossAlaeLastTrend'] / dt_1['EarnExposures']  # 计算趋势化纯保费

# 驾驶员类型1、行驶区域2为基础类别
# 计算驾驶员类型的相对费率
dt_DriverType = dt_1[dt_1.DriverType == 1][['DrivingArea','DriverType','AccidentYear','PremiumTrend']]
dt_2 = pd.merge(dt_1, dt_DriverType, how='left', on=['DrivingArea','AccidentYear'])
dt_2['PremiumTrendDriverType'] = dt_2['PremiumTrend_x'] / dt_2['PremiumTrend_y']
# 计算行驶区域的相对费率
dt_DrivingArea = dt_2[dt_2.DrivingArea == 2][['DrivingArea','DriverType_x','AccidentYear','PremiumTrend_x']]
dt_2 = pd.merge(dt_2, dt_DrivingArea, how='left', on=['DriverType_x','AccidentYear'])
dt_2['PremiumTrendDrivingArea'] = dt_2['PremiumTrend_x_x'] / dt_2['PremiumTrend_x_y']

dt_2 = dt_2.drop(['DriverType_y','PremiumTrend_y','DrivingArea_y','PremiumTrend_x_y'],axis=1)
dt_2.rename(columns={'DrivingArea_x':'DrivingArea','DriverType_x':'DriverType','PremiumTrend_x_x':'PremiumTrend'}, inplace=True)

计算以驾驶员类型1为基础的加权平均相对费率

# 计算以驾驶员类型1为基础的加权平均相对费率
# 计算驾驶员类型2的加权平均相对费率
dt_2_DriverType2 = dt_2[dt_2.DriverType == 2]
dt_2_DriverType2['PremiumTrendDriverTypeW'] = dt_2_DriverType2['EarnExposures'] * dt_2_DriverType2['PremiumTrendDriverType']
DriverType2R = dt_2_DriverType2.PremiumTrendDriverTypeW.sum() / dt_2_DriverType2.EarnExposures.sum()  # 驾驶员类型2的加权相对费率
DriverType2C = dt_2[dt_2.DriverType == 2].Rating.sum() / dt_2[dt_2.DriverType == 1].Rating.sum() # 当前驾驶员类型2的相对费率
DriverType2CF = (dt_2_DriverType2.EarnExposures.sum() / (dt_2_DriverType2.EarnExposures.sum() + 25000))  # 信度因子
DriverType2W = DriverType2CF * DriverType2R + (1-DriverType2CF ) * DriverType2C # 信度加权相对费率

# 计算驾驶员类型3的加权平均相对费率
dt_2_DriverType3 = dt_2[dt_2.DriverType == 3]
dt_2_DriverType3['PremiumTrendDriverTypeW'] = dt_2_DriverType3['EarnExposures'] * dt_2_DriverType3['PremiumTrendDriverType']
DriverType3R = dt_2_DriverType3.PremiumTrendDriverTypeW.sum() / dt_2_DriverType3.EarnExposures.sum()  # 驾驶员类型2的加权相对费率
DriverType3C = dt_2[dt_2.DriverType == 3].Rating.sum() / dt_2[dt_2.DriverType == 1].Rating.sum() # 当前驾驶员类型2的相对费率
DriverType3CF = (dt_2_DriverType3.EarnExposures.sum() / (dt_2_DriverType3.EarnExposures.sum() + 25000))  # 信度因子
DriverType3W = DriverType3CF * DriverType3R + (1-DriverType3CF ) * DriverType3C # 信度加权相对费率


# 计算以行驶区域2为基础的加权平均相对费率
# 计算行驶区域1的加权平均相对费率
dt_2_DrivingArea1 = dt_2[dt_2.DrivingArea == 1]
dt_2_DrivingArea1['PremiumTrendDrivingAreaW'] = dt_2_DrivingArea1['EarnExposures'] * dt_2_DrivingArea1['PremiumTrendDrivingArea']
DrivingArea1R = dt_2_DrivingArea1.PremiumTrendDrivingAreaW.sum() / dt_2_DrivingArea1.EarnExposures.sum()  # 驾驶员类型2的加权相对费率
DrivingArea1C = dt_2[dt_2.DrivingArea == 1].Rating.sum() / dt_2[dt_2.DrivingArea == 2].Rating.sum() # 当前驾驶员类型2的相对费率
DrivingArea1CF = (dt_2_DrivingArea1.EarnExposures.sum() / (dt_2_DrivingArea1.EarnExposures.sum() + 25000))  # 信度因子
DrivingArea1W = DrivingArea1CF * DrivingArea1R + (1-DrivingArea1CF ) * DrivingArea1C # 信度加权相对费率

# 计算行驶区域3的加权平均相对费率
dt_2_DrivingArea3 = dt_2[dt_2.DrivingArea == 3]
dt_2_DrivingArea3['PremiumTrendDrivingAreaW'] = dt_2_DrivingArea3['EarnExposures'] * dt_2_DrivingArea3['PremiumTrendDrivingArea']
DrivingArea3R = dt_2_DrivingArea3.PremiumTrendDrivingAreaW.sum() / dt_2_DrivingArea3.EarnExposures.sum()  # 驾驶员类型2的加权相对费率
DrivingArea3C = dt_2[dt_2.DrivingArea == 3].Rating.sum() / dt_2[dt_2.DrivingArea == 2].Rating.sum() # 当前驾驶员类型2的相对费率
DrivingArea3CF = (dt_2_DrivingArea3.EarnExposures.sum() / (dt_2_DrivingArea3.EarnExposures.sum() + 25000))  # 信度因子
DrivingArea3W = DrivingArea3CF * DrivingArea3R + (1-DrivingArea3CF ) * DrivingArea3C # 信度加权相对费率

DriverType2W,DriverType3W,DrivingArea1W,DrivingArea3W

根据上面DriverType2W,DriverType3W,DrivingArea1W,DrivingArea3W的计算结果来选定相对费率

# 根据上面DriverType2W,DriverType3W,DrivingArea1W,DrivingArea3W的计算结果来选定
DriverType2S = 1.27  # 驾驶员类型2选定的相对费率
DriverType3S = 1.58  # 驾驶员类型3选定的相对费率
DrivingArea1S = 1.59  # 行驶区域1选定的相对费率
DrivingArea3S = 0.71  # 行驶区域3选定的相对费率

进行平衡调整

# 进行平衡调整
dt_2_2017 = dt_2[dt_2.AccidentYear == 2007][['DrivingArea','DriverType','AccidentYear','Premium']].reset_index().drop(['index'],axis=1)

dt_balance_2007 = {'DrivingArea':[1,1,1,2,2,2,3,3,3], # 行驶区域
                    'DriverType':[1,2,3,1,2,3,1,2,3], # 驾驶员类型
                    'DriverTypeC':[1,DriverType2C,DriverType3C,1,DriverType2C,DriverType3C,1,DriverType2C,DriverType3C], # 当前驾驶员类型的相对费率
                   'DrivingAreaC':[DrivingArea1C,DrivingArea1C,DrivingArea1C,1,1,1,DrivingArea3C,DrivingArea3C,DrivingArea3C], # 当前行驶区域的相对费率
                    'DriverTypeS':[1,DriverType2S,DriverType3S,1,DriverType2S,DriverType3S,1,DriverType2S,DriverType3S], # 驾驶员类型的选定相对费率
                   'DrivingAreaS':[DrivingArea1S,DrivingArea1S,DrivingArea1S,1,1,1,DrivingArea3S,DrivingArea3S,DrivingArea3S], # 当前行驶区域的相对费率
                   }
dt_balance_2007 = pd.DataFrame(dt_balance_2007)
dt_balance_2007 = pd.merge(dt_2_2017, dt_balance_2007, how='left', on=['DrivingArea','DriverType'])
dt_balance_2007['RatingC'] = dt_balance_2007.DriverTypeC * dt_balance_2007.DrivingAreaC  # 以驾驶员类型1和行驶区域2为基础类别的当前相对费率
dt_balance_2007['RatingS'] = dt_balance_2007.DriverTypeS * dt_balance_2007.DrivingAreaS # 对驾驶员类型1和行驶区域2选定的相对费率
dt_balance_2007['RatingRelativeChange'] = dt_balance_2007.RatingS / dt_balance_2007.RatingC - 1  # 相对费率的变化
dt_balance_2007['PremiumChange'] = dt_balance_2007.Premium * dt_balance_2007.RatingRelativeChange # 对保费的影响
RatingRelativeChange = dt_balance_2007.PremiumChange.sum() / dt_balance_2007.Premium.sum()   # 总平均费率的调整幅度
BasicRatingChange =  (1+RA)/(1+RatingRelativeChange) -1     # 基础类别的费率调整幅度
BasicRatingCurrent =  dt_0[(dt_0.DrivingArea == 2) & (dt_0.DriverType == 1)].Rating.mean() # 行驶区域2、驾驶员类型1的当前费率
BasicRatingNew = BasicRatingCurrent * (1+BasicRatingChange) # 行驶区域2、驾驶员类型1的新费率

计算各个风险类别的费率

# 计算各个风险类别的费率
dt_balance_2007['BasicRatingNew'] = BasicRatingNew
dt_balance_2007['RatingNew'] = dt_balance_2007.DriverTypeS *  dt_balance_2007.DrivingAreaS * dt_balance_2007.BasicRatingNew # 各个风险类别的费率
dt_balance_2007['RatingNew2'] = dt_balance_2007['RatingNew'].apply(lambda x: round(x))

得到新费率表

dt_balance_2007[['DrivingArea','DriverType','RatingNew2']]  # 得到新费率表

参考

[1] 中国精算师协会组编：非寿险定价[M]，中国财政经济出版社2011年版