手绘图系列 05 | 元素减半，快乐加倍的二叉搜索树

非科班大厂码农（同名公众号）

于 2024-08-10 15:57:22 发布

阅读量454

点赞数 18

分类专栏：数据结构与算法文章标签：算法

本文链接：https://blog.csdn.net/weixin_42627385/article/details/141092127

版权

数据结构与算法专栏收录该内容

7 篇文章 0 订阅

订阅专栏

手绘图手撕数据结构与算法系列目录：
手绘图系列 01 | 链表到底是什么？
手绘图系列 02 | 让人害怕的栈溢出
 手绘图系列 03 | 排队？还是不排队？
手绘图系列 04 | 使用频率最高的”树“

前面一篇文章，我们介绍了树这种数据结构：树本质上只是由许多相互连接的节点和边组成的。

树在我们的开发中到处可见，但最常见（也可以说是最强大）的就是二叉搜索树。

二叉搜索树，简称BST，是遵循一定规则的树。仅从它们的名字，你可能就能猜到这些规则是什么。正是这些特定的规则赋予了二叉搜索树强大的功能，并使其非常有用。在我们深入探讨二叉搜索树之前，让我们先详细了解一下它是什么，以及它与其他树结构的不同之处！

二叉树

在介绍二叉搜索树之前，我们先看看什么是二叉树。

二叉树的名字来源于其结构：二叉树中任何一个节点最多只有2个子节点，

我们知道树是递归的数据结构，这意味着一棵树是由许多子树组成的。

那么递归如何体现在二叉树中呢？由于二叉树的每个节点，只能有两个子节点，这意味着根节点也只能指向两个子树：一个左子树和一个右子树。而随着我们深入到树的底部，这条规则不断适用：左子树和右子树本身也是二叉树，因此，左子树的根节点也会指向两个子树，从而形成自己的左子树和右子树。

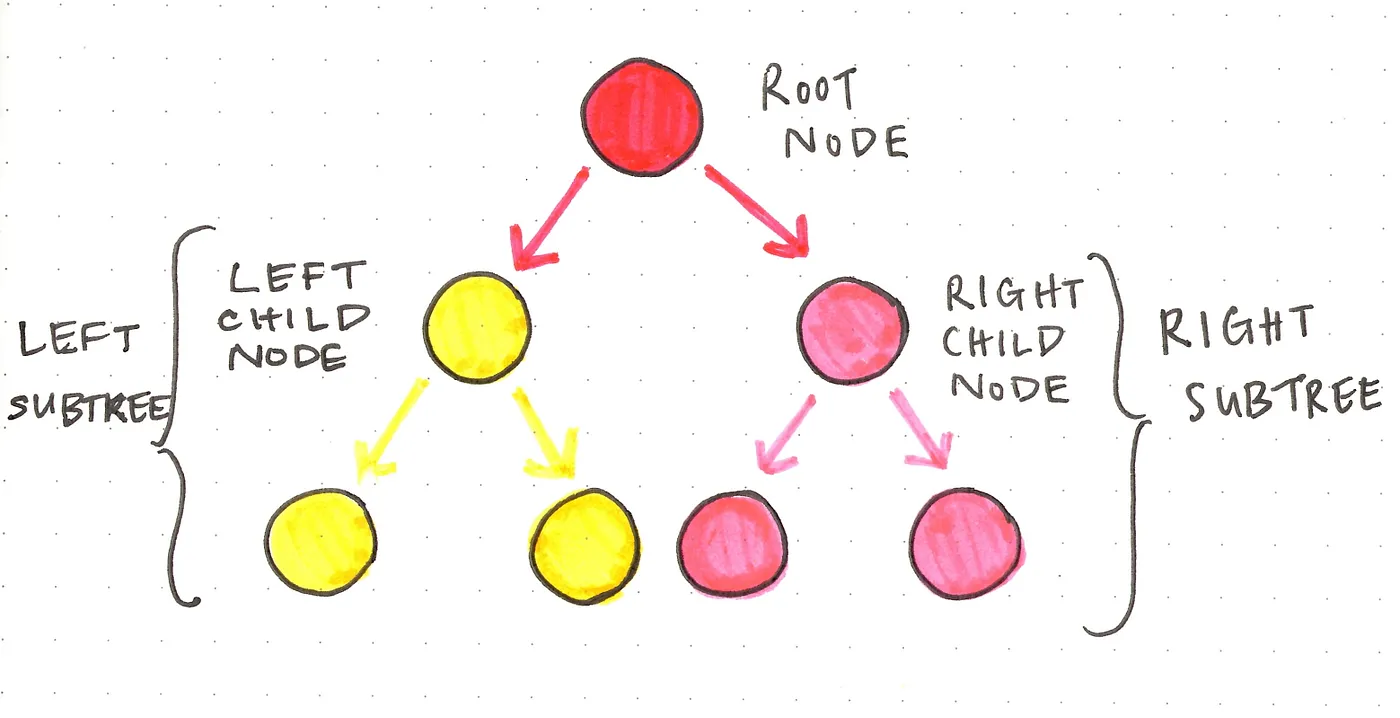
二叉搜索树（BST ）的排序规则

那么什么是二叉搜索树？为什么它会成为我们最常使用的一种树？

如果你还没有完全理解二叉搜索树的强大之处，那是因为我们还没有提到二叉搜索树的一个重要特征：二叉搜索树的节点必须按照特定的方式组织。事实上，正是二叉搜索树的组织和排序方式使其成为“可搜索”的。

对于一颗二叉搜索树，它会满足以下4个条件：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉搜索树；
没有键值相等的节点。

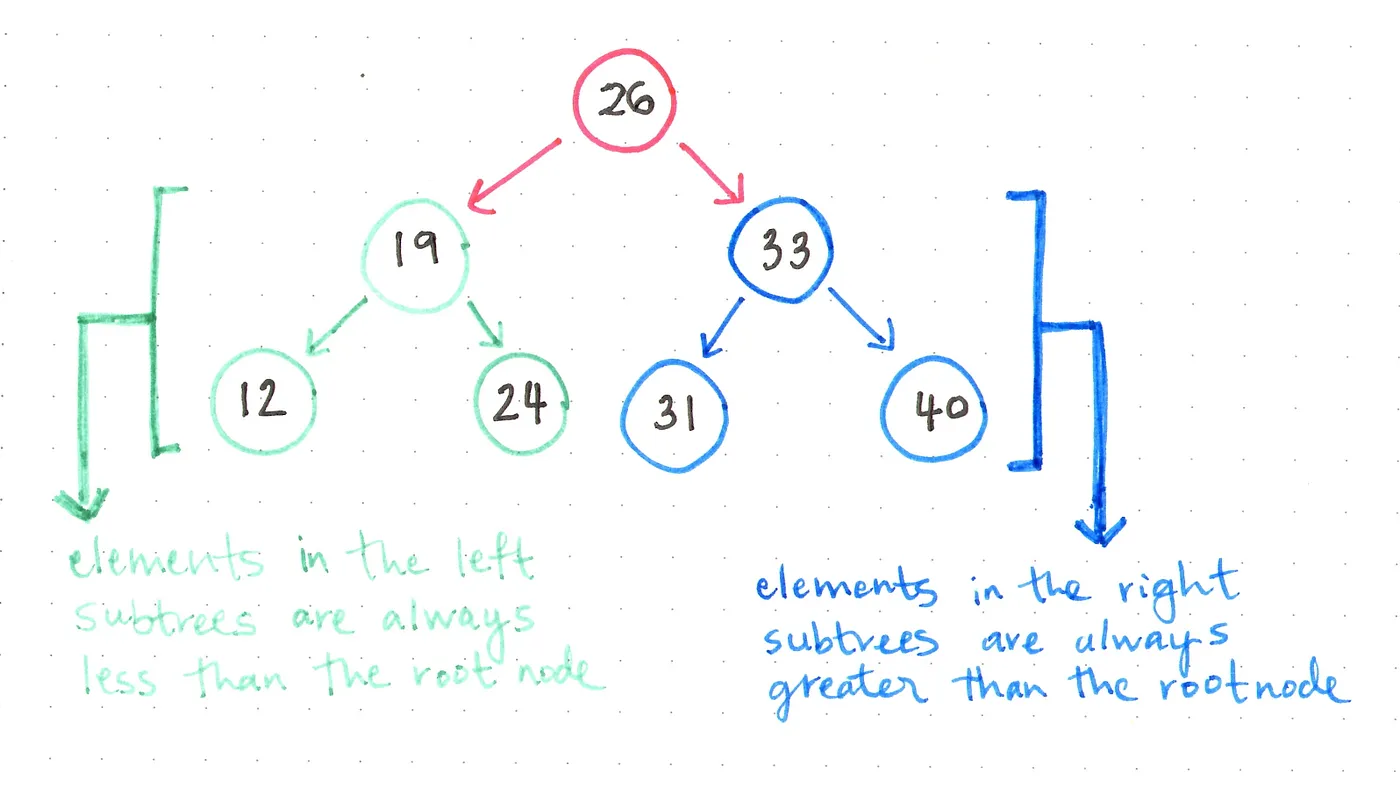
上图就是一颗二叉搜索树，根节点为26，其左侧的所有节点都小于26（满足条件1），其右侧的所有节点都大于26（满足条件2），如果我们进一步观察根节点左侧的绿色子树。这颗绿色子树的根节点是19，它左边的节点12小于19，右边节点24大于19，如果你有兴趣继续研究，会发现任意一颗子树都这样（满足条件3）。而且这颗树没有相同的两个节点（满足条件4）

节点的这种排序规则使得在二叉搜索树中查找指定元素变得非常高效。而且这种排序会影响我们在树上执行的其它操作。举例来说，假设我们想执行一个 insert() 操作，即将一个值插入到二叉搜索树中的正确位置。

以下图为例，我们准备再现有的二叉搜索树中添加一个新的元素 21。

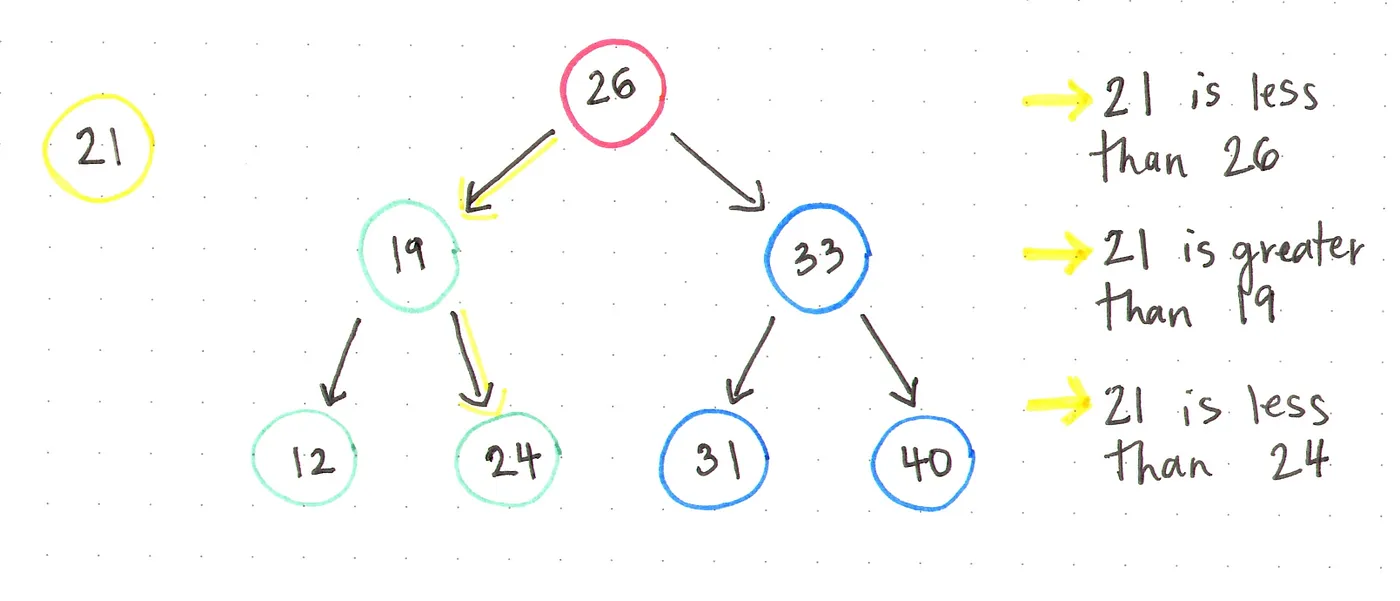
得益于二叉搜索树的排序规则，我们可以很容易地用伪代码编写一个insert()函数：

我们从根节点开始，并将其值26与我们要插入的值21进行比较。
由于21小于26，我们立即确定要插入的元素应该位于根节点的左子树中，因为根节点右子树的每个节点都要求比根节点26大。
接着，我们查看新的“根”节点，即19。我们知道21大于19，因此转向节点19的右侧子树。
现在我们来到节点24，大于我们要插入的21。而24又是整棵树的叶子节点了，因此我们将21插入到节点24的左侧。
我们将节点24的左指针引用指向要插入的节点21。插入完成！

二分查找：元素减半，效率加倍

二叉搜索树在计算机科学中非常特殊。其原因很简单：它们允许你利用二分查找算法的力量。你可能还记得，并非所有的二叉树都是二叉搜索树——它们必须以特定的方式组织，才能对它们执行二分查找。

等等——什么是二分查找？

二分查找是一种查找算法，我们不对其做过多定义，让我们通过绘图来理解！我们将使用之前的二叉搜索树，该树的根节点是26；不过为了便于理解，我们将其重新组织成数组，并且元素是按照从小到大排序的——二叉搜索树中序遍历可以得到有序的数组，什么是中序遍历，后面会详细介绍，在这里你只需要知道，我们有办法将二叉搜索树转换为有序数组就可以了。

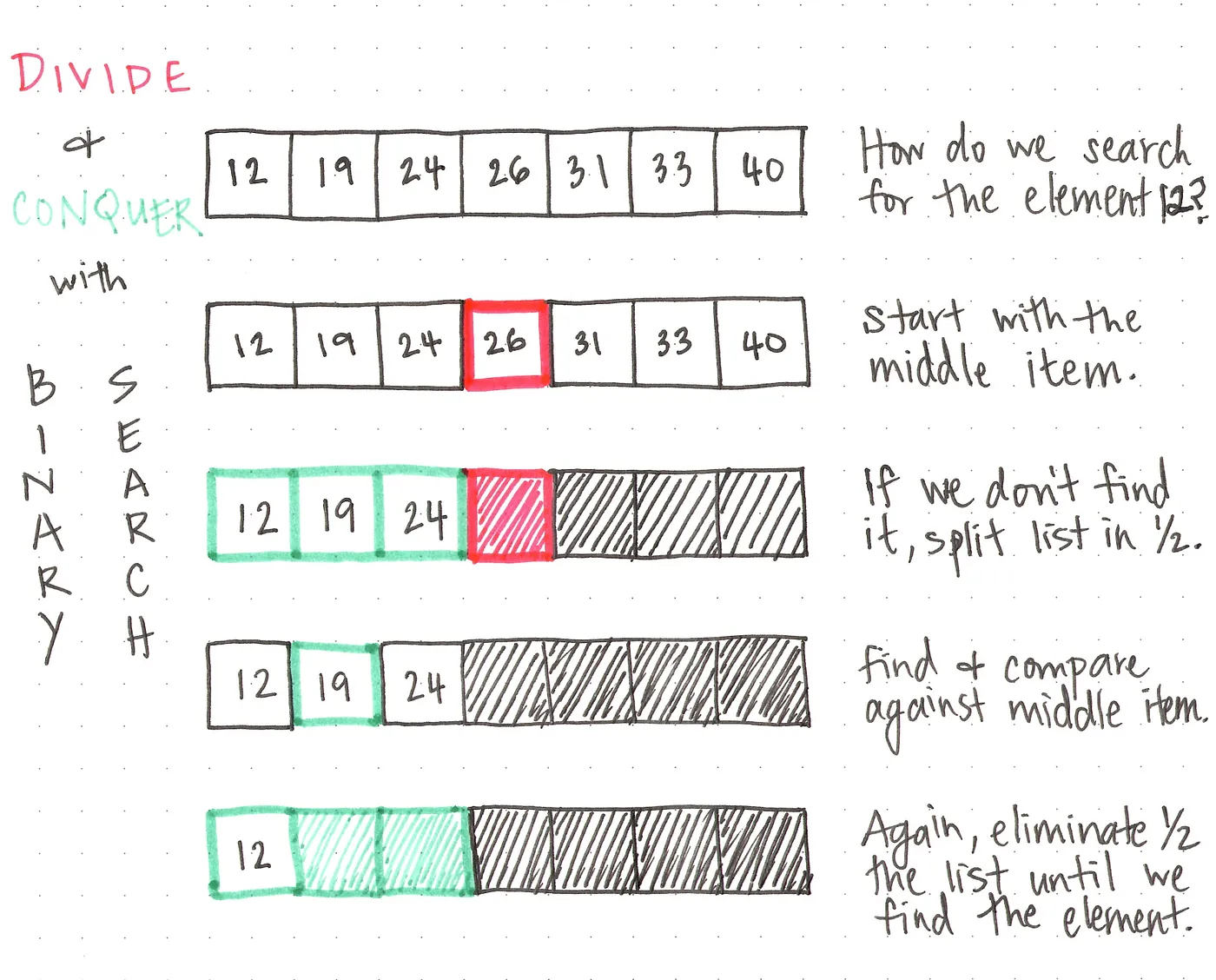
假设我们有7个元素（节点），我们要找的目标是12。现在的问题是，如何高效的找到值为12的节点呢？

我们知道这些元素是按大小排序的，所以可以利用这一点。我们从数组的中间元素开始，它是26。26比12大还是小？显然是更大。这意味着我们可以确定数组右侧的元素都不可能有12。因此，我们可以直接排除数组右侧的所有内容，即让下一次的查找减少了一半的工作量。

此时，我们只剩下3个元素需要查找。再看一下中间元素，它是19。19比12大还是小？显然也是更大。因此，我们可以再次排除这个元素右侧的所有内容，因为它们都太大了，不可能是我们要找的12，很好，工作量再次减少一半！

现在，剩下的唯一一个元素就是我们要找的12！很好，我们成功地找到了目标节点。

回顾这个过程，我们会发现，每次进行比较时，我们都排除了剩余元素中的一半。这种递减搜索规模的方式正是二分查找如此高效的原因。

通过上面这个例子，你应该可以开始理解这个名称的由来，以及为什么它如此贴切。我们可以搜索一个庞大的数据集，但通过每次比较将搜索空间减半，能够更加高效地找到目标。

最后一点也是最重要的：二分查找能够大大提高搜索效率，但是二分查找有一个前提：数据集是有序的,而二叉搜索树正好满足这个条件，因此在需要时可以对其执行二分查找。

日常中的二叉搜索树和二分查找

抽象概念在理解其应用场景后才能真正体现其价值。这引出了一个问题：二分查找和二叉搜索树究竟在计算机科学的哪些领域得到应用？

答案是：在很多地方！一个具体的例子是数据库。如果你曾经听过术语“B” 树或“B+ 树”，它们都是二叉搜索树的变种，数据库的索引结构就是这两种树。

二分查找和二叉搜索树不仅在数据库这种大型软件中发挥作用，实际上我们可能已经直接与它们交互过了。

举个例子，如果你曾经在项目中引入了一个错误，你可能已经使用过 Git 的 git bisect命令。根据 Git 的文档，这个命令可以帮助你在所有提交的历史记录中查找问题的源头。

使用 git bisect 时，你首先需要指定一个包含错误的“坏”提交和一个在错误出现前的“好”提交。然后，Git 会在这两个提交之间选择一个中间提交，并询问你这个提交是“好”还是“坏”。它会继续缩小范围，直到找到引入问题的具体提交。

这背后的原理是什么呢？正是通过二分查找的原理在幕后发挥作用，帮助你快速锁定问题的根源。

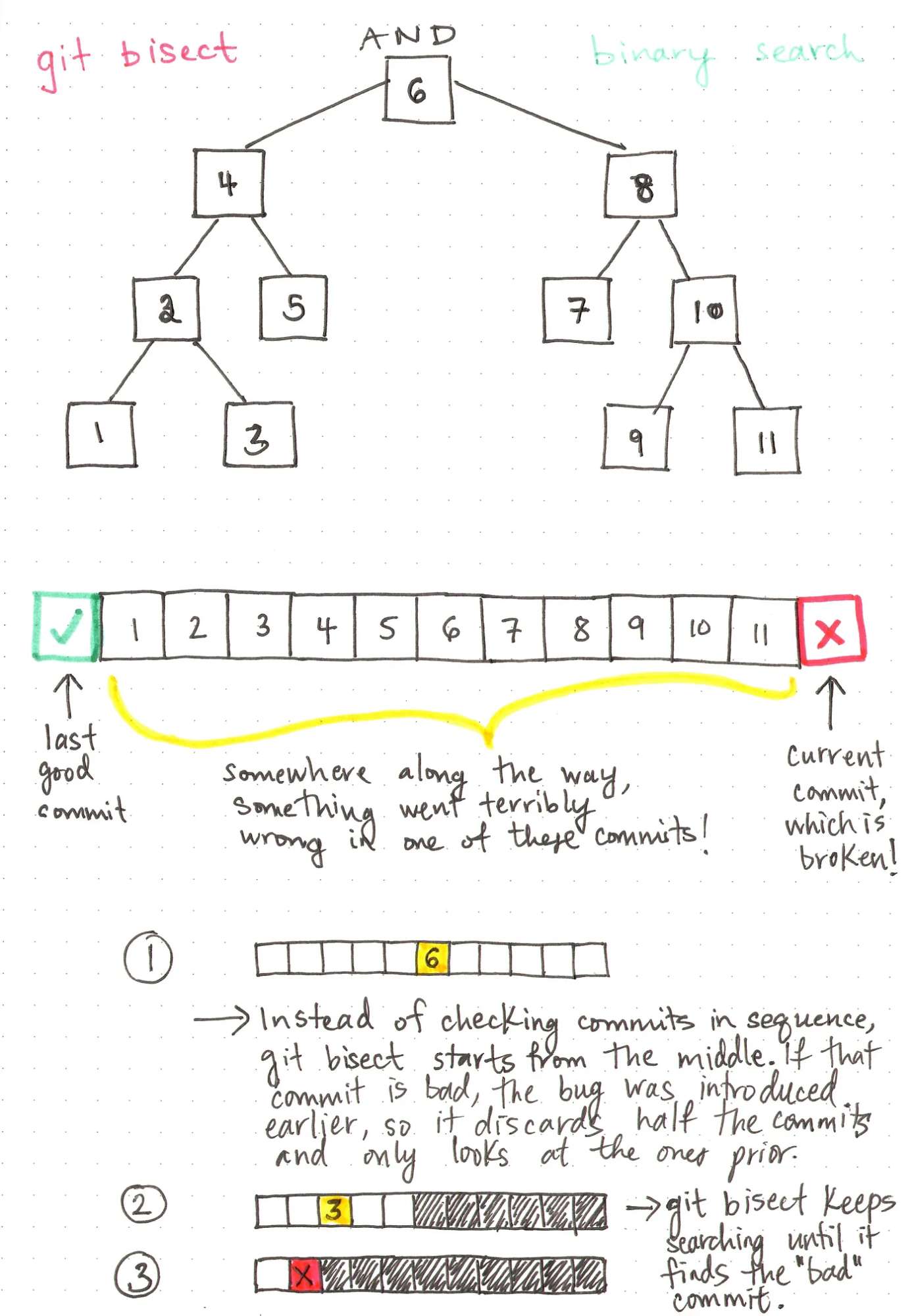
当你告诉 Git 最后一次“好的”提交是什么时候，它会搜索从那个时间点到现在的所有提交。但它并不会按时间顺序搜索，而是从中间的某个提交开始。如果你确认这个中间的提交也是“坏的”，它就会继续向前查找，并排除所有后续的提交。这正是二分查找的核心思想，正如我们今天讨论的那样！

是不是很神奇？谁能想到我们在调试高级项目时，竟然依赖如此简单的概念？！

show me the code

二叉查找树节点的定义

public class BSTree<T extends Comparable<T>> {

    private BSTNode<T> mRoot;    // 根结点

    public class BSTNode<T extends Comparable<T>> {
        T key;                // 关键字(键值)
        BSTNode<T> left;      // 左孩子
        BSTNode<T> right;     // 右孩子
        BSTNode<T> parent;    // 父结点

        public BSTNode(T key, BSTNode<T> parent, BSTNode<T> left, BSTNode<T> right) {
            this.key = key;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
    }
}

二叉树遍历

/*
前序遍历:
若二叉树非空，则执行以下操作：
(01) 访问根结点；
(02) 先序遍历左子树；
(03) 先序遍历右子树。
*/
private void preOrder(BSTNode<T> tree) {
    if(tree != null) {
        System.out.print(tree.key+" ");
        preOrder(tree.left);
        preOrder(tree.right);
    }
}

public void preOrder() {
    preOrder(mRoot);
}

/*
中序遍历:
若二叉树非空，则执行以下操作：
(01) 中序遍历左子树；
(02) 访问根结点；
(03) 中序遍历右子树。
*/
private void inOrder(BSTNode<T> tree) {
    if(tree != null) {
        inOrder(tree.left);
        System.out.print(tree.key+" ");
        inOrder(tree.right);
    }
}

public void inOrder() {
    inOrder(mRoot);
}

/*
后序遍历:
若二叉树非空，则执行以下操作：
(01) 后序遍历左子树；
(02) 后序遍历右子树；
(03) 访问根结点。
*/
private void postOrder(BSTNode<T> tree) {
    if(tree != null)
    {
        postOrder(tree.left);
        postOrder(tree.right);
        System.out.print(tree.key+" ");
    }
}

public void postOrder() {
    postOrder(mRoot);
}

查找

/*
 * (递归实现)查找"二叉树x"中键值为key的节点
 */
private BSTNode<T> search(BSTNode<T> x, T key) {
    if (x==null)
        return x;

    int cmp = key.compareTo(x.key);
    if (cmp < 0)
        return search(x.left, key);
    else if (cmp > 0)
        return search(x.right, key);
    else
        return x;
}

public BSTNode<T> search(T key) {
    return search(mRoot, key);
}


/*
 * (非递归实现)查找"二叉树x"中键值为key的节点
 */
private BSTNode<T> iterativeSearch(BSTNode<T> x, T key) {
    while (x!=null) {
        int cmp = key.compareTo(x.key);

        if (cmp < 0) 
            x = x.left;
        else if (cmp > 0) 
            x = x.right;
        else
            return x;
    }

    return x;
}

public BSTNode<T> iterativeSearch(T key) {
    return iterativeSearch(mRoot, key);
}

最大值和最小值

/* 
 * 查找最大结点：返回tree为根结点的二叉树的最大结点。
 */
private BSTNode<T> maximum(BSTNode<T> tree) {
    if (tree == null)
        return null;

    while(tree.right != null)
        tree = tree.right;
    return tree;
}

public T maximum() {
    BSTNode<T> p = maximum(mRoot);
    if (p != null)
        return p.key;

    return null;
}

/* 
 * 查找最小结点：返回tree为根结点的二叉树的最小结点。
 */
private BSTNode<T> minimum(BSTNode<T> tree) {
    if (tree == null)
        return null;

    while(tree.left != null)
        tree = tree.left;
    return tree;
}

public T minimum() {
    BSTNode<T> p = minimum(mRoot);
    if (p != null)
        return p.key;

    return null;
}

前驱和后继

节点的前驱：是该节点的左子树中的最大节点。

节点的后继：是该节点的右子树中的最小节点。

/* 
 * 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
 */
public BSTNode<T> predecessor(BSTNode<T> x) {
    // 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
    if (x.left != null)
        return maximum(x.left);

    // 如果x没有左孩子。则x有以下两种可能：
    // (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
    // (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
    BSTNode<T> y = x.parent;
    while ((y!=null) && (x==y.left)) {
        x = y;
        y = y.parent;
    }

    return y;
}


/* 
 * 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
 */
public BSTNode<T> successor(BSTNode<T> x) {
    // 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
    if (x.right != null)
        return minimum(x.right);

    // 如果x没有右孩子。则x有以下两种可能：
    // (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
    // (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
    BSTNode<T> y = x.parent;
    while ((y!=null) && (x==y.right)) {
        x = y;
        y = y.parent;
    }

    return y;
}

插入节点

/* 
 * 将结点插入到二叉树中
 *
 * 参数说明：
 *     tree 二叉树的
 *     z 插入的结点
 */
private void insert(BSTree<T> bst, BSTNode<T> z) {
    int cmp;
    BSTNode<T> y = null;
    BSTNode<T> x = bst.mRoot;

    // 查找z的插入位置
    while (x != null) {
        y = x;
        cmp = z.key.compareTo(x.key);
        if (cmp < 0)
            x = x.left;
        else
            x = x.right;
    }

    z.parent = y;
    if (y==null)
        bst.mRoot = z;
    else {
        cmp = z.key.compareTo(y.key);
        if (cmp < 0)
            y.left = z;
        else
            y.right = z;
    }
}

/* 
 * 新建结点(key)，并将其插入到二叉树中
 *
 * 参数说明：
 *     tree 二叉树的根结点
 *     key 插入结点的键值
 */
public void insert(T key) {
    BSTNode<T> z=new BSTNode<T>(key,null,null,null);

    // 如果新建结点失败，则返回。
    if (z != null)
        insert(this, z);
}

删除节点

/* 
 * 删除结点(z)，并返回被删除的结点
 *
 * 参数说明：
 *     bst 二叉树
 *     z 删除的结点
 */
private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z) {
    BSTNode<T> x=null;
    BSTNode<T> y=null;

    if ((z.left == null) || (z.right == null) )
        y = z;
    else
        y = successor(z);

    if (y.left != null)
        x = y.left;
    else
        x = y.right;

    if (x != null)
        x.parent = y.parent;

    if (y.parent == null)
        bst.mRoot = x;
    else if (y == y.parent.left)
        y.parent.left = x;
    else
        y.parent.right = x;

    if (y != z) 
        z.key = y.key;

    return y;
}

/* 
 * 删除结点(z)，并返回被删除的结点
 *
 * 参数说明：
 *     tree 二叉树的根结点
 *     z 删除的结点
 */
public void remove(T key) {
    BSTNode<T> z, node; 

    if ((z = search(mRoot, key)) != null)
        if ( (node = remove(this, z)) != null)
            node = null;
}