【数据结构】搜索树、词典、优先级队列、字符串、排序算法

数据结构

本文参考邓俊辉老师的教材《数据结构（C++语言版）》及mooc课程，总结7-12章

邓老师上课的所有资源均已公开：https://dsa.cs.tsinghua.edu.cn/~deng/ds/dsacpp/index.htm

第七章 搜索树

查找

• 不同词条之间，依照各自的关键码（key）彼此区分，查找过程与数据对象的物理位置或逻辑次序均无关，称作循关键码访问（call-by-key）；
• 数据对象，表示为词条（entry），拥有成员变量key和value；

二叉搜索树（BST）

• 顺序性：任一节点r 的左（右）子树中 ，所有节点（ 若存在）均不大于（不小于）r；

  

• 中序遍历序列：任何一棵二叉树是二叉搜索树，当且仅当其中序遍历序列单调非降；

• BST模板类（派生自BinTree）

  

• 查找算法：减而治之，逐步深入（与有序向量的二分查找过程等效）；

  

  • 接口实现（递归）

    

    

  • 若查找失败，将此空节点转换为一个数值为e的哨兵节点；

  • 效率：所需时间线性正比于查找路径的长度（最好O(1），最差O(n)）；

• 插入算法

  

  

  • 时间复杂度取决于新节点的深度；

• 删除算法

  

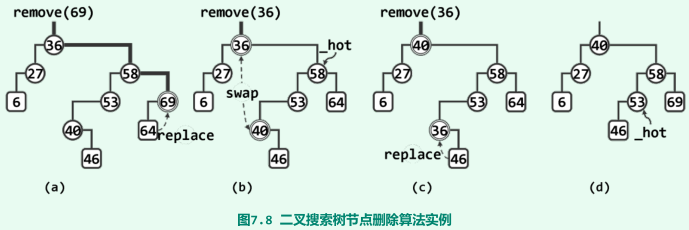
  • 删除节点为单分支则与其孩子交换、双分支则先与其后继交换；

    

    

  • 效率：不超过全树的高度。

平衡二叉搜索树（BBST）

• 二叉搜索树的性能主要取决于高度，故在节点数目固定的前提下，应尽可能地降低高度；

  • 理想平衡：树高恰好为log2n，称作理想平衡树；
  • 适度平衡：将树高限制为“渐进地不超过O(logn)”，如AVL树，伸展树、红黑树、kd-树等；

• 等价二叉搜索树：中序遍历序列相同（连接关系不尽相同，但上下可变，左右不乱）；

• 旋转调整（等价变换）

  • zig

    

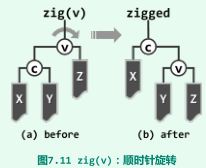
  • zag

    

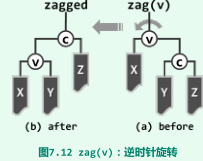
AVL树

• 属于BBST，在渐进意义下，AVL树可始终将其高度控制在O(logn)以内，从而保证每次查找、插入或删除操作，均可在**O(logn)**的时间内完成；

• 定义：

  • 平衡因子：左、右子树的高度差；
  • 对AVL树，其中各节点平衡因子的绝对值均不超过1；
  • 失衡与重平衡：因节点x的插入或删除而暂时失衡的节点，构成失衡节点集UT(x)，若x为被摘除的节点，则UT(x)仅含单个节点；但若x为被引入的节点，则UT(x)可能包含多个节点；

• 节点插入及重平衡

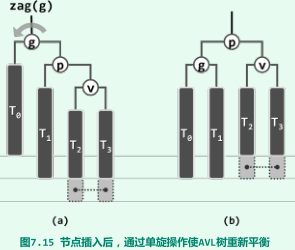
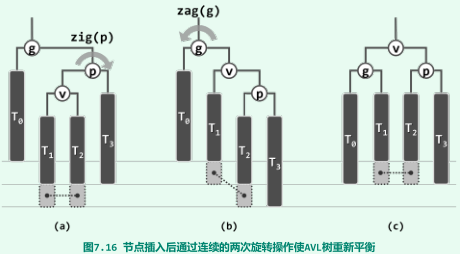
  • 失衡节点集：最深为g(x)，p(x)为g(x)的孩子，v为p(x)的孩子；

  • 重平衡：

    • p，g，v同向：单旋（zig或zag）

      

    • p，g，v不同向：双旋（zigzag或zagzig）

      

  • 局部调整之后，g(x)能够重获平衡，而且局部子树的高度也必将复原，即在AVL树中插入新节点后，仅需不超过两次旋转，即可使整树恢复平衡。

  • 效率：O(logn)；

• 节点删除及重平衡

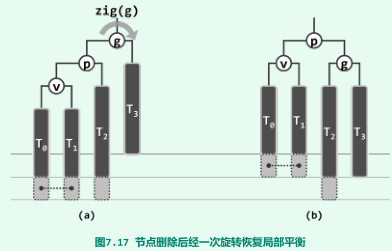
  • 失衡节点集UT(x)始终至多只含一个节点，g，p，v与上文同理；

  • 重平衡

    • 单旋

      

    • 双旋

      

    • 失衡传播：

      • 在删除节点之后，尽管也可通过单旋或双旋调整使局部子树恢复平衡，但就全局而言，依然可能再次失衡（因为重平衡后局部子树的高度可能再次降低）；
      • 失衡传播的方向必然自底而上，可逐层遍历失衡祖先并进行处理；

  • 效率：O(logn)。

• 统一重平衡算法（3 + 4重构）

  • 找到最低的失衡节点g(x)，以g(x)、p和v为界，分解为四棵子树（T0-T3）；

  • 按照中序遍历次序，重新排列g(x)、p和v，并将其命名为a、b和c，则这一局部的中序遍历序列应为：{ T0 , a, T1 , b, T2 , c, T3 }

    

    

  • 利用以上connect34()算法，即可视不同情况，按如下具体方法完成重平衡

    

高级搜索树

伸展树

• 属于BBST，无需时刻都严格地保持全树的平衡，不需要记录平衡因子或高度之类的额外信息；

• 数据局部性

  

  • 因此需要将刚访问过的节点转移至树根附近。

• 逐层伸展（单次访问的分摊时间复杂度可能高达Ω(n)）

  

• 双层伸展（单次访问的分摊时间复杂度均在O(logn)）

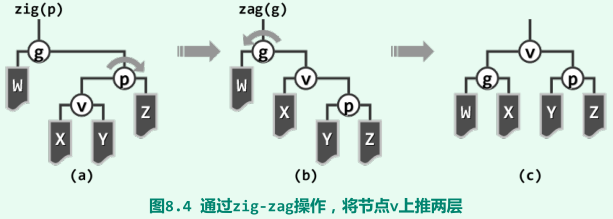
  • zig-zig/zag-zag

    

  • zig-zag/zag-zig

    

  • zig/zag

    

• 伸展树（Splay）的实现

  

  • 查找算法：

    • 可调用二叉搜索树的标准插入算法BST::insert()；

    • Splay::search() + Splay::insert()：搜索–伸展 + 分裂–插入

      

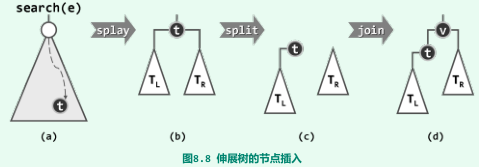
  • 删除算法

    • 可调用二叉搜索树标准的节点删除算法BST::remove()；

    • Splay::search() + Splay::remove()：搜索–伸展 + 释放–伸展–合并

      

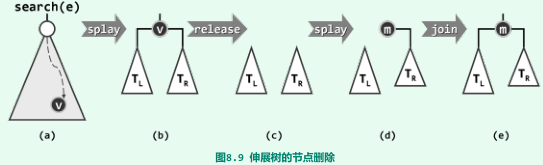
B树

• 多路平衡查找

  • 分级存储：将内存作为外存的高速缓存，存放最常用数据项的
    复本，将内存的“高速度”与外存的“大容量”结合起来，可以忽略对内存的访问，转而更多地关注对外存的访问次数；

  • 多路搜索树：将通常的二叉搜索树，改造为多路搜索树（在中序遍历的意义下，这也是一种等价变换）；

    

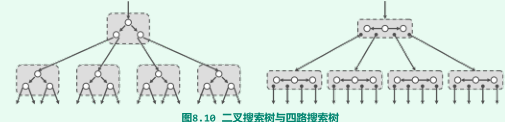
  • 原理：

    • 可以两层为间隔，将各节点与其左、右孩子合并为“大节点”；
    • 搜索每下降一层，都以“大节点”为单位从外存读取一组（而不再是单个）关键码。这组关键码在逻辑上与物理上都彼此相邻，故可以批量方式从外存一次性读出，且所需时间与读取单个关键码几乎一样。

• 多路平衡搜索树

  • m路平衡搜索树，即m阶B-树（B-tree）

    

    • 分支：[m/2取上整，m]，故m阶B-树也称作(m/2取上整, m)-树；
    • 内部节点内关键码数：[(m/2取上整)-1, m-1]；
    • 外部节点：叶节点的数值为空的孩子，所有外部节点深度均相等；

  • 表示

    

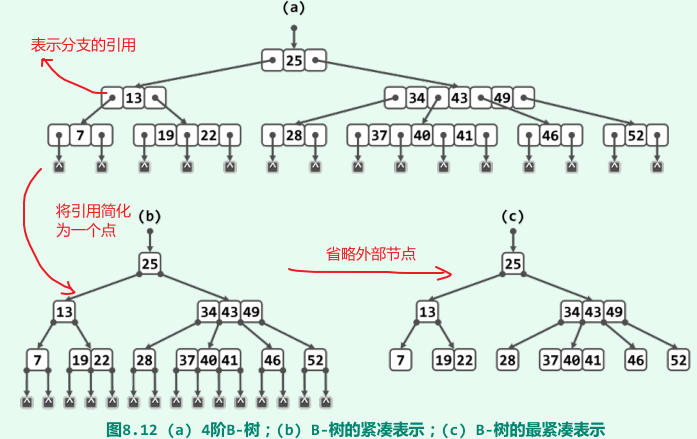
• ADT接口及其实现

  • 节点

    

  • B-树模板类

    

• 关键码查找

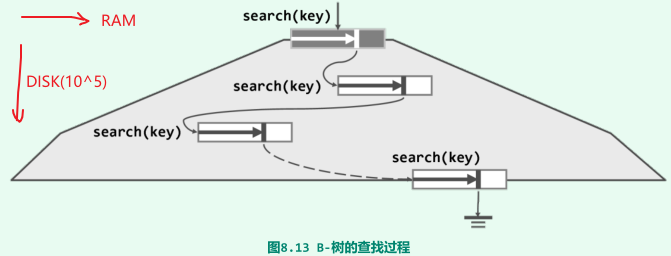
  • 原理：将大数据集组织为B-树并存放于外存，根节点会常驻于内存，任何时刻通常只有另一节点（称作当前节点）留驻于内存；

    

  • 实现

    

  • 性能

    • B-树的每一次查找过程中，在每一高度上至多访问一个节点即对于高度为h的B-树，外存访问不超过O(h - 1)；

    • 树高h（m为最大分支树，N为关键码数）

      

      最大树高：O(log_m_N)；

      最小树高：Θ(log_m_N)；

      渐进意义：Ω(log_m_N)；

    • 复杂度：O(log_m_N)，没有渐进意义上的改进，但极其耗时的I/O操作的次数，已大致缩减为原先的1/log_2_m；

• 关键码插入

  

  • 上溢与分裂

    • 原因：_hot所指的节点中增加了一个关键码后，总数超过m-1个；
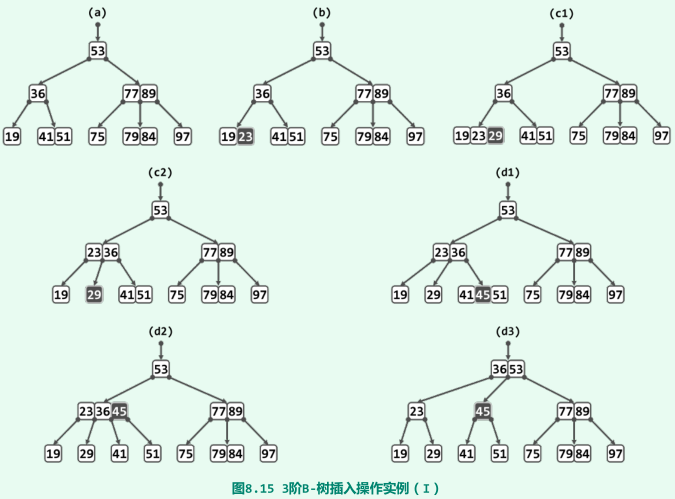
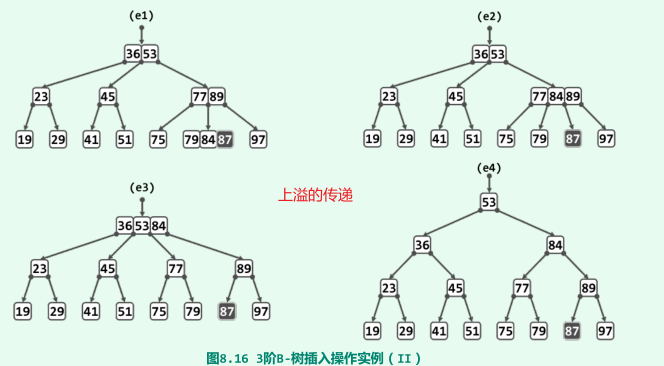
    • 分裂：取发生上溢的节点的居中节点，将该节点分前、后两个子节点，再另居中节点上升一层，归入其父节点中的适当位置，并以两个子节点作为其左右孩子；

    

    • 实例（3阶B-树，关键码数目不超过2）

      

      

    • 上溢的传递（最多到根节点）；

    • 复杂度：O(log_m_N)；

• 关键码删除

  

  • 下溢与合并

    • 原因：关键码总数少于(m/2取上整)-1；

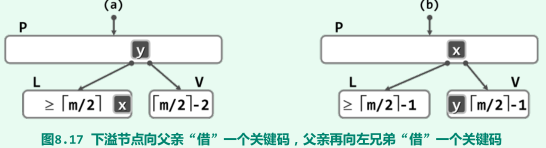
    • 合并：左顾右盼，并进行旋转

      1. V的左兄弟L存在，且至少包含m/2取上整个关键码

         

      2. V的右兄弟R存在，且至少包含m/2取上整个关键码

         

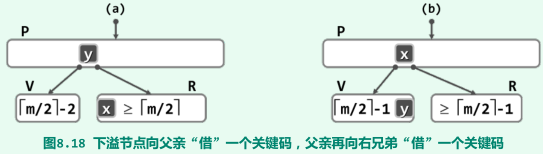
      3. V 的左、右兄弟L和R 或者不存在，或者其包含的关键码均不足m/2取上整个

         

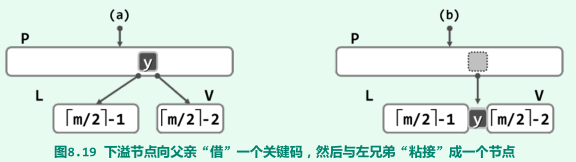
    • 实例（3阶B-树，关键码数目不少于1）

      

      

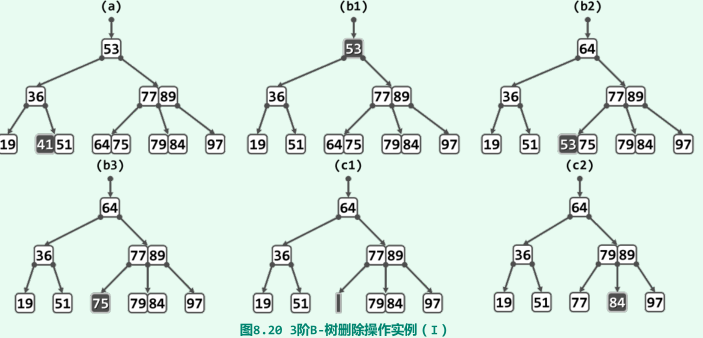
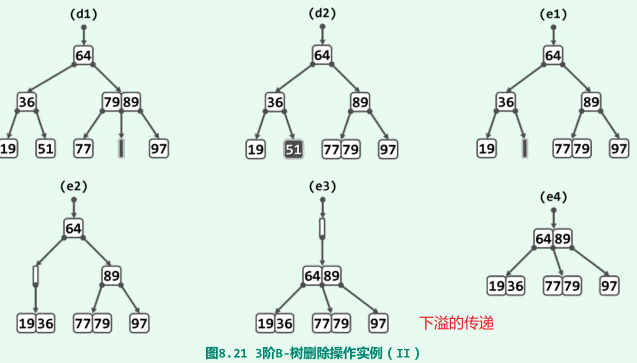
    • 下溢的传递，最多到根节点（全树高度也随之下降一层）；

    • 复杂度：O(log_m_N)；

红黑树

• 概述

  • AVL树：插入后可能需要O(1)旋转后复原，删除后可能需要O(logn)旋转后才能复原，导致全树整体拓扑结构的大幅度变化；
  • 红黑树：每次插入或删除操作之后的重平衡过程中，全树拓扑结构的更新仅涉及常数个节点，最坏情况下需对Ω(logn)个节点重染色，但就分摊意义而言仅为O(1)个；
  • 适度平衡：任一节点左、右子树的高度，相差不得超过两倍；

• 定义与性质

  • 由红、黑两色节点组成的二叉搜索树若满足以下条件，即为红黑树

    

    • 从根节点通往任一节点的沿途，黑节点都不少于红节点；
    • 黑深度：从根节点通往任一节点的沿途，除去根节点本身，沿途所经黑节点的总数；
    • 黑高度：从任一节点通往其任一后代外部节点的沿途，除去（黑色）外部节点，沿途所经黑节点的总数称作该节点的黑高度，黑节点的总数亦必相等；

  • (2,4)-树

    • 经适当转换之后，红黑树与(2,4)-树相互等价；

    • 转换方式：每遇到一个红节点，都将对应的子树整体提升一层，从而与其父节点（必黑）水平对齐，二者之间的联边则相应地调整为横向；

    • 将原红黑树的节点视作关键码，沿水平方向相邻的每一组（父子至多三个）节点即恰好构成4阶B-树的一个节点；

    • 四种情况的转化

      

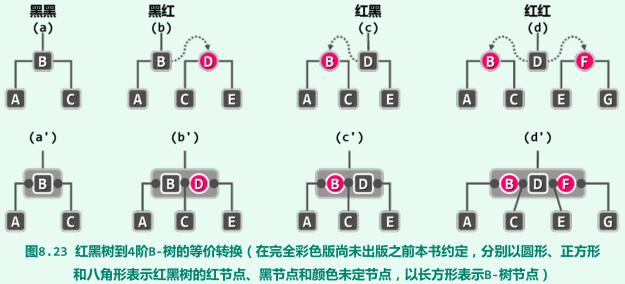
      (2,4)-树中的每个节点应包含且仅包含一个黑关键码，同时红关键码不得超过两个。

  • 平衡性

    • 包含n个内部节点的红黑树T的高度h不超过O(logn)，保证了适度平衡；
    

• 红黑树接口定义

  

• 节点插入算法

  • 创建节点x，染成红色（为满足红黑树条件1、2、4）；

  • 若因新节点的引入导致父子同为红色，进行双红修正：

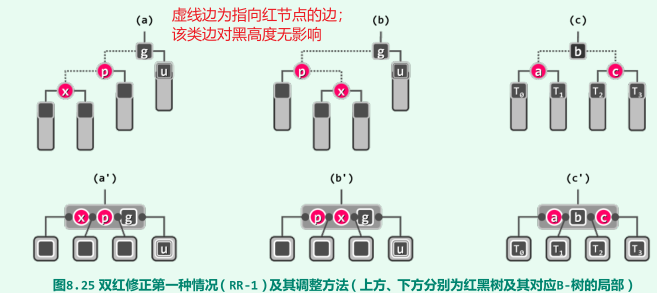
    • RR-1：x的叔父u为黑，此时，x的兄弟、两个孩子的黑高度与u相等：此时令黑色关键码与紧邻的红色关键码互换颜色，等效于按中序遍历次序，对节点x、p和g及其四棵子树，做一次局部“3 + 4”重构，局部子树的黑高度将复原；

      

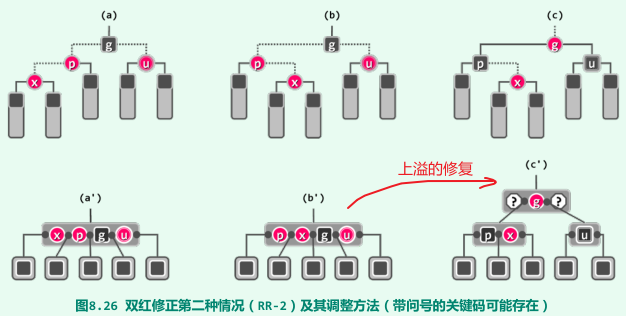
    • RR-2：x的叔父u为红，此时需将红节点p和u转为黑色，黑节点g转为红色，x保持红色，等效于B树上溢的修复，但可能导致上溢的传播（将g视为新节点，继续按双红进行修复）；

      

  • 双红修正复杂度：至多做O(logn)次节点染色（均只需常数时间），1次“3 + 4”重构（一但旋转，修复过程必然完成），就全树拓扑结构而言，每次插入后仅涉及常数次调整。

• 节点删除算法（将红黑树转化为B树进行理解）不太懂

  • 删除节点x，p = _hot为其父亲，r为其接替者（红黑树条件3、4可能不满足）

  • 若x与r一黑一红，则可通过重染色的方式恢复局部子树黑高度；

  • 若x与r均为黑色，则需进行双黑修正，其中原黑节点x的兄弟必然非空，将其记作s；

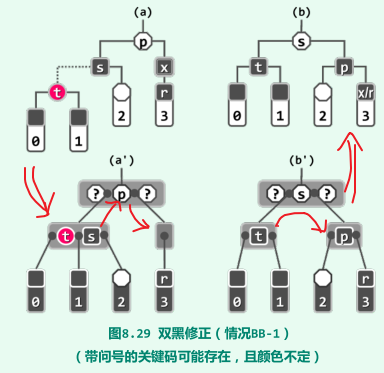
    • BB-1：s为黑，且至少有一个红孩子（对应于B树，即为兄弟节点足够富裕），此时将t和p染成黑色，s继承p此前的颜色，等效于对节点t、s和p实施“3 + 4”重构；

      

    • BB-2-R：s为黑，且两个孩子均为黑，p为红（对应于B树中，下溢节点与兄弟合并），此时将s和p颜色互换；

      

    • BB-2-B：s为黑，且两个孩子为黑，p为黑，此时将节点s由黑转红

      

    • BB-3：s为红，其孩子均为黑，此时将s与p互换颜色，对应于以节点p为轴做一次旋转

      

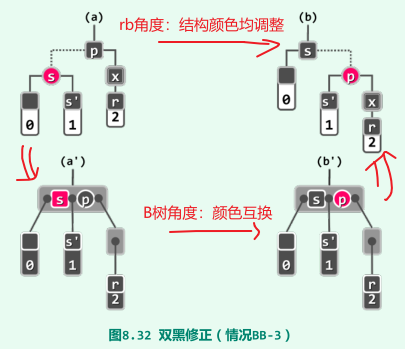
  • 双黑修正复杂度：至多做O(logn)次节点染色（均只需常数时间），1次“3 + 4”重构（一但旋转，修复过程必然完成），1次单旋，就全树拓扑结构而言，每次删除后仅涉及常数次调整。

第9章 词典

• 词典（dictionary）结构，是由一组数据构成的集合，其中各元素都是由关键码和数据项合成的词条（entry）；
• 以散列表为代表的符号表结构，将依据数据项的数值直接做逻辑查找和物理定位，关键码（key）与数值（value）的地位等同，即循值访问（call-by-value）。

词典ADT

跳转表

• 跳转表是一种高效的词典结构，定义与实现基于有序列表，其查询和维护操作在平均的意义下均仅需**O(logn)**时间；

• Skiplist模板类

  

• 总体逻辑结构

  • 内部由沿横向分层、沿纵向相互耦合的多个列表{ S_0 ,S_1 , S_2 , …, S_h }组成，h称作跳转表的高度；

    

• 四联表：跳转表内各节点沿水平和垂直方向都可定义前驱和后继，支持这种联接方式的表称作四联表（quadlist），它是Skiplist模板类的底层实现方式。

• 查找、插入、删除复杂度均为O(logn)，具体实现参考P252-P259。

散列表

• 完美散列

  • 散列表（hashtable）：散列方法的底层基础，逻辑上由一系列可存放词条的单元组成，称作桶（bucket）或桶单元，各桶单元也应按其逻辑次序在物理上连续排列，这种线性的底层结构用向量来实现；
  • 散列函数（hash function）：从关键码空间到桶数组地址空间的函数（然后再找到词条），即hash() : key -> hash(key)；

• 装填因子：非空桶的数目与桶单元总数的比值；

• 散列函数：

  • 关键码均为[0, R)范围内的整数、词条数记作N、散列表长度记作M，则有：R >> M > N；

  • 散列函数hash()的作用可理解为，将关键码空间[0, R)压缩为散列地址空间[0, M)；

    

  • 设计原则：确定性（同一关键码映射到同一散列地址）快速、最好满射、最好均匀；

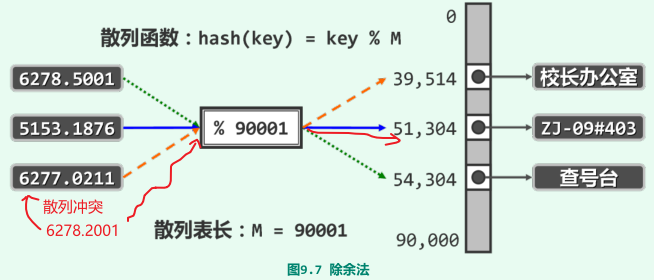
  • 散列冲突（collision）：关键码不同的词条被映射到同一散列地址；

• 常见散列函数

  • 除余法：将散列表长度M取作为素数（降低聚集发生的概率），并将关键码key映射至key关于M整除的余数，即hash(key) = key mod M

    

  • MAD法（multiply-add-divide method）：消除关键码空间到散列地址空间映射的连续性，将关键码key映射为(a × key + b ) mod M，其中M仍为素数，a > 0，b > 0，且a mod M ≠ 0；

    

  • 数字分析法：从关键码key特定进制的展开中抽取出特定的若干位，构成一个整型地址；

  • 折叠法：将关键码的十进制或二进制展开分割成等宽的若干段，取其总和作为散列地址；

  • 位异或法：将关键码的二进制展开分割成等宽的若干段，经异或运算得到散列地址；

  • （伪）随机数法。

• 散列表

  • Hashtable 模板类

    

• 冲突及其排解

  • 多槽位法：绝大多数的槽位通常都处于空闲状态，装填因子降低至原先的1/k，且冲突可能于某个特定桶单元，导致溢出；

    

  • 独立链法：需申请额外空间，且查找过程中一旦发生冲突，则需要遍历整个列表，导致查找成本的增加；

    

  • 公共溢出区法

    

• 闭散列策略（开放定址）：散列地址空间对所有词条开放，每个桶单元都有可能存放任一词条；

  • 线性试探法

    

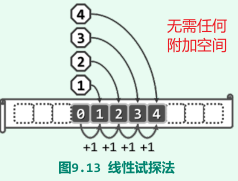
    • 第i次试探的桶单元应为：ht[ (hash(key) + i) mod M ]， i = 1, 2, 3, …

  • 查找链：采用开放地址策略时，散列表中每一组相互冲突的词条都将被视作一个有序序列，对其中任何一员的查找都需借助这一序列，查找链平均长度为n/2取上整；

  • 懒惰删除：

    • 查找链中任何一环的缺失，都会导致后续词条因无法抵达而丢失，若采用开放定址策略，则在执行删除操作时，需同时做特别的调整；
    • 为每个桶另设一个标志位，指示该桶尽管目前为空，但此前确曾存放过词条，如此，该桶虽不存放任何实质的词条，却依然是查找链上的一环；

  • 两类查找

    • probe4Hit()：在删除等操作之前对某一目标词条的查找，对成功的判定条件基本不变，对失败的判定条件需兼顾懒惰删除标志（即带有懒惰删除标志时将沿着查找链继续试探）；
    • probe4Free()：在插入等操作之前沿查找链寻找空桶，无论当前桶为空，还是带有懒惰删除标记，均可报告“查找成功”；

• 查找与删除

  • probe4Hit(k) + remove()；

• 插入

  

  • 装填因子：建议保持λ< 0.5；

  • 重散列（rehashing ）

    

• 更多闭散列策略

  • 聚集现象：线性试探法各查找链均由物理地址连续的桶单元组成，会加剧关键码的聚集趋势；

  • 平方试探法

    

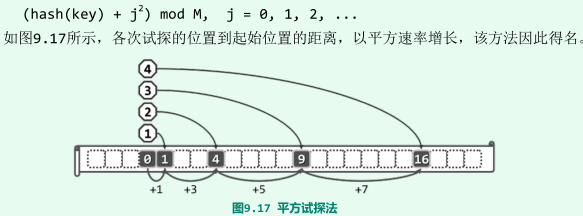
    • 试探位置的间距将以线性（而不再是常数1的）速度增长，一旦发生冲突，即可“聪明地”尽快“跳离”关键码聚集的区段；
    • 只要散列表长度M为素数且装填因子λ ≤ 50%，则平方试探迟早必将终止于某个空桶；

  • （伪）随机试探法；

  • 再散列法：选取二级散列函数hash_2()，发生冲突时以hash_2()为偏移增量继续尝试，直到发现一个空桶；

    

• 散列码转换

  • 关键码不仅限定为整数，首先利用散列码转换函数hashCode()将关键码key转换为一个整数（称作散列码（hash code））；然后再利用散列函数将散列码映射为散列地址；

    

  • byte、short、int和char等强制转换为整数，作为散列码；

  • long long和double之类长度超过32位的基本类型，将高32位和低32位分别看作两个32位整数，将二者之和作为散列码；

  • 多项式散列码：将字符串中的各个字符对应到整数，将多项式的和作为散列码：

    

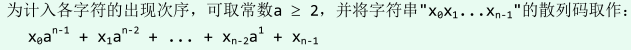
第10章 优先级队列

• 优先级队列：按照事先约定的优先级，可以始终高效查找并访问优先级最高数据项的数据结构；
• 仿照词典结构，将优先级队列中的数据项称作词条（entry），与特定优先级相对应的数据属性，也称作关键码（key）；
• 关键码之间必须可以比较大小。

优先级队列ADT

• 操作接口

  

• 接口定义

  

堆

• 优先级队列的实现方法

  • 效率过高：BBST；
  • 效率低：list（O(1)但getmax()需要O(n)）、vector（查找及顺次后移需要O(n)）；
  • 效率合理：堆(heap)：仅维持偏序关系（即足以确定极值元素）、形（vector）+神（tree）；

• 完全二叉堆

  • 结构性：逻辑结构须等同于完全二叉树；

  • 堆序性：堆顶以外的每个节点优先级都不高（大）于其父节点；

  • 大顶堆与小顶堆；

  • 高度：n个词条组成的堆的高度h = log2n = O(logn)，insert()和delMax()的时间复杂度线性正比于堆的高度h，故它们均可在O(logn)的时间内完成；

  • 基于向量的紧凑表示：按照层次遍历的次序，若将所有节点组织为一个向量，则堆中各节点（编号）与向量各单元（秩）将彼此一一对应；

    

  • 

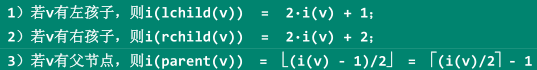
• 完全二叉堆的实现

  

  

• 元素插入O(logn)

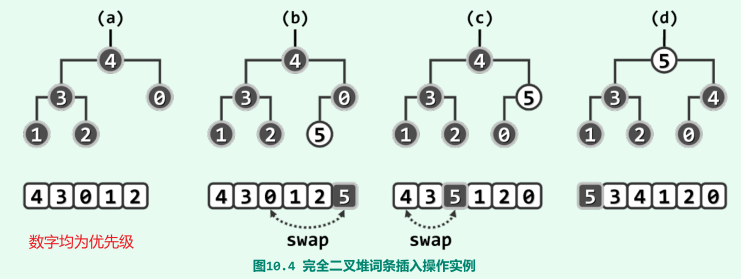
  • 步骤：将新词条接至向量末尾，再对该词条实施上滤调整；

  • 上滤：当前节点优先级大与其父节点，交换这两个节点；

    • 最坏情况：上滤至堆顶（O(nlogn)）；
    • 平均上升为O(1)，即总平均时间复杂度为O(logn)；

  • 实例

    

  • 实现

    

• 元素删除O(logn)

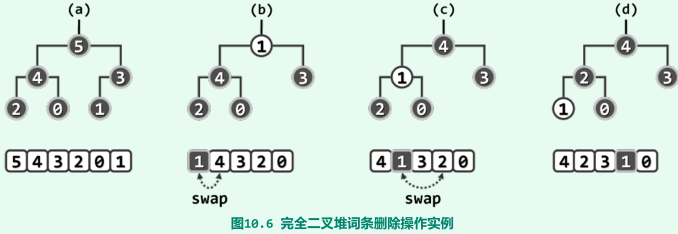
  • 步骤：摘除堆顶（首词条），代之以末词条，随后对新堆顶实施下滤调整；

  • 下滤：若当前节点优先级小于孩子节点，则交换该节点与其孩子节点中的大者；

  • 实例

    

  • 实现

    

• 建堆

  • 蛮力算法O(nlogn)：逐条插入；

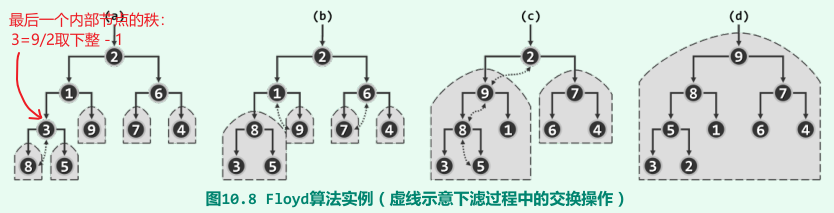
  • 自上而下的上滤O(nlogn)：将所有输入词条纳入长为n的向量之后，首单元处的词条本身可视作一个规模为1的堆，将下一单元中的词条插入当前堆并上滤，依次迭代；

  • 自下而上的下滤----Floyd算法O(n)：将所有词条组成一棵完全二叉树，然后找到最后一个内部节点，自底而上地逐层合并；

    

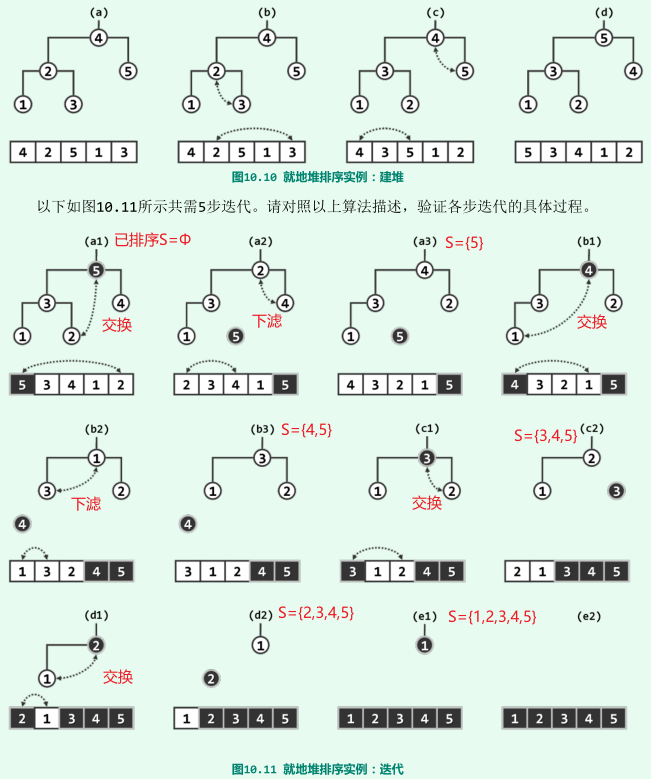
• 就地堆排序

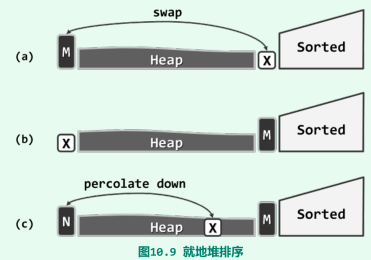
  • 原理：将所有词条分成未排序（组织为一个堆）和已排序两类，不断从前一类中取出最大者（堆顶M），顺序加至后一类中；

  • 当与M交换的x无法胜任堆顶时，实施下滤；

    

  • 复杂度：O(nlogn)，实际运行效率往往要高于其它O(nlogn)的算法；

  • 实例

    

  • 实现

    

左式堆

• 堆合并：对于堆来说，为控制合并操作所涉及的节点数，反而需要保持某种意义上的“不平衡”；

• 单侧倾斜：

  • 左式堆（leftist heap）是优先级队列的另一实现方式，可高效地支持堆合并操作，具体地，需参与调整的节点不超过O(logn)个；
  • 左式堆节点分布偏向左侧，合并操作只涉及右侧；

• PQ_LeftHeap模板类

  

• 空节点路径长度（null path length），记作npl(x)，节点x的npl值取决于其左、右孩子npl值中的小者：

  • npl(x) = 1 + min( npl(lc(x)), npl(rc(x)) )

    

  • npl(x)既等于x到外部节点的最近距离（该指标由此得名），同时也等于以x为根的最大满子树（图中以矩形框出）的高度；

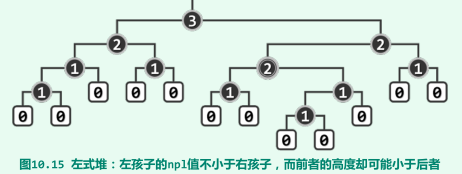
• 左倾性与左式堆

  • 左式堆是处处满足“左倾性”的二叉堆，即任一内部节点x都满足:

    npl(lc(x)) ≥ npl(rc(x))，即任一内部节点的左孩子都不小于其右孩子；

    

  • 左式堆中任一内节点x都应满足：

    npl(x) = 1 + npl(rc(x))，即左式堆中每个节点的npl值，仅取决于其右孩子；

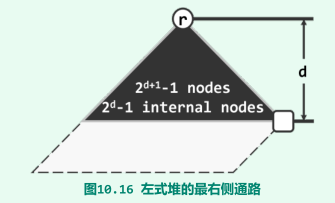
• 最右侧通路

  • 从x出发沿右侧分支一直前行直至空节点，经过的通路称作其最右侧通路，记作rPath(x)；

  • 每个节点的npl值，应恰好等于其最右侧通路的长度；

    

  • rPath®的终点必为全堆中深度最小的外部节点；

  • 最右侧通路必然不会长于O(logn)；

• 合并算法

  • 递归地将a的右子堆a_R与堆b合并，然后作为节点a的右孩子替换原先的a_R，比较a左、右孩子的npl值，如有必要还需将
    二者交换，以保证左孩子的npl值不低于右孩子；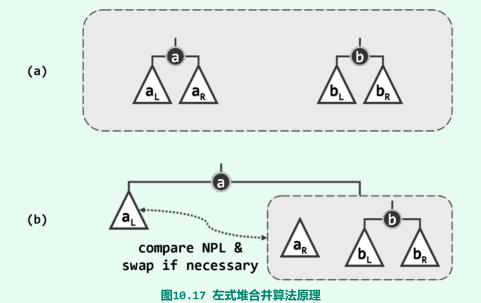

    

  • 实例

    

• 合并的实现

  

• 复杂度

  • 递归只可能发生于两个待合并堆的最右侧通路上；
  • 若待合并堆的规模分别为n和m，则其两条最右侧通路的长度
    分别不会超过O(logn)和O(logm)，合并算法总体运行时间应不超过O(log(max(n, m)))；

• 基于合并的插入和删除

  • delMax()：总体不超过O(logn)；
  • insert()：总体不超过O(logn)；

第11章 串

串及串匹配

• 串：字符串、子串、判等；

• 串匹配：如何在字符串数据中，检测和提取以字符串形式给出的某一局部特征

  

• 约定：文本串T（|T| = n ）和模式串P（|P| = m）

蛮力算法

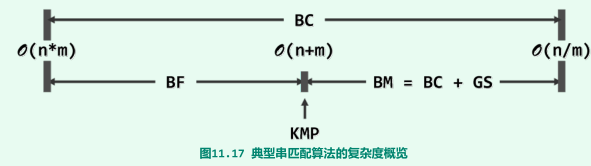
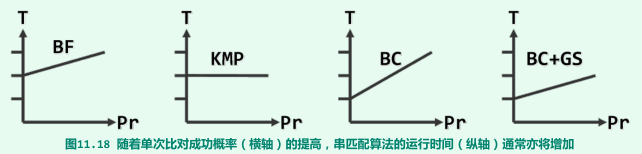
• 时间复杂度：O(n∙m)，其中，文本串长度为n、模式串长度为m；
• 在最坏情况下所需时间，为文本串长度与模式串长度的乘积，无法应用于规模稍大的应用环境；

KMP算法

• 构思

  

  • 避免文本串字符指针的回退，使模式串尽可能大跨度地右移（经验）；

• next表（P的自匹配—快速右移）

  • 假设前一轮比对终止于T[i] ≠ P[j]。按以上构想，指针i不必回退，而是将T[i]与P[t]对齐并开始下一轮比对：

    

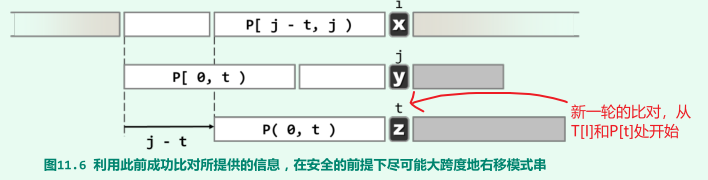
  • 若模式串P经适当右移之后，能够与T的某一（包含T[i]在内的）子串完全匹配，则：

    P[0, t) = T[i - t, i) = P[j - t, j)

    亦即，在P[0, j)中长度为t的真前缀，应与长度为t的真后缀完全匹配；

  • 具体由哪些t值构成，仅取决于模式串P以及前一轮比对的首个失配位置P[j]，与文本串T无关；

  • 为保证P与T的对齐位置（指针i）不倒退，同时又不致遗漏任何可能的匹配，应挑选最大的t，即应该保守地选择P中移动距离最短者；

  • 总结：一旦发现P[j]与T[i]失配，即可转而将P[ next[j] ]与T[i]彼此对准，并从这一位置开始继续下一轮比对；

  • 通过预处理提前计算出所有位置j所对应的next[j]值，并整理为表格----next表；

• KMP算法

  

• next[0] = -1

  • 假想地在P[0]的左侧“附加”一个P[-1]，且该字符与任何字符都是匹配的，等同于“令next[0] = -1”；

• next[j + 1]

  • 若next[j] = t，则意味着在P[0, j)中，自匹配的真前缀和真后缀的最大长度为t，故必有next[j + 1] ≤ next[j] + 1，当且仅当P[j] = P[t]时取等号；

    

  • 由next表的功能定义，next[j + 1]的下一候选者应该依次是：

    next[ next[j] ] + 1, next[ next[ next[j] ] ] + 1, …

    

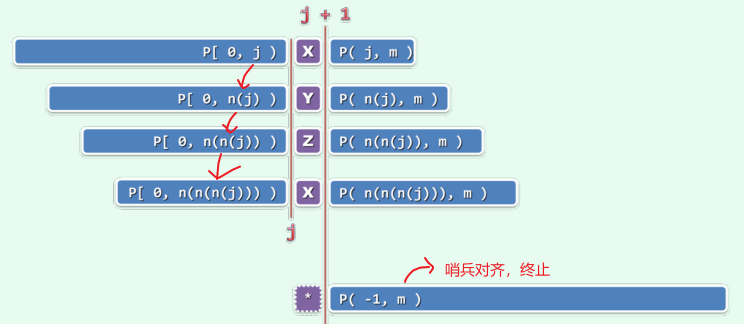
  • 因此，令t = next[t]，即可按优先次序遍历以上候选者；一旦发现P[j]与P[t]匹配（含与P[t = -1]的通配），即可令next[j + 1] = next[t] + 1；

  • 该算法必然会终止于通配的next[0] = -1；

• 构造next表

  

• KMP性能分析：总体运行时间为O(n + m)；

• 改进：

  • 除“对应于自匹配长度”以外，t只有还同时满足“当前字符对不匹配”的必要条件，方能归入集合N(P, j)并作为next表项的候选；

  

BM算法

• 模式串P与文本串T的对准位置**“自左向右”推移，在每一对准位置“自右向左”**地逐一比对各字符；

  

• 坏字符策略（bad character）

  • 失配处的字符称为坏字符，坏字符策略更多地关注教训，使之更早出现

    

  • 若P与T的某一（包括T[i + j]在内的）子串匹配，则必然在T[i + j] = X处匹配，只需找出P中的每一字符 X，分别与T[i + j] = 'X’对准，并执行一轮自右向左的扫描比对；

  • 对应于每个这样的字符X，P的位移量仅取决于原失配位置j，以及X在P中的秩，而与T和i无关；

  • bc表

    

    • 仅尝试P中最靠右的字符’X’（若存在）

  • 特殊情况

    • 若P根本就不含坏字符X，应将该串整体移过失配位置T[i + j]，用P[0]对准T[i + j + 1]，再启动下一轮比对，即将BC表中此类字符的对应项置为-1，效果也等同于在模式串的最左端，增添一个通配符；
    • 其中最靠右者的位置也可能太靠右，以至于k = bc[X] ≥ j，此时将P串右移一个字符，然后启动下一轮比对；

  • bc表构造算法

    

  • 复杂度：

    • 最好：O(n / m)；
    • 最坏：O(n × m)；

  

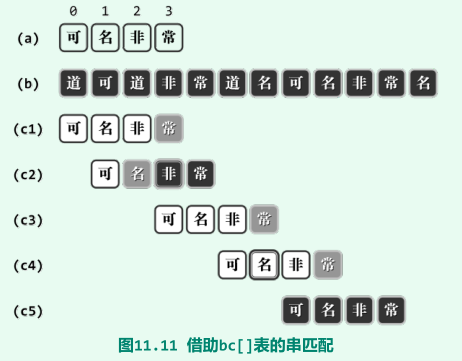
• 好后缀策略（good suffix）

  • 每轮比对中的若干次（连续的）成功匹配，都对应于模式串P的一个后缀，称作“好后缀”，好后缀策略更多地关注经验；

    

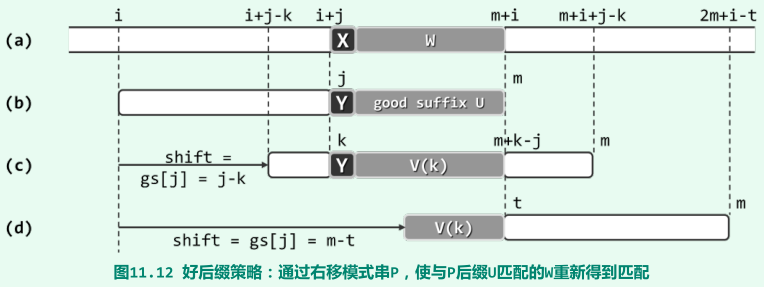
  • 若值得将P[k]与T[i + j]对齐并做新的一轮比对，则P的子串V(k)首先必须与P自己的后缀U相互匹配；

  • 另一必要条件（与KMP的改进同理）：P中这两个自匹配子串的前驱字符不得相等，即P[k] ≠ P[j]；

  • k本身（包括向右位移量j - k）仅取决于模式串P以及j值,因此可以仿照KMP算法得到gs表，取gs[j] = m - |V(k)|；

  • 且若P中没有任何子串V(k)可与好后缀U完全匹配，则应找出可与U的某一（真）后缀相匹配的最长者作为V(k)；

  

• 时间效率

  

  

第12章 排序

快速排序

• 分治策略的典型应用，将问题划分为彼此独立的两个子问题；

• 轴点

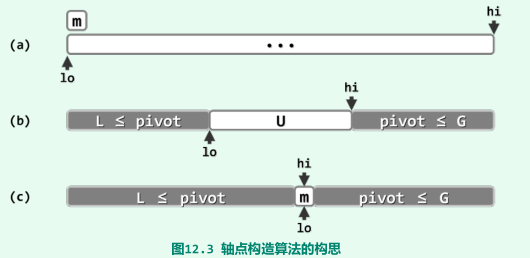
  • 队任一向量区间S[lo, hi)。对于任何lo ≤ mi < hi，若S[lo, mi)中的元素均不大于S[mi]，且S(mi, hi)中的元素均不小于S[mi]，则元素S[mi]称作向量S的一个轴点（pivot）；

    

  • 以轴点S[mi]为界，前、后子向量的排序可各自独立地进行，一旦前、后子向量各自完成排序，即可立即（在O(1)时间内）得到整个向量的排序结果；

• 快速划分算法（找轴点及划分子向量）

  • 取出首元素m = S[lo]作为候选，腾出的空闲单元便于其它元素的位置调整，不断试图移动lo和hi，使之相互靠拢；

  • 当lo与hi彼此重合时，只需将原备份的m回填至这一位置，则S[lo = hi]= m便成为一个名副其实的轴点；

    

  • 实现

    

  • 实例

    

• 复杂度：快速排序算法的平均效率可以达到O(nlogn)，且具体地，平均运行时间记作 ^ T(n) = O(1.386∙log_2_n)；

选取与中位数

• 概述

  • 中位数可将原数据集（原问题）划分为大小明确、规模相仿且彼此独立的两个子集，故能否高效地确定中位数，将直接关系到采用分治策略的算法能否高效地实现；
  • 蛮力算法，复杂度O(nlog^2_n)；

• 众数

  • 若众数存在，则必然同时也是中位数

  • 减而治之（运行时间线性正比于向量规模）

    

    • 迭代剪除前缀P可以逐步缩小问题规模；

    

• 归并向量的中位数

  

  • 减而治之（总体时间复杂度为O(logn)）

    

    • 迭代剪除S的两翼可以逐步缩小问题规模；

  

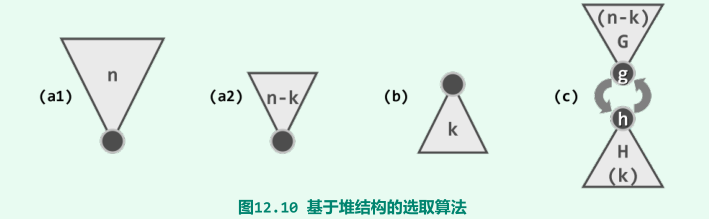
• 基于优先级队列的k选取

  

  • (a1)：将全体元素组织为一个小顶堆；然后经过k次delMin()操作，则如图(a2)所示得到位序为k的元素；

  • (b)：任取k个元素组织为大顶堆，然后将剩余的n - k个元素逐个插入堆中；每插入一个，随即删除堆顶，待所有元素处理完毕之后，堆顶即为目标元素；

  • ©：分别构建一个规模为n - k的小顶堆G和一个规模为k的大顶堆H，反复比较它们的堆顶g和h，只要g < h，则将二者交换；

  • 在目标元素的秩很小或很大时，上述算法性能较好，当k ≈ n/2时，以上算法的复杂度均退化至蛮力算法的O(nlogn)；

• 基于快速划分的k选取

  • 选取问题所查找元素的位序k，就是其在对应的有序序列中的秩；

  • 步骤：构造向量的一个轴点A[i] = x，若i = k，则该轴点恰好就是待选取的目标元素，即可直接将其返回，反之，若k < i，将子向量G剪除，然后递归地在剩余区间继续做k-选取，k＞i同理；

    

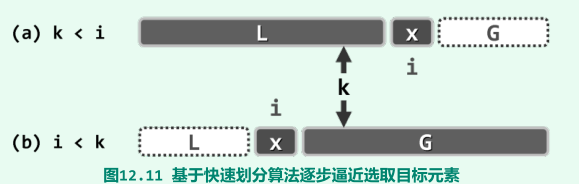
  • 最坏情况下总体运行时间为O(n^2)；

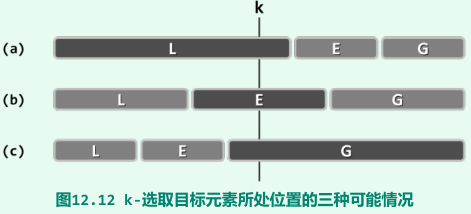
• k- 选取算法

  

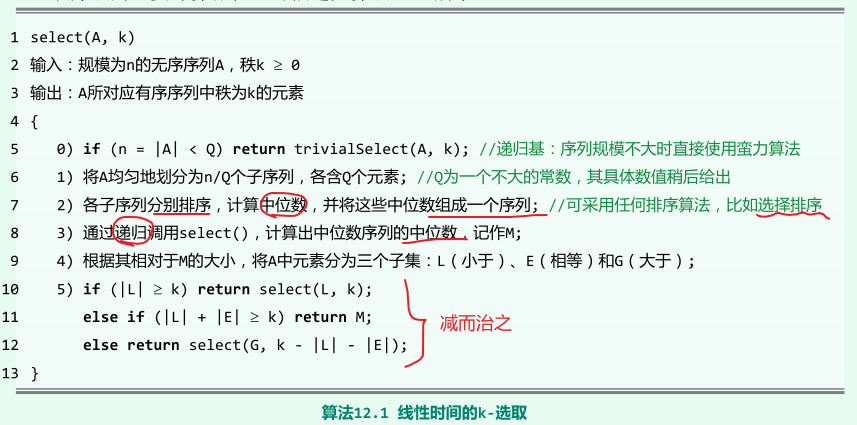
  • k-选取目标元素所处位置的三种可能情况

  

  • 复杂度

    • 算法的第5)步尽管会发生递归，但需进一步处理的序列的规模，绝不致超过原序列的3/4；

    • T(n) = cn + T(n/Q) + T(3n/4)；若取Q = 5，则有

      T(n) = cn + T(n/5) + T(3n/4) = O(20cn) = O(n)

    • 线性复杂度中的常系数项过大，以致在通常规模的应用中难以体现出优势；

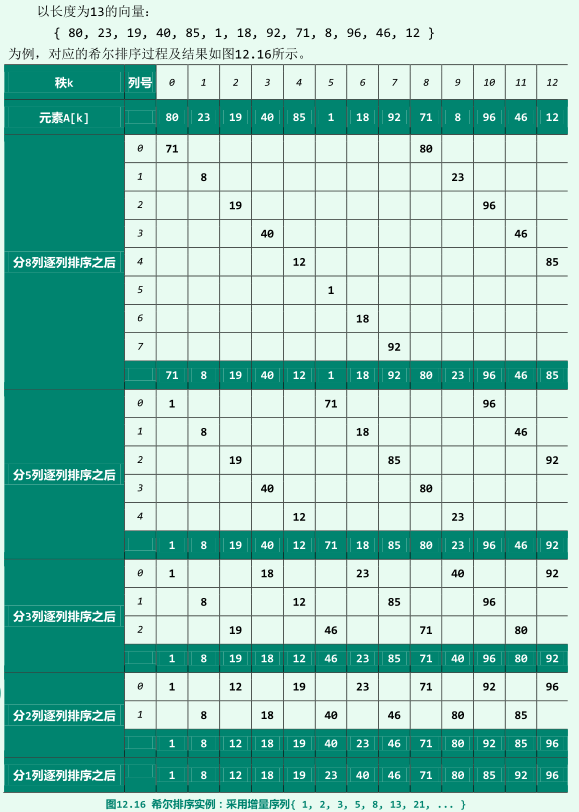
希尔排序

• 递减增量策略

  • 希尔排序（Shellsort）算法将整个待排序向量A[ ]等效地视作一个二维矩阵B[ ] [][][][][][][ ]

    

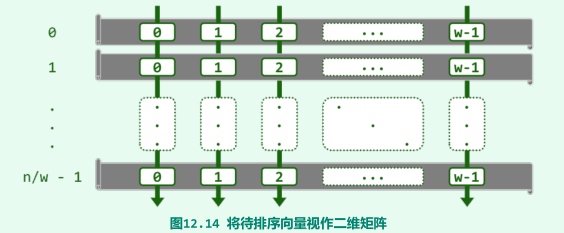
  • 若原一维向量为A[0, n)，则对于任一固定的矩阵宽度w，A与B中元素之间总有一一对应关系:

    • B[i] [j] = A[iw + j]
    • A[k] = B[k / w] [k % w]

  • 算法框架

    

  • 希尔排序是个迭代式重复的过程，各步迭代中矩阵的宽度呈缩减的趋势，直至最终使用w_1 = 1；

  • 支持希尔排序的底层排序算法，必须是输入敏感的，这样才会在每步迭代中减小逆序对数目；

  

• 增量序列

  • 理论：

    • 已经g-有序的向量，再经h-排序之后，依然保持g-有序，对于g和h的任一线性组合mg + nh，该向量也应(mg + nh)-有序；
    • 必须尽可能减少不同增量值之间的公共因子，至少保证相邻项之间应彼此互素，只要g和h互素，逆序对的间距就绝不可能大于(g - 1)∙(h - 1)；
    • 希尔排序过程中向量中每个元素所能参与构成的逆序对持续减少，整个向量所含逆序对的总数也持续减少，底层所采用的插入排序算法的实际执行时间，也将不断减少，从而提高希尔排序的整体效率。

  • Shell序列

    

    • 由于除首项外均可被2整除，故最后一次迭代前，两个子序列之间有序性并无改善，导致最后一轮插入排序所做比较操作次数共计O(n^2)；

  • Papernov-Stasevic序列

    

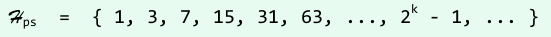
    • 在最坏情况下的运行时间不超过O(n^(3/2))；

  • Pratt序列

    

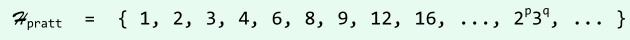
    • 在最坏情况下的运行时间不超过O(nlog^2_n)，但其中各项的间距太小，会导致迭代趟数过多；

  • Sedgewick序列

    

    • 在最坏情况下的时间复杂度为O(n^(4/3))，平均复杂度为O(n ^(7/6))，在通常的应用环境中，这一增量序列的综合效率最佳。