AGA8压缩因子算法C语言

一.AGA8算法概述

工作状态下的压缩因子是天然气最重要的物性参数之一，涉及到天然气的勘探、开发、输送、计量和利用等各个方面。实测天然气压缩因子所需的仪器设备价格高，不易推广，因此计算方法发展很快，主要为经验公式和状态方程计算方法。1992年6月26日，国际标准化组织(ISO)天然气技术委员会(TC193)及分析技术分委员会(TC193/SC1)在挪威斯泰万格(Stavanger)召开了第四次全体会议，会上推荐了两个精度较高的计算工作状态下天然气压缩因子的方程，目PAGA8-92DC方程、SGERG-88方程[1]。随后，国际标准化组织于1994年形成了国际标准草案[2]。
AGA8-92DC方程来自美国煤气协会(AGA)。美国煤气协会在天然气压缩因子和超压缩因子表的基础上，开展了大量研究，于1992年发表了以状态方程为基础计算压缩因子的AGA No.8报告及AGA8-92DC方程[2]。

二.2AGA8—92DC方法的计算过程

1.已知条件

a)绝对压力P、热力学温度T、组分数N；
b)各组分的摩尔分数Xi，i = 1～N ；
c)可查GB／T 17747．2附录B中表B1、B2、B3得到的数据：
58种物质的状态方程参数an,bn,cn,kn,un,gn,qn,fn,sn,wn；
21种识别组分的特征参数Mi，Ei，Ki，Gi，Qi，Fi，Si , Wi；
21种识别组分的二元交互作用参数Eij*，Uij，Kij，Gij 。

2.待求量

压缩因子 Z 。

3.计算步骤

a)计算第二维利系数B(1个值)；
b)计算系数Cn*，n = 13～58，共46个值；
c)计算混合物体积参数K(1个值)；
d)形成压力的状态方程；
e)解压力的状态方程，求得压缩因子Z 。

三.求解公式

1.计算第二维利系数B

二元参数Eij，Gij的计算式为：


Bnij*的计算公式为：

B按照下式计算：

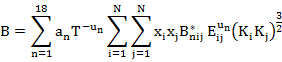
2.计算系数Cn

由下式计算：

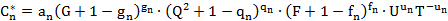
式（5）中的U,G,Q,F只与天然气的组成有关，按下式计算：

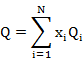
3.计算混合物体积参数K

4.形成压力的状态方程

整理得：

令：




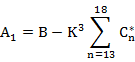
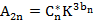
则上式变形为(式14)：

5.解方程，求得压缩因子Z

方程曲线的形状：
将上式14左边用f(pm)表示，通过计算，得到若干(pm,f(pm))数对，进行描点，得到方程曲线的形状，见下图。

求解方法的确定：
式（14）是一个超越方程，求解方法有二分法、牛顿法、近似牛顿法等。经分析，方程解的区间可以确定，采用二分法比较简捷。
求解步骤：
1)给出方程解的区间（a,b）
对一般的p、T条件，Z必然处于0.45和1.2之间。因此，取：


2)对有根区间取中值c=(a+b)/2,计算f(pm)的值f©
由上述系列公式可得：

令：Pcal=cZRT
式中Pcal----由Z得出的压力的计算值，MPa
若|P-Pcal|<1.0*e-6，则达到精度，输出Z，计算结束；否则，继续下一步3)。
3)若f©>0，则将c赋值给b ；否则，将c赋值给a 。
转向步骤2) 。

四.程序源码

/*AGA8_table文件：存储一些固定参数*/
#ifndef __AGA8_TABLE_H
#define __AGA8_TABLE_H
//58种物质的状态方程参数，an,un,bn,cn,kn,gn,qn,fn,sn,wn
double  an[58] = { 0.1538326,1.341953,-2.998583,-0.04831228,0.3757965,-1.589575,-0.05358847,0.886594630,-0.71023704,-1.471722,1.32185035,-0.78665925,2.29129e-9,0.1576724,-0.4363864,-0.04408159,-0.003433888,0.03205905,0.02487355,0.07332279,-0.001600573,0.6424706,-0.4162601,-0.06689957,0.2791795,-0.6966051,-0.002860589,-0.008098836,3.150547,0.007224479,-0.7057529,0.5349792,-0.07931491,-1.418465,-5.99905e-17,0.1058402,0.03431729,-0.007022847,0.02495587,0.04296818,0.7465453,-0.2919613,7.294616,-9.936757,-0.005399808,-0.2432567,0.04987016,0.003733797,1.874951,0.002168144,-0.6587164,0.000205518,0.009776195,-0.02048708,0.01557322,0.006862415,-0.001226752,0.002850908 };//an
double  un[58] = { 0.0,0.5,1.0,3.5,-0.5,4.5,0.5,7.5,9.5,6.0,12.0,12.5,-6.0,2.0,3.0,2.0,2.0,11.0,-0.5,0.5,0,4,6,21,23,22,-1,-0.5,7,-1,6,4,1,9,-13,21,8,-0.5,0,2,7,9,22,23,1,9,3,8,23,1.5,5,-0.5,4,7,3,0,1,0 };//un
int bn[58] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 7, 7, 8, 8, 8, 9, 9 };//bn
int cn[58] = { 0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,0,1,1,1,1,0,1,0,1,1,1,1,1,1 };//cn
int kn[58] = { 0,0,0,0,0,0,0,0,0,0,0,0,3,2,2,2,4,4,0,0,2,2,2,4,4,4,4,0,1,1,2,2,3,3,4,4,4,0,0,2,2,2,4,4,0,2,2,4,4,0,2,0,2,1,2,2,2,2 };//kn
int gn[58] = { 0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0,0 };//gn
int qn[58] = { 0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,0,1 };//qn
int fn[58] = { 0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };//fn
int sn[58] = { 0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };//sn
int wn[58] = { 0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };//wn
//21种识别组分的特种参数Mi,Ei,Ki,Gi,Qi,Fi,Si,Wi
double Mi[21] = { 16.043, 28.0135, 44.01, 30.07, 44.097, 18.0153, 34.082, 2.0159, 28.01, 31.9988, 58.123, 58.123, 72.15, 72.15, 86.177, 100.204, 114.231, 128.258, 142.285, 4.0026, 39.948 };//Mi
double Ei[21] = { 151.3183,99.73778,241.9606,244.1667,298.1183,514.0156,296.355,26.95794,105.5348,122.7667,324.0689,337.6389,365.5999,370.6823,402.636293,427.72263,450.325022,470.840891,489.558373,2.610111,119.6299 };//Ei
double Ki[21] = { 0.4619255,0.4479153,0.4557489,0.5279209,0.583749,0.3825868,0.4618263,0.3514916,0.4533894,0.4186954,0.6406937,0.6341423,0.6738577,0.6798307,0.7175118,0.7525189,0.784955,0.8152731,0.8437826,0.3589888,0.4216551 };//Ki
double Gi[21] = { 0,0.027815,0.189065,0.0793,0.141239,0.3325,0.0885,0.034369,0.038953,0.021,0.256692,0.281835,0.332267,0.366911,0.289731,0.337542,0.383381,0.427354,0.469659,0,0 };//Gi
double Qi[21] = { 0,0,0.69,0,0,1.06775,0.633276,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };//Qi
double Fi[21] = { 0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0 };                //Fi
double Si[21] = { 0,0,0,0,0,1.5822,0.39,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };        //Si
double Wi[21] = { 0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 };                //Wi
//21种识别组分的二元交互作用参数Eij,Uij,Kij,Gij   
double EE[21][21] = {
	{1,0.971640,0.960644,1,0.994635,0.708218,0.931484,1.170520,0.990126,1,1.019530,0.989844,1.002350,0.999268,1.107274,0.880880,0.880973,0.881067,0.881161,1,1},//1
	{0.971640,1,1.022740,0.970120,0.945939,0.746954,0.902271,1.086320,1.005710,1.021000,0.946914,0.973384,0.959340,0.945520,1,1,1,1,1,1,1},//2
	{0.960644,1.022740,1,0.925053,0.960237,0.849408,0.955052,1.281790,1.500000,1,0.906849,0.897362,0.726255,0.859764,0.855134,0.831229,0.808310,0.786323,0.765171,1,1},//3
	{1,0.970120,0.925053,1,1.022560,0.693168,0.946871,1.164460,1,1,1,1.013060,1,1.005320,1,1,1,1,1,1,1},//4
	{0.994635,0.945939,0.960237,1.022560,1,1,1,1.034787,1,1,1,1.004900,1,1,1,1,1,1,1,1,1},//5
	{0.708218,0.746954,0.849408,0.693168,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//6
	{0.931484,0.902271,0.955052,0.946871,1,1,1,1,1,1,1,1,1,1,1.008692,1.010126,1.011501,1.012821,1.014089,1,1},//7
	{1.170520,1.086320,1.281790,1.164460,1.034787,1,1,1,1.100000,1,1.300000,1.300000,1,1,1,1,1,1,1,1,1},//8
	{0.990126,1.005710,1.500000,1,1,1,1,1.100000,1,1,1,1,1,1,1,1,1,1,1,1,1},//9
	{1,1.021000,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//10
	{1.019530,0.946914,0.906849,1,1,1,1,1.300000,1,1,1,1,1,1,1,1,1,1,1,1,1},//11
	{0.989844,0.973384,0.897362,1.013060,1.004900,1,1,1.300000,1,1,1,1,1,1,1,1,1,1,1,1,1},//12
	{1.002350,0.959340,0.726255,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//13
	{0.999268,0.945520,0.859764,1.005320,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//14
	{1.107274,1,0.855134,1,1,1,1.008692,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//15
	{0.880880,1,0.831229,1,1,1,1.010126,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//16
	{0.880973,1,0.808310,1,1,1,1.011501,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//17
	{0.881067,1,0.786323,1,1,1,1.012821,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//18
	{0.881161,1,0.765171,1,1,1,1.014089,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//19
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//20
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1} };//21
double U[21][21] = {
	{1,0.886106,0.963827,1,0.990877,1,0.736833,1.15639,1,1,1,0.992291,1,1.00367,1.302576,1.191904,1.205769,1.219634,1.233498,1,1},//1
	{0.886106,1,0.835058,0.816431,0.915502,1,0.993476,0.408838,1,1,1,0.993556,1,1,1,1,1,1,1,1,1},//2
	{0.963827,0.835058,1,0.96987,1,1,1.04529,1,0.9,1,1,1,1,1,1.06638,1.077634,1.088178,1.098291,1.108021,1,1},//3
	{0.990877,0.816431,0.96987,1,1.065173,1,0.971926,1.61666,1,1,1.25,1.25,1.25,1.25,1,1,1,1,1,1,1},//4
	{0.990877,0.915502,1,1.065173,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//5
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//6
	{0.736833,0.993476,1.04529,0.971926,1,1,1,1,1,1,1,1,1,1,1.028973,1.033754,1.038338,1.042735,1.046966,1,1},//7
	{1.15639,0.408838,1,1.61666,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//8
	{1,1,0.9,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//9
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//10
	{1,1,1,1.25,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//11
	{0.992291,0.993556,1,1.25,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//12
	{1,1,1,1.25,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//13
	{1.00367,1,1,1.25,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//14
	{1.302576,1,1.06638,1,1,1,1.028973,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//15
	{1.191904,1,1.077634,1,1,1,1.033754,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//16
	{1.205769,1,1.088178,1,1,1,1.038338,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//17
	{1.219634,1,1.098291,1,1,1,1.042735,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//18
	{1.233498,1,1.108021,1,1,1,1.046966,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//19
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//20
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//21
};
double K[21][21] = {
	{1,1.00363,0.995933,1,1.007619,1,1.00008,1.02326,1,1,1,0.997596,1,1.002529,0.982962,0.983565,0.982707,0.981848,0.980991,1,1},//1
	{1.00363,1,0.982361,1.00796,1,1,0.942596,1.03227,1,1,1,1,1,1,1,1,1,1,1,1,1},//2
	{0.995933,0.982361,1,1.00851,1,1,1.00779,1,1,1,1,1,1,1,0.910183,0.895362,0.881152,0.86752,0.854406,1,1},//3
	{1,1.00796,1.00851,1,0.986893,1,0.999969,1.02034,1,1,1,1,1,1,1,1,1,1,1,1,1},//4
	{1.007619,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//5
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//6
	{1.00008,0.942596,1.00779,0.999969,1,1,1,1,1,1,1,1,1,1,0.96813,0.96287,0.957828,0.952441,0.948338,1,1},//7
	{1.02326,1.03227,1,1.02034,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//8
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//9
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//10
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//11
	{0.997596,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//12
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//13
	{1.002529,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//14
	{0.982962,1,0.910183,1,1,1,0.96813,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//15
	{0.983565,1,0.895362,1,1,1,0.96287,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//16
	{0.982707,1,0.881152,1,1,1,0.957828,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//17
	{0.981848,1,0.86752,1,1,1,0.952441,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//18
	{0.980991,1,0.854406,1,1,1,0.948338,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//19
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//20
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//21
};
double GG[21][21] = {
	{1,1,0.807653,1,1,1,1,1.95731,1,1,1,1,1,1,1,1,1,1,1,1,1},//1
	{1,1,0.982746,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//2
	{0.807653,0.982746,1,0.370296,1,1.67309,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//3
	{1,1,0.370296,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//4
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//5
	{1,1,1.67309,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//6
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//7
	{1.95731,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//8
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//9
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//10
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//11
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//12
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//13
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//14
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//15
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//16
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//17
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//18
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//19
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//20
	{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1},//21
};
/*下为国标上给出的六种气体组分*/
double table3[6][17] = {
	{0.965,0.003,0.006,0.018,0.0045,0,0,0,0,0,0.001,0.001,0.0005,0.0003,0.0007,0,0},//1
	{0.907,0.031,0.005,0.045,0.0084,0,0,0,0,0,0.001,0.0015,0.0003,0.0004,0.0004,0,0},//2
	{0.859,0.01,0.015,0.085,0.023,0,0,0,0,0,0.0035,0.0035,0.0005,0.0005,0,0,0},//3
	{0.735,0.1,0.016,0.033,0.0074,0,0,0.095,0.01,0,0.0012,0.0012,0.0004,0.0004,0.0002,0.0001,0.0001},//4
	{0.812,0.057,0.076,0.043,0.009,0,0,0,0,0,0.0015,0.0015,0,0,0,0,0},//5
	{0.826,0.117,0.011,0.035,0.0075,0,0,0,0,0,0.0012,0.0012,0.0004,0.0004,0.0002,0.0001,0},//6
};
#endif 

/*AGA8.h文件：声明一些函数及变量*/
#ifndef __AGA8_H
#define __AGA8_H
#define NUM 17                         //定义当前气体组分数

typedef  unsigned char u8;             //定义u8
typedef  unsigned short int u16;       //定义u16
typedef  unsigned int u32;             //定义u32

#define R  8.31451e-3                  //定义气体常数
constexpr auto TT = 280;               //定义绝对温度
constexpr auto P = 12;                  //定义绝对压力

void Caculate_fix_parameter(void);    //计算获得固定参数，只需要计算一次（执行前）
void Caculate_x_parameter(void);      //计算获得与输入气体组分X有关的参数，只需要计算一次（执行中）
double f_pm(double pm);              //形成压力的状态方程
/***********************************计算与X组分相关的参数数组**************************************/
extern double X[NUM];                  //外部声明X
extern double X_SQUARE[NUM];           //外部声明X平方计算结果
extern double XIXI[NUM][NUM];          //外部声明XIXI计算结果
extern double XIXJ[NUM][NUM];          //外部声明XIXJ计算结果
void X_Caculate(double x[]);                   //定义与输入的相关组分的X的计算函数
/***********************************第一步：计算第二维利系数B(1个值)**************************************/
extern double B_parameter[NUM][NUM];          //外部声明第二维利系数B参数计算结果
void B_Caculate_parameter(void);              //声明第二维利系数B参数计算函数
double B_Caculate(void);                      //第一步：计算第二维利系数B(1个值)
/***********************************第二步：计算系数Cn，n = 13～58，共46个值**************************************/
extern double G_parameter[NUM][NUM];
extern double U_parameter[NUM][NUM];
extern double E_parameter[NUM];
extern double T_parameter[58];
void Cn_Caculate_parameter(void);           //计算与Cn有关的固定参数
double Cn_Caculate(u8 n);                   //计算Cn，与X有关
/***********************************第三步：计算混合物体积参数K(1个值)**************************************/
extern double K_parameter[NUM][NUM];
extern double KK_parameter[NUM];
void K_Caculate_parameter(void);          //计算与K有关的固定参数
double K_Caculate(void);                  //计算K，与X有关
/***********************************第四步：计算压力的状态方程的预先参数**************************************/
extern double K1;
extern double A1;
extern double PM_parameter;
extern double A2_parameter[58];
extern double A3_parameter[58];
extern double A4_parameter[58];
void FPM_Caculate(void);            //计算压力的状态方程的预先参数

#endif

/*AGA8.c文件：定义一些函数及变量*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include "AGA8.h"
#include "AGA8_table.h"
/****************************************计算获得固定参数，只需要计算一次（执行前）*************************************************/
void Caculate_fix_parameter(void)
{
	B_Caculate_parameter();               //1.计算与B的相关固定系数
	Cn_Caculate_parameter();              //2.计算与Cn有关的固定参数
	K_Caculate_parameter();               //3.计算与K有关的固定参数
}
/****************************************计算获得与输入气体组分X有关的参数，只需要计算一次（执行中）*******************************/
double K1 = 0;
double A1 = 0;
void Caculate_x_parameter(void)              
{
	int n, i;
	double x[17] = { 0 };                        //定义数组x缓存区用于存放被测气体组分
	for (i = 0; i < 17; i++)
		x[i] = table3[5][i];                     //将表格中数据放到x缓存区中
	X_Caculate(x);                               //0.计算得出气体组分相关参数                     
	double B1 = B_Caculate();                    //1.计算出第二维利系数B(1个值)
	K1 = K_Caculate();                           //3.计算出混合物体积参数K
	for (n = 12; n < 18; n++)
		A1 = A1 + Cn_Caculate(n);                //2.计算系数Cn
	A1 = B1 - K1*K1*K1*A1;
	FPM_Caculate();                              //4.计算压力的状态方程的预先参数
}
/***************************************形成压力的状态方程****************************************************/
double f_pm(double pm)
{
	int n;
	double f_pm = pm + A1 * pm*pm + PM_parameter;
	for (n = 12; n < 58; n++)
		f_pm = f_pm + pm * A2_parameter[n]*(bn[n] - A3_parameter[n] * pow(pm, kn[n]))*pow(pm, bn[n])*exp(A4_parameter[n]*pow(pm,kn[n]));
	return f_pm;
};
/***********************************第0步:计算与X组分相关的参数数组**************************************/
double X[NUM] = { 0 };                  //定义X平方计算结果
double X_SQUARE[NUM] = { 0 };           //定义X平方计算结果
double XIXI[NUM][NUM] = { 0 };          //定义XIXI计算结果
double XIXJ[NUM][NUM] = { 0 };          //定义XIXJ计算结果
void X_Caculate(double x[])                    //定义与输入的相关组分的X的计算函数
{
	u8 i, j;
	for (i = 0; i < NUM; i++)
	{
		X[i] = x[i];
		X_SQUARE[i] = x[i] * x[i];             //计算得出X平方计算结果
	}
	for (i = 0; i < NUM; i++)
		for (j = 0; j < NUM; j++)
			XIXI[i][j] = x[i] * x[j];          //计算得出XIXI计算结果
	for (i = 0; i < NUM - 1; i++)
		for (j = i + 1; j < NUM; j++)
			XIXJ[i][j] = x[i] * x[j];          //计算得出XIXJ计算结果
}
/***********************************第1步：计算第二维利系数B(1个值)**************************************/
/*计算思想是：把累加符号调换位置*/
double B_parameter[NUM][NUM] = { 0 };          //定义第二维利系数B参数计算结果
void B_Caculate_parameter(void)                //计算与B有关的固定参数
{
	u8 i, j, n;
	double G[21][21];
	double B_n[21][21];
	double E_n[21][21];
	double K[21][21];
	for (i = 0; i < NUM; i++)
		for (j = 0; j < NUM; j++)
		{
			for (n = 0; n < 18; n++)
			{
				G[i][j] = (GG[i][j] * (Gi[i] + Gi[j])) / 2;
				B_n[i][j] = (pow((G[i][j] + 1 - gn[n]), gn[n]))*(pow((Qi[i] * Qi[j] + 1 - qn[n]), qn[n]))*(pow((pow(Fi[i], 0.5) * pow(Fi[j], 0.5) + 1 - fn[n]), fn[n]))*(pow((Si[i] * Si[j] + 1 - sn[n]), sn[n]))*(pow((Wi[i] * Wi[j] + 1 - wn[n]), wn[n]));
				E_n[i][j] = pow(EE[i][j] * pow(Ei[i] * Ei[j], 0.5), un[n]);
				K[i][j] = pow(Ki[i] * Ki[j], 1.5);
				B_parameter[i][j] = B_parameter[i][j] + an[n] * (pow(TT, -un[n]))*B_n[i][j] * E_n[i][j] * K[i][j];
			}
		}
}
//计算第二维利系数B(1个值)，与X有关
double B_Caculate(void)        //计算B，与X有关
{
	u8 i, j;
	double B_total = 0;
	for (i = 0; i < NUM; i++)
		for (j = 0; j < NUM; j++)
			B_total = B_total + XIXI[i][j] * B_parameter[i][j];
	return B_total;
}
/***********************************第2步：计算系数Cn，n = 13～58，共46个值**************************************/
double G_parameter[NUM][NUM] = { 0 };
double U_parameter[NUM][NUM] = { 0 };
double E_parameter[NUM] = { 0 };
double T_parameter[58] = { 0 };
void Cn_Caculate_parameter(void)  //计算与Cn有关的固定参数
{
	int i = 0, j = 0;
	for (i = 0; i < NUM - 1; i++)
		for (j = i + 1; j < NUM; j++)
		{
			G_parameter[i][j] = (GG[i][j] - 1)*(Gi[i] + Gi[j]);
			U_parameter[i][j] = 2 * (pow(U[i][j], 5) - 1)*pow(Ei[i] * Ei[j], 2.5);
		}
	for (i = 0; i < NUM; i++)
		E_parameter[i] = pow(Ei[i], 2.5);
	for (i = 12; i < 58; i++)
		T_parameter[i] = an[i] * pow(TT, -un[i]);
}
double Cn_Caculate(u8 n)        //计算Cn，与X有关
{
	int i = 0, j = 0;
	double G = 0, Q = 0, F = 0, U_5 = 0, U = 0, Cn=0;
	for (i = 0; i < NUM - 1; i++)
		for (j = i + 1; j < NUM; j++)
		{
			G = G + XIXJ[i][j] * G_parameter[i][j];
			U_5 = U_5 + XIXJ[i][j] * U_parameter[i][j];
		}
	for (i = 0; i < NUM; i++)
	{
		G = G + X[i] * Gi[i];       //求出G
		Q = Q + X[i] * Qi[i];       //求出Q
		F = F + X_SQUARE[i] * Fi[i];//求出F
		U = U + X[i] * E_parameter[i];
	}
	U = pow(U * U+ U_5,0.2);               //求出U
	Cn = pow(G + 1 - gn[n], gn[n])*pow(Q*Q + 1 - qn[n], qn[n])*pow(F + 1 - fn[n], fn[n])*pow(U, un[n])*T_parameter[n];
	return Cn;
}
/***********************************第3步：计算混合物体积参数K(1个值)**************************************/
double K_parameter[NUM][NUM] = { 0 };
double KK_parameter[NUM] = { 0 };
void K_Caculate_parameter(void)  //计算与K有关的固定参数
{
	int i = 0, j = 0;
	for (i = 0; i < NUM - 1; i++)
		for (j = i + 1; j < NUM; j++)
			K_parameter[i][j] = 2 * (pow(K[i][j], 5) - 1)*pow(Ki[i] * Ki[j], 2.5);
	for (i = 0; i < NUM; i++)
			KK_parameter[i] = pow(Ki[i], 2.5);
}
double K_Caculate(void)        //计算K，与X有关
{
	int i = 0, j = 0;
	double K_5 = 0;
	for (i = 0; i < NUM; i++)
		K_5 = K_5 + X[i] * KK_parameter[i];
	K_5 = K_5 * K_5;
	for (i = 0; i < NUM - 1; i++)
		for (j = i + 1; j < NUM; j++)
			K_5 = K_5 + XIXJ[i][j] * K_parameter[i][j];
	K_5 = pow(K_5, 0.2);
	return K_5;
}
/***********************************第4步：计算压力的状态方程的预先参数**************************************/
double PM_parameter = 0;
double A2_parameter[58] = { 0 };
double A3_parameter[58] = { 0 };
double A4_parameter[58] = { 0 };
void FPM_Caculate(void)            //计算压力的状态方程的预先参数
{
	u8 i = 0;
	PM_parameter= - P / (R*TT);
	for (i = 12; i < 58; i++)
	{
		A2_parameter[i] = Cn_Caculate(i)*pow(K1, 3 * bn[i]);
		A3_parameter[i] = cn[i] * kn[i] * pow(K1, 3 * kn[i]);
		A4_parameter[i] = -cn[i] * pow(K1, 3 * kn[i]);
	}
}

//main.c文件：调用函数，计算输出压缩因子Z
#include <stdio.h>
#include <stdlib.h>
#include<time.h>            //为了支持clock()函数
#include "AGA8.h"
int main()
{
		int k = 0;
		Caculate_fix_parameter();          //计算获得固定参数，只需要计算一次（执行前）
		double a = 0.833*P / (R*TT), b = 2.5*P / (R*TT), c, f_c, Z, Pcal;
		long start_time = clock();         //获取此程序段开始执行时间
		Caculate_x_parameter();            //计算获得与输入气体组分X有关的参数，只需要计算一次（执行中）
	mark:c = (a + b) / 2;
		f_c = f_pm(c);
		Z = (f_c + P / (R*TT)) / c;
		Pcal = c * Z*R*TT;
		k += 1;
		if (P - Pcal > -1e-6 && P - Pcal < 1e-6)//满足条件，循环结束
		{
			printf("Z=%.15lf\n", P / (c*R*TT));
			printf("k=%d\n", k);
		}
		else
		{
			if (f_c > 0)
				b = c;
			else a = c;
			goto mark;
		}
		long end_time = clock();        //获取此程序段开始执行时间
		long t = end_time - start_time; //获取程序执行时间
		printf("clock run time is:%d ms\n", t);  //输出时间
		system("pause");
		return 0;
};

五. 感谢支持

    完结撒花！AGA8算法原理上不难理解，但是实现上还是相当复杂的，尤其是好几个国标表达还不一致，只能自己从中去找问题。因此写这篇文章花了我很大精力，遇到了无数问题，个个都让人头大。也感谢开源小伙伴提供的代码，分析和思考，给了我很大帮助。希望看到这里的小伙伴能点个关注，我后续会持续更新，也欢迎大家广泛交流。
    码字实属不易，如果本文对你有10分帮助，就赏个10分把，感谢各位大佬支持！