目录
1. 控制体表面应力张量
控制体x方向表面压力可见图:
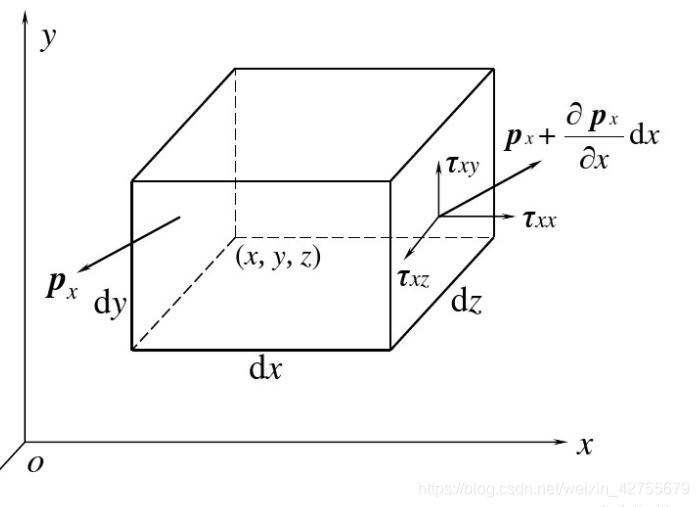
那么作用于单位体积流体的表面压力为:

注意,这里Px, Py, Pz均为向量。则其可分解为:

其中,第一个下标代表应力所在平面的外法线方向,第二个下标代表应力方向。这里,为了描述微元上的应力,将应力张量表示为:
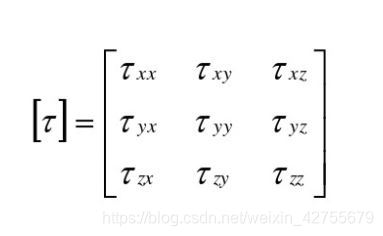
则外法线单位矢量 方向上的表面应力(压力)为:
则单位体积流体的表面力为:
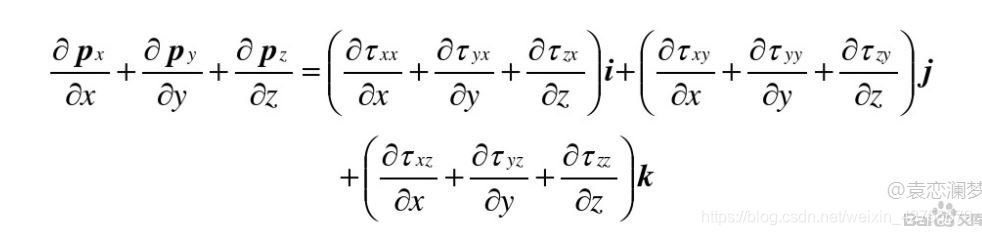
2. 应变率张量与亥姆霍兹速度分解定理
将速度增量沿三个方向分解得
将系数矩阵进行分解得
令
,
,
称E为流体的应变率张量或变形速率张量, 为流体的转动角速度矢量,则:
其三项分别对应M点平动速度、流体变形速度、绕M中心圆转速度。
关于矩阵 和
,从物理上解释,有:
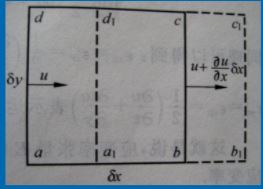
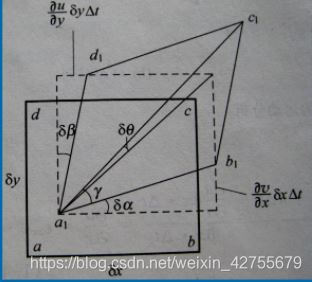
为相对伸长率;
为平均角变形率,诸如此类推。
则,微团体积相对膨胀率可推得为, 而对于不可压缩流体,体积膨胀率为0。
为流体微元旋转角速度。对于无旋流动,
。
3. 流体的本构方程——应力张量与变形率张量的一般线性关系
应力与变形速率之间存在线性关系,服从这种线性关系的流体称为牛顿流体。其满足牛顿内摩擦定律。
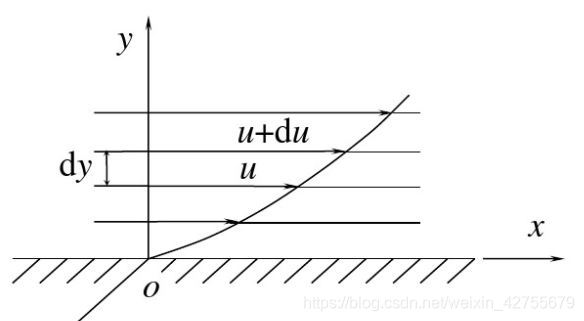
在边界层内,垂直板方向速度为0,则
斯托克斯将牛顿内摩擦定律进行推广,即假设
1. 流体连续,其应力张量是变形率张量的线性函数。
2. 流体是各向同性的,即它的性质与方向无关。无论坐标系如何选取,它的应力与变形率的关系是相同的。
3. 当流体静止,即变形率为零,流体中应力就是流体静压力。
之前我们知道:

对于静止流体与运动的无粘流体,不存在切应力分量,则:
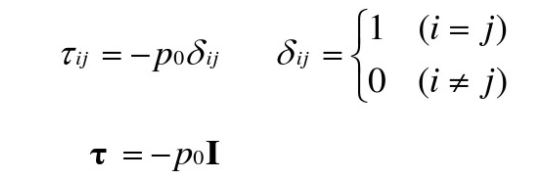
负号代表压力方向与微元外表面方向相反。
根据应力张量与变形率张量是线性关系和各向同性假设,应力张量和变形率张量可以写成:
![]()
参照牛顿内摩擦定律,认为 。对于系数b,由于b为标量,它应该由张量
和
的分量中的坐标转换时不变的值组成。对于张量,取其第一不变量(即矩阵的迹)。
![]()
带入上式,则:
![]()
左式的迹与右式的迹相等,则:
![]()
![]()
静止情况下, 值为零,且
,代入上式有:
![]()
使得上式恒成立,有,
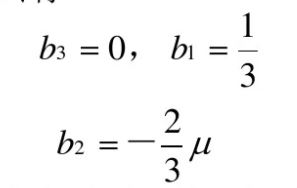
则可认为应力张量与变形率张量之间存在一般线性关系:、
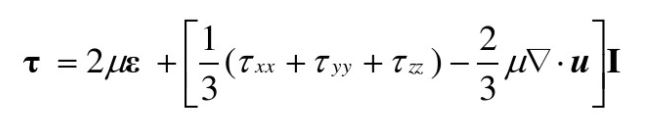
引入平均压强的概念,其一点的压强在各个方向是相等的,其值即为平均法向应力,有:
![]()
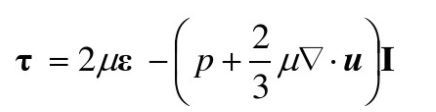
令,成之为膨胀粘性系数,有:
![]()
若以 和
代表速度和位移在 x,y,z 方向的分量,有:
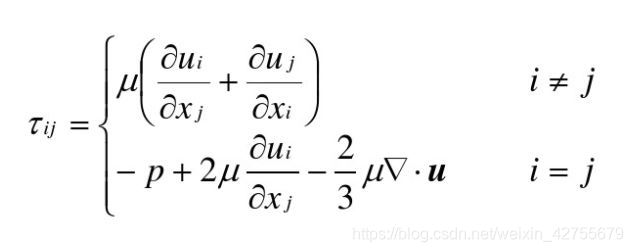
即为可压缩流体的本构方程。虽然公式推导使用了不严格的假定,但其已经被实验广泛证实。
本文内容基本均来源于两个PPT:
https://wenku.baidu.com/view/f5f45506783e0912a3162a45.html
https://max.book118.com/html/2018/0526/168864127.shtm
前者较为通俗易懂,后者则给出了应力张量和应变率张量的详细讨论。如本文有何错误,欢迎指正,谢谢。








 本文介绍了流体力学中的关键概念,包括控制体表面应力张量、应变率张量及其与亥姆霍兹速度分解定理的关系,以及流体的本构方程。深入探讨了应力张量与变形率张量之间的线性关系。
本文介绍了流体力学中的关键概念,包括控制体表面应力张量、应变率张量及其与亥姆霍兹速度分解定理的关系,以及流体的本构方程。深入探讨了应力张量与变形率张量之间的线性关系。
















 1697
1697

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








