完美涡旋光束及其代码实现

NeverComplacent

已于 2023-11-29 23:39:59 修改

阅读量3.1k

点赞数 22

分类专栏：光学OAM 文章标签：人工智能

于 2023-11-29 23:36:54 首次发布

本文链接：https://blog.csdn.net/weixin_42764222/article/details/134701725

版权

光学OAM 专栏收录该内容

2 篇文章

订阅专栏

一、完美涡旋光束

1、完美涡旋光束概念

传统方法产生的涡旋光其光束半径会随拓扑荷数的增加而增加。为了满足涡旋光在传输、耦合时光束半径不宜过大的条件，迫切需要研究一种光束半径与拓扑荷数无关的涡旋光束。

美涡旋光场具有光束横截面半径不随拓扑荷值改变而改变的优点，在量子物理、量子操控、光学超分辨成像及量子通信等领域具有深远影响和重要地位。

目前，最常用的完美涡旋产生方法是利用锥透镜产生完美涡旋光场。2014年，Ostrovsky等人在此之前的研究基础上，利用了Bessel函数截断法，提出了一种既可以保证高质量又简化实验装置的实验方法。

2、完美涡旋光束原理

产生完美涡旋光是基本原理如下。贝塞尔-高斯光束是由贝塞尔方程和高斯光束组合而来，贝塞尔高斯光束在束腰半径处的光强表达式可写为：

式中r和 $\phi$ 分别表示两个极坐标， $J_{l}$ 表示l阶贝塞尔函数的第一类函数， $k_{r}$ 表示光束的径向波矢量， $l$ 表示光束界面一周内相位变化 $2\pi$ 的次数。对上式进行傅里叶变换可得：

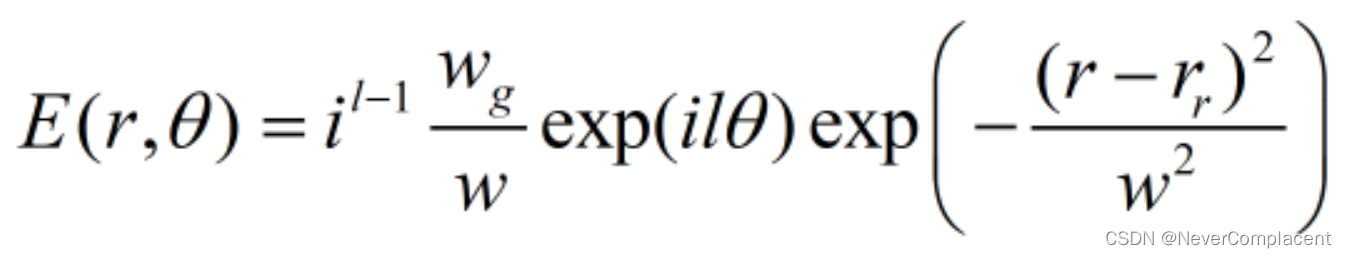
式中 $w_{z}$ 表示光斑圆环的宽度， $r_{r}$ 表示完美涡旋光的半径。在近似条件下， $r_{r}$ 的大小可由 $r_{r}=\lambda*f/d$ 来表示。

要实现以上傅里叶变换，在光学中可以通过一个傅里叶变化透镜来实现。

从以上的分析中可以看出，完美涡旋光的半径是由光波长、透镜焦距和锥透镜参数决定的，与涡旋光的拓扑荷数没有关系，其半径也可以通过相应参数来调控。

二、matlab实现

1、源代码

clc
clear all;

% Definitions
Nx = 1280; % # of pixels in x-dimension of Cambridge SLM
Ny = 1024;  % # of pixels in y-dimension of Cambridge SLM

C = ones(Ny,Nx);  %初始化

w0 = 100;  % Gaussian beam wist
w = 25;  % width of the annular ring
lamda = 633*10^-6; % wavelength
f = 10^5; %focal length
d = 0.45; % axicon parameter
l=30; % Topological charge 
A0 = 1; % Amplitude coefficient
nx = 200;
s = nx/Nx; % This parameter defines the fringe density.
phaseblaze = true;
imName='SLMpat'; % This is the name of the file that has the pattern
inName='SLMpatin';
s2s=num2str(s);

for x=1:Nx
    for y=1:Ny
        x0 = Nx/2; % coordinates of the center of the image
        y0 = Ny/2;
        xr=x-x0;
        yr=y-y0;
        r=sqrt(xr^2+yr^2); % radial coordinate
        theta=atan2(yr,xr);% + n*(pi/9) ;  % angular coordinate 可调相位角
  
        g1(y,x) = A0*(1i^(l-1))*(w0/w)*exp(1i*d*r+1i*l*theta)*exp(-(r-(lamda*f/d))^2/w^2);
        g2(y,x) = A0*(1i^(l-1))*(w0/w)*exp(1i*d*r+1i*-l*theta)*exp(-(r-(lamda*f/d))^2/w^2);
        g(y,x) = g1(y,x);%+ g2(y,x);
        
            Pg1 = g(y,x);
            % 添加闪耀光栅
            Pg2 = angle(Pg1) + 2*pi*s*xr;
            if phaseblaze % Phase blaze
                pgf = mod(Pg2,2*pi)/(2*pi); %phase mod 2 pi in units of 2pi
            else % to do binary grating
                pgf = mod(Pg2,2*pi)/(2*pi); %phase mod 2 pi in units of 2pi
                if pgf >=0.5
                    pgf=0;
                else
                    pgf=1;
                end
            end
            
         C(y,x) = pgf*118/225;                                  
    end
end

intensity=abs(g);
figure();imshow(intensity,[],'border','tight');  colormap winter;

phase=angle(g);
figure();imshow(phase,[],'border','tight');   %colormap jet;