DARTS - 论文与代码全解析

最新推荐文章于 2024-04-29 15:58:51 发布

ziwiz

最新推荐文章于 2024-04-29 15:58:51 发布

阅读量4.6k

点赞数 8

文章标签：神经网络深度学习人工智能

本文链接：https://blog.csdn.net/weixin_42765656/article/details/109598194

版权

DARTS是一种神经网络结构搜索方法，通过将结构搜索空间连续化处理，利用梯度下降算法高效搜索最优网络结构。该方法引入了混合运算，采用双参数优化策略，能够在较少计算资源下快速收敛。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

DARTS: Differentiable Architecture Search, ICLR 2019.
https://arxiv.org/pdf/1806.09055

背景

神经网络结构搜索(NAS)的原理是给定一个称为搜索空间的候选神经网络子结构集合，用某种策略从中搜索出最优的全局神经网络结构。神经网络结构的优劣即性能用某些指标如精度、速度来度量，称为性能评估。其结构可以用下图来衡量：

在每次结构搜索的迭代过程中，算法从搜索空间中选一个子结构，在训练集上训练该子网络，并在验证集上评估效果，接着通过搜索策略循环优化并找到最优的网络结构。

搜索空间定义了网络解的集合，搜索策略定义了以何种方法去寻找最优解，性能评估定义了怎样的网络结构是最优的。

传统的NAS方法大多基于强化学习(RL)或者遗传算法作为搜索的策略，基于离散的搜索空键进行黑箱优化，往往耗时巨大。

可微结构搜索

本文提出了全新的可微结构搜索算法(Differentiable Architecture Search)，将搜索空间连续化处理，便于用梯度下降等连续优化算法求解最优网络结构。

该算法提出了一个新的参数 $\alpha$ 用于表征网络结构，即该向量代表了最终网络各子结构之间的连接方式。连续结构的单次迭代分两部分：

在训练集中搜寻最优的结构参数 $\alpha$ ，并生成对应网络；
在验证集中应用该网络训练常规参数 $w$ ，并评估效果。

最后由结构参数 $\alpha$ 生成离散结构作为最终的神经网络。

Cell

DARTS中的基本结构是Cell，整个网络主体由若干Cell连接而成。Cell分为两种，Normal cell和Reduction Cell。每个同类型Cell的结构相同且共享权重，其内部由若干节点(node)组成，每个节点可以看作一个表示(representation)或者特征图(feature map)。Cell由2个输入节点，一个输出和若干中间节点组成。中间节点与前序节点(包括之前的中间节点以及2个输入节点)的连接关系可以表示为：

$x^{(j)} = \sum_{i \lt j} o^{(i,j)}(x^{(i)})$

其中 $o^{(i,j)}$ 代表某种连接关系，在CNN中，有如下备选：

# genotypes.py
PRIMITIVES = ['none', 'max_pool_3x3', 'avg_pool_3x3', 'skip_connect', 'sep_conv_3x3',
             'sep_conv_5x5', 'dil_conv_3x3', 'dil_conv_5x5']

这些操作的集合构成了操作空间 $O$ ，上述公式具体在搜索过程和测试过程中有所不同。

2个输入节点分别与前2个Cell的输出相连，中间节点与前序节点相连，所有中间节点在通道维度上的concat构成了输出节点。

搜索过程 train & validation

连续网络

对于搜索过程，中间节点与单个前序节点的连接关系可以表示为：

$\begin{aligned} \overline{o}^{(i,j)}(x) &= \sum_{o\in{O}} softmax(\alpha_o^{(i,j)}) \cdot o(x) \\ &= \sum weight^{(i,j)} \cdot o(x) \end{aligned}$

由所有在操作集中的操作加权形成mixed operation(每种操作都有一个结果，将结果加权)，其中的权重由某两节点间的结构参数 $\alpha_o^{(i,j)}$ 的 $s o f t m a x$ 生成。

每个中间节点都与其前序节点都有mixed operation的连接关系，故若一个Cell有4个中间节点，就存在 $2 + 3 + 4 + 5 = 14$ 个mixed operation。

$\alpha$ 可由二维数组表示，行索引代表Cell中的第几个mixed operation连接，列索引代表操作种类。

测试过程 test

离散网络

对于测试过程，结构参数 $\alpha$ 已经得到，需要由此确定具体的连接方式，而不是像搜索过程中用mixed operation。

中间节点与前序节点的连接关系由如下方式确定：

$x^{(j)} = \sum_{k \lt topk}max_k(weight^{(i,j)}) \cdot o_{non-zero}^{(i,j)}(x^{(i)})$

即先由 $softmax(\alpha_o^{(i,j)})$ 生成 $weight^{(i,j)}$ 向量，每个 $weight^{(i,j)}$ 都取最大的一个值并对应相关的非零操作，这样对于第 $j$ 个中间节点就得到了 $2 + j$ 个最大值，对应它的所有前序节点的某个操作，最后再取 $t o p k$ 个作为最终的连接关系。

$\begin{cases} 1, &\text{RNN} \\ 2, &\text{CNN} \end{cases}$

这样就得到了离散的最优网络结构，重新训练得到常规参数后即可用于在测试集上检验效果。

单个Cell的搜索与构建网络过程可由下图表示：

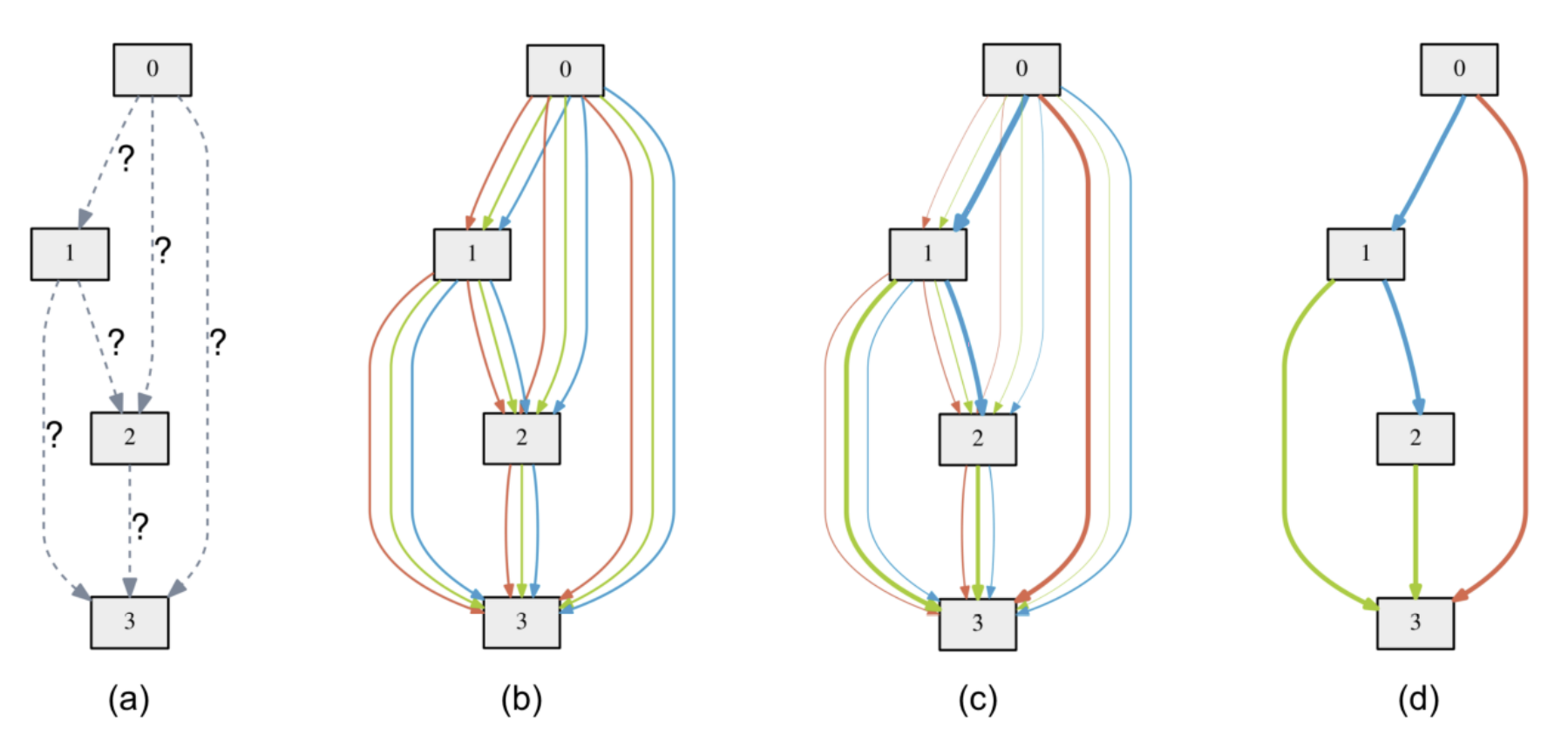
[a] 初始化各边的结构参数 $\alpha$
[b] 搜索过程的mixed operation
[c] 搜索过程的循环双参数优化
[d] 确定最终离散最优网络结构

离散结构的 Normal Cell 与 Reduction Cell (CNN)

Reduction Cell只出现在整个网络深度为1/3和2/3的位置，与输入节点连接的操作都是stride 2。

双参数优化算法

在DARTS中，因为在常规网络参数 $w$ 的基础上引入了新的结构参数 $\alpha$ ，且结构参数在训练过程中由 $s o f t m a x$ 进行的连续松弛化处理(Continuous Relaxation)，两个参数都可以用基于梯度下降的算法进行优化，故这是一个连续性的双参数优化问题：

$\begin{cases} \min_{\alpha} L_{val}(w^*(\alpha), \alpha) &(1) \\ s.t. ~~ w^*(\alpha) = \argmin_{w} L_{train}(w, \alpha) &(2) \end{cases}$

优化目标是在验证集上的 $l o s s$ 最小，也就是在当前 $\alpha$ 所对应的连续性网络中先用常规方法优化 $w$ ，然后基于此再去优化 $\alpha$ 使得 $L_{val}$ 最小。

整个优化过程分为了在训练集和在验证集上两个部分分别进行，一次循环作为一个epoch。

其中(2)式在较深的网络中耗时较长，且如果跑上几十个batch太费时间，故作者提出了一种近似的方式可以大大减少计算量。(2)式可以近似为：

$\begin{aligned} w^*(\alpha) &= \argmin_{w} L_{train}(w, \alpha) \\ & \approx w - \xi\nabla_w L_{train}(w, \alpha) \end{aligned} ~~~~~ (3)$

即只在训练集上反向传递一次 $w$ 的梯度并更新作为近似最优。(1)的优化也为反向传递一次:

$\nabla_{\alpha}L_{val}(w - \xi\nabla_w L_{train}(w, \alpha), \alpha) ~~(4)$

P.S. 代码中的(4)式叫unrolled，同时也提供了常规方法直接计算 $\nabla_{\alpha} L_{val}(w^*(\alpha), \alpha)$ .

整个搜索+验证过程可以表示为：

对于(4)式的计算，可以简化为：

$\begin{aligned} & \nabla_{\alpha}L_{val}(w - \xi\nabla_w L_{train}(w, \alpha), \alpha) \\ = & \nabla_{\alpha}L_{val}(w'(\alpha), \alpha) \\ = & \nabla_{\alpha}L_{val}(w', \alpha) \cdot 1 + \nabla_{\alpha}w'(\alpha) \cdot \nabla_{w'}L_{val}(w', \alpha) \\ = & \nabla_{\alpha}L_{val}(w', \alpha) -\xi \nabla_{\alpha, w}^2 L_{train}(w, \alpha) \cdot \nabla_{w'}L_{val}(w', \alpha) \\ \end{aligned}$

由泰勒展开：

$f(w\pm\varepsilon W) = f(w) \pm \frac{f'(w)}{1!}\varepsilon W \pm ...$

可以得到：

$\cdot W \approx \frac{f(w + \varepsilon W) - f(w - \varepsilon W)}{2\varepsilon}$

令 $\nabla_{w'}L_{val}(w', \alpha)$ ， $f(\alpha) = \nabla_wL_{train}(w, \alpha)$ ，并令 $w^{\pm} = w \pm \varepsilon\nabla_{w'}L_{val}(w', \alpha)$

则(4)式可以进一步化简为：

$\nabla_{\alpha}L_{val}(w', \alpha) - \xi \frac{\nabla_wL_{train}(w^+ , \alpha) - \nabla_wL_{train}(w^- , \alpha)}{2\varepsilon} ~~~ (5)$

由(3)式和(5)式分别对 $w$ 和 $\alpha$ 进行梯度下降优化，可以大大减少计算量。

代码解析

https://github.com/quark0/darts
Python >= 3.5.5, PyTorch == 0.3.1, torchvision == 0.2.0

一些定义

genotypes.py

# operation set in CNN.
PRIMITIVES = ['none', 'max_pool_3x3', 'avg_pool_3x3', 'skip_connect', 'sep_conv_3x3',
              'sep_conv_5x5', 'dil_conv_3x3', 'dil_conv_5x5']

# building a model from Genotype.
Genotype = namedtuple('Genotype', 'normal normal_concat reduce reduce_concat')
# each geno consists of ('op_name', index of source node).
DARTS_V2 = Genotype(normal=[('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 1), ('skip_connect', 0), ('skip_connect', 0), ('dil_conv_3x3', 2)], normal_concat=[2, 3, 4, 5], reduce=[('max_pool_3x3', 0), ('max_pool_3x3', 1), ('skip_connect', 2), ('max_pool_3x3', 1), ('max_pool_3x3', 0), ('skip_connect', 2), ('skip_connect', 2), ('max_pool_3x3', 1)], reduce_concat=[2, 3, 4, 5])

operations.py

# for BN, learnable parameters are disabled if affine is true.
# set padding to keep resolution.
OPS = {
  'none' : lambda C, stride, affine: Zero(stride),
  'avg_pool_3x3' : lambda C, stride, affine: nn.AvgPool2d(3, stride=stride, padding=1, count_include_pad=False),
  'max_pool_3x3' : lambda C, stride, affine: nn.MaxPool2d(3, stride=stride, padding=1),
  'skip_connect' : lambda C, stride, affine: Identity() if stride == 1 else FactorizedReduce(C, C, affine=affine),
  'sep_conv_3x3' : lambda C, stride, affine: SepConv(C, C, 3, stride, 1, affine=affine),
  'sep_conv_5x5' : lambda C, stride, affine: SepConv(C, C, 5, stride, 2, affine=affine),
  'sep_conv_7x7' : lambda C, stride, affine: SepConv(C, C, 7, stride, 3, affine=affine),
  'dil_conv_3x3' : lambda C, stride, affine: DilConv(C, C, 3, stride, 2, 2, affine=affine),
  'dil_conv_5x5' : lambda C, stride, affine: DilConv(C, C, 5, stride, 4, 2, affine=affine),
  'conv_7x1_1x7' : lambda C, stride, affine: nn.Sequential(
    nn.ReLU(inplace=False),
    nn.Conv2d(C, C, (1,7), stride=(1, stride), padding=(0, 3), bias=False),
    nn.Conv2d(C, C, (7,1), stride=(stride, 1), padding=(3, 0), bias=False),
    nn.BatchNorm2d(C, affine=affine)
    ),
}

# for skip_connect in reduction cell.
class FactorizedReduce(nn.Module):
  def __init__(self, C_in, C_out, affine=True):
    super(FactorizedReduce, self).__init__()
    assert C_out % 2 == 0
    self.relu = nn.ReLU(inplace=False)
    self.conv_1 = nn.Conv2d(C_in, C_out // 2, 1, stride=2, padding=0, bias=False)
    self.conv_2 = nn.Conv2d(C_in, C_out // 2, 1, stride=2, padding=0, bias=False) 
    self.bn = nn.BatchNorm2d(C_out, affine=affine)
  def forward(self, x):
    x = self.relu(x)
    out = torch.cat([self.conv_1(x), self.conv_2(x[:,:,1:,1:])], dim=1)
    out = self.bn(out)
    return out

class SepConv(nn.Module):
  def __init__(self, C_in, C_out, kernel_size, stride, padding, affine=True):
    super(SepConv, self).__init__()
    self.op = nn.Sequential(
      nn.ReLU(inplace=False),
      # depthwise conv.
      nn.Conv2d(C_in, C_in, kernel_size=kernel_size, stride=stride, padding=padding, groups=C_in, bias=False),
      # pointwise conv.
      nn.Conv2d(C_in, C_in, kernel_size=1, padding=0, bias=False),
      nn.BatchNorm2d(C_in, affine=affine),
      nn.ReLU(inplace=False),
      # depthwise conv.
      nn.Conv2d(C_in, C_in, kernel_size=kernel_size, stride=1, padding=padding, groups=C_in, bias=False),
      # pointwise conv.
      nn.Conv2d(C_in, C_out, kernel_size=1, padding=0, bias=False),
      nn.BatchNorm2d(C_out, affine=affine),
    )
  def forward(self, x):
    return self.op(x)

class DilConv(nn.Module):
  def __init__(self, C_in, C_out, kernel_size, stride, padding, dilation, affine=True):
    super(DilConv, self).__init__()
    self.op = nn.Sequential(
      nn.ReLU(inplace=False),
      # depthwise conv.
      nn.Conv2d(C_in, C_in, kernel_size=kernel_size, stride=stride, padding=padding, dilation=dilation, groups=C_in, bias=False),
      # pointwise conv.
      nn.Conv2d(C_in, C_out, kernel_size=1, padding=0, bias=False),
      nn.BatchNorm2d(C_out, affine=affine),
    )
  def forward(self, x):
    return self.op(x)

搜索过程中更新 $\alpha$ 的方法

architect.py

# Architect.step() to update alpha.
class Architect(object):

  def __init__(self, model, args):
    self.network_momentum = args.momentum
    self.network_weight_decay = args.weight_decay
    self.model = model
    # optimizer for α.
    self.optimizer = torch.optim.Adam(self.model.arch_parameters(),
        lr=args.arch_learning_rate, betas=(0.5, 0.999), weight_decay=args.arch_weight_decay)

  # backward of w to compute w' = w - ξ*▽wLtrain(w, α), and construct a model using w'.
  # equal to network_optimizer.step(), but we can't change w to w'.
  def _compute_unrolled_model(self, input, target, eta, network_optimizer):
    loss = self.model._loss(input, target)
    # flatten w to 1D.
    theta = _concat(self.model.parameters()).data
    try:
      moment = _concat(network_optimizer.state[v]['momentum_buffer'] for v in self.model.parameters()).mul_(self.network_momentum)
    except:
      moment = torch.zeros_like(theta)
    dtheta = _concat(torch.autograd.grad(loss, self.model.parameters())).data + self.network_weight_decay*theta
    # return the model with the same α and updated w'.
    unrolled_model = self._construct_model_from_theta(theta.sub(eta, moment+dtheta))
    return unrolled_model

  def step(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer, unrolled):
    self.optimizer.zero_grad()
    if unrolled:
        # bilevel optimization. (another way to compute the gradient of α).
        self._backward_step_unrolled(input_train, target_train, input_valid, target_valid, eta, network_optimizer)
    else:
        # traditional optimization.
        self._backward_step(input_valid, target_valid)
    # update α.
    self.optimizer.step()

  def _backward_step(self, input_valid, target_valid):
    # compute ▽αLval(w, α) directly.
    loss = self.model._loss(input_valid, target_valid)
    loss.backward()

  def _backward_step_unrolled(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer):
    # the network_optimizer contains both w and α.
    unrolled_model = self._compute_unrolled_model(input_train, target_train, eta, network_optimizer)
    # compute Lval.
    unrolled_loss = unrolled_model._loss(input_valid, target_valid)

    unrolled_loss.backward()
    # compute ▽αLval(w', α).
    dalpha = [v.grad for v in unrolled_model.arch_parameters()]
    # compute ▽w'Lval(w', α).
    vector = [v.grad.data for v in unrolled_model.parameters()]
    # compute (▽αLtrain(w+, α) - ▽αLtrain(w-, α)) / (2 * epsilon).
    implicit_grads = self._hessian_vector_product(vector, input_train, target_train)

    # compute ▽αLval(w', α)-eta*(▽αLtrain(w+, α)-▽αLtrain(w-, α))/(2*epsilon).
    for g, ig in zip(dalpha, implicit_grads):
      g.data.sub_(eta, ig.data)

    # update α's gradient.
    for v, g in zip(self.model.arch_parameters(), dalpha):
      if v.grad is None:
        v.grad = Variable(g.data)
      else:
        v.grad.data.copy_(g.data)

    def _construct_model_from_theta(self, theta):
      ...
      return model_new.cuda()

    def _hessian_vector_product(self, vector, input, target, r=1e-2):
      ...
      return "implicit_grads"

连续结构的搜索过程

model_search.py

class MixedOp(nn.Module):

  def __init__(self, C, stride):
    super(MixedOp, self).__init__()
    self._ops = nn.ModuleList()
    for primitive in PRIMITIVES:
      # learnable parameters of BN are banned during searching.
      op = OPS[primitive](C, stride, affine=False)
      if 'pool' in primitive:
        op = nn.Sequential(op, nn.BatchNorm2d(C, affine=False))
      self._ops.append(op)

  def forward(self, x, weights):
    # add each output of operation using weights(softmax of alfa).
    return sum(w * op(x) for w, op in zip(weights, self._ops))

class Cell(nn.Module):

  def __init__(self, steps, multiplier, C_prev_prev, C_prev, C, reduction, reduction_prev):
    super(Cell, self).__init__()
    # Is this a reduction cell?
    self.reduction = reduction

    # first input node, connect the output of C_[k-2].
    if reduction_prev:
      self.preprocess0 = FactorizedReduce(C_prev_prev, C, affine=False)
    else:
      self.preprocess0 = ReLUConvBN(C_prev_prev, C, 1, 1, 0, affine=False)
    # second input node, connect the output of C_[k-1].
    self.preprocess1 = ReLUConvBN(C_prev, C, 1, 1, 0, affine=False)
    # the number of intermediate nodes.
    self._steps = steps
    # the muliplier of cell's output.
    self._multiplier = multiplier

    # the stack of all ops within a cell.
    self._ops = nn.ModuleList()
    self._bns = nn.ModuleList()
    # traverse the intermediate nodes.
    for i in range(self._steps):
      # The inputs of each intermediate node consist of the outputs of all previous nodes
      # including 2 input nodes. (e.g. 3rd intermediate node has 4 ops as its input)
      for j in range(2+i):
        stride = 2 if reduction and j < 2 else 1
        op = MixedOp(C, stride)
        # len: 2 + 3 + 4 + ...
        self._ops.append(op)

  def forward(self, s0, s1, weights):
    # 2 input nodes.
    s0 = self.preprocess0(s0)
    s1 = self.preprocess1(s1)

    # nodes.
    states = [s0, s1]
    # offset indicates the location of intermediate nodes. (e.g. range [offset]->[offset+2] is for 2nd intermediate node)
    offset = 0
    for i in range(self._steps):
      # The output of current intermediate node consists of the sum of op(previous_node).
      # j indicates a certain op source node, h is the current intermediate node.
      s = sum(self._ops[offset+j](h, weights[offset+j]) for j, h in enumerate(states))
      offset += len(states)
      states.append(s)

    # expand the channel of cell's output to multiplier*C.
    return torch.cat(states[-self._multiplier:], dim=1)

class Network(nn.Module):

  def __init__(self, C, num_classes, layers, criterion, steps=4, multiplier=4, stem_multiplier=3):
    super(Network, self).__init__()
    # initial number of channels.
    self._C = C
    self._num_classes = num_classes
    self._layers = layers
    self._criterion = criterion
    self._steps = steps
    self._multiplier = multiplier

    C_curr = stem_multiplier*C
    # stem module before the cell. [C -> stem_multiplier*C]
    self.stem = nn.Sequential(
      nn.Conv2d(3, C_curr, 3, padding=1, bias=False),
      nn.BatchNorm2d(C_curr)
    )
 
    # input nodes for 1st cell: stem, stem; for 2nd cell: stem, 1st cell.
    # C_pre is the number of channels of the previous cell's output.
    # C_curr is the number of channels inside the current cell.
    C_prev_prev, C_prev, C_curr = C_curr, C_curr, C
    self.cells = nn.ModuleList()
    reduction_prev = False
    for i in range(layers):
      # reduction cells appear in the 1/3 and 2/3 of the total depth.
      if i in [layers//3, 2*layers//3]:
        # double the number of channels inside cells. (e.g. C, C, ..., 2*C, 2*C, ..., 4*C, 4*C, ...)
        C_curr *= 2
        reduction = True
      else:
        reduction = False
      cell = Cell(steps, multiplier, C_prev_prev, C_prev, C_curr, reduction, reduction_prev)
      reduction_prev = reduction
      self.cells += [cell]
      C_prev_prev, C_prev = C_prev, multiplier*C_curr

    self.global_pooling = nn.AdaptiveAvgPool2d(1)
    self.classifier = nn.Linear(C_prev, num_classes)

    self._initialize_alphas()

  # copy the model with the same alphas.
  def new(self):
    model_new = Network(self._C, self._num_classes, self._layers, self._criterion).cuda()
    for x, y in zip(model_new.arch_parameters(), self.arch_parameters()):
        x.data.copy_(y.data)
    return model_new

  def forward(self, input):
    s0 = s1 = self.stem(input)
    for i, cell in enumerate(self.cells):
      if cell.reduction:
        weights = F.softmax(self.alphas_reduce, dim=-1)
      else:
        weights = F.softmax(self.alphas_normal, dim=-1)
      # apply the foward pass of cell.
      s0, s1 = s1, cell(s0, s1, weights)
    # [batch_size, C, H, W] -> [batch_size, C, 1, 1]
    out = self.global_pooling(s1)
    # flatten to [batch_size, C].
    logits = self.classifier(out.view(out.size(0),-1))
    return logits

  def _loss(self, input, target):
    logits = self(input)
    return self._criterion(logits, target) 

  def _initialize_alphas(self):
    k = sum(1 for i in range(self._steps) for n in range(2+i))
    num_ops = len(PRIMITIVES)

    # the shape of alphas: [k, num_ops].
    self.alphas_normal = Variable(1e-3*torch.randn(k, num_ops).cuda(), requires_grad=True)
    self.alphas_reduce = Variable(1e-3*torch.randn(k, num_ops).cuda(), requires_grad=True)
    self._arch_parameters = [
      self.alphas_normal,
      self.alphas_reduce,
    ]

  def arch_parameters(self):
    return self._arch_parameters

  # discrete architecure, top-2 strongest ops.
  def genotype(self):

    def _parse(weights):
      # size of gene: number of intermediate nodes x 2.
      gene = []
      n = 2
      start = 0
      for i in range(self._steps):
        end = start + n
        # range[start:end] is the index of an intermediate mode.
        W = weights[start:end].copy()
        # take out the strongest op within each connection, then take out the top-2 op, return its index of source node.
        edges = sorted(range(i + 2), key=lambda x: -max(W[x][k] for k in range(len(W[x])) if k != PRIMITIVES.index('none')))[:2]
        # j indicates the top-2 strongest source nodes.
        for j in edges:
          k_best = None
          for k in range(len(W[j])):
            if k != PRIMITIVES.index('none'):
              if k_best is None or W[j][k] > W[j][k_best]:
                k_best = k
          # k_best is the index of strongest op within the top-2 nodes.
          gene.append((PRIMITIVES[k_best], j))
        start = end
        n += 1
      return gene

    # equal to dim=1, softmax the row vector.
    gene_normal = _parse(F.softmax(self.alphas_normal, dim=-1).data.cpu().numpy())
    gene_reduce = _parse(F.softmax(self.alphas_reduce, dim=-1).data.cpu().numpy())

    concat = range(2+self._steps-self._multiplier, self._steps+2)
    genotype = Genotype(
      normal=gene_normal, normal_concat=concat,
      reduce=gene_reduce, reduce_concat=concat
    )
    return genotype

train_search.py

def main():
  ...
  # starting searching for α.
  for epoch in range(args.epochs):
    ...
    # training.
    train_acc, train_obj = train(train_queue, valid_queue, model, architect, criterion, optimizer, lr)
    logging.info('train_acc %f', train_acc)
    # validation (forward pass only).
    valid_acc, valid_obj = infer(valid_queue, model, criterion)
    logging.info('valid_acc %f', valid_acc)
    # save model.
    utils.save(model, os.path.join(args.save, 'weights.pt'))

def train(train_queue, valid_queue, model, architect, criterion, optimizer, lr):
  objs = utils.AvgrageMeter()
  top1 = utils.AvgrageMeter()
  top5 = utils.AvgrageMeter()

  for step, (input, target) in enumerate(train_queue):
    model.train()
    n = input.size(0)

    input = Variable(input, requires_grad=False).cuda()
    target = Variable(target, requires_grad=False).cuda(async=True)

    # get a random minibatch from the search queue with replacement.
    input_search, target_search = next(iter(valid_queue))
    input_search = Variable(input_search, requires_grad=False).cuda()
    target_search = Variable(target_search, requires_grad=False).cuda(async=True)

    # update α.
    architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)

    optimizer.zero_grad()
    logits = model(input)
    loss = criterion(logits, target)

    loss.backward()
    nn.utils.clip_grad_norm(model.parameters(), args.grad_clip)
    # update w.
    optimizer.step()

    prec1, prec5 = utils.accuracy(logits, target, topk=(1, 5))
    objs.update(loss.data[0], n)
    top1.update(prec1.data[0], n)
    top5.update(prec5.data[0], n)

    if step % args.report_freq == 0:
      logging.info('train %03d %e %f %f', step, objs.avg, top1.avg, top5.avg)

  return top1.avg, objs.avg

def infer(valid_queue, model, criterion):
  ...
  model.eval()

  for step, (input, target) in enumerate(valid_queue):
    ...
    if step % args.report_freq == 0:
      logging.info('valid %03d %e %f %f', step, objs.avg, top1.avg, top5.avg)

  return top1.avg, objs.avg

由genotype生成离散结构

model.py

class Cell(nn.Module):

  def __init__(self, genotype, C_prev_prev, C_prev, C, reduction, reduction_prev):
    super(Cell, self).__init__()
    print(C_prev_prev, C_prev, C)

    if reduction_prev:
      self.preprocess0 = FactorizedReduce(C_prev_prev, C)
    else:
      self.preprocess0 = ReLUConvBN(C_prev_prev, C, 1, 1, 0)
    self.preprocess1 = ReLUConvBN(C_prev, C, 1, 1, 0)
    
    # indices[index_of_intermediate_nodes:...+1]: index of top-2 source nodes.
    if reduction:
      op_names, indices = zip(*genotype.reduce)
      concat = genotype.reduce_concat
    else:
      op_names, indices = zip(*genotype.normal)
      concat = genotype.normal_concat
    self._compile(C, op_names, indices, concat, reduction)

  # size of op_names, indices: 2 x num of intermediate nodes.
  def _compile(self, C, op_names, indices, concat, reduction):
    assert len(op_names) == len(indices)
    self._steps = len(op_names) // 2
    # index of nodes need to be concatened for output.
    self._concat = concat
    self.multiplier = len(concat)

    self._ops = nn.ModuleList()
    for name, index in zip(op_names, indices):
      stride = 2 if reduction and index < 2 else 1
      op = OPS[name](C, stride, True)
      self._ops += [op]
    self._indices = indices

  def forward(self, s0, s1, drop_prob):
    s0 = self.preprocess0(s0)
    s1 = self.preprocess1(s1)

    states = [s0, s1]
    for i in range(self._steps):
      h1 = states[self._indices[2*i]]
      h2 = states[self._indices[2*i+1]]
      op1 = self._ops[2*i]
      op2 = self._ops[2*i+1]
      h1 = op1(h1)
      h2 = op2(h2)
      if self.training and drop_prob > 0.:
        if not isinstance(op1, Identity):
          h1 = drop_path(h1, drop_prob)
        if not isinstance(op2, Identity):
          h2 = drop_path(h2, drop_prob)
      s = h1 + h2
      states += [s]
    return torch.cat([states[i] for i in self._concat], dim=1)

class Network(nn.Module):
  def __init__(self, C, num_classes, layers, auxiliary, genotype):
    ...
  def forward(self, input):
    ...

train.py

def main():
  ...
  for epoch in range(args.epochs):
    ...
    # training.
    train_acc, train_obj = train(train_queue, model, criterion, optimizer)
    logging.info('train_acc %f', train_acc)
    # validation (forward pass only).
    valid_acc, valid_obj = infer(valid_queue, model, criterion)
    logging.info('valid_acc %f', valid_acc)
    # save model.
    utils.save(model, os.path.join(args.save, 'weights.pt'))