生活中的可靠性小案例8：由红绿灯联想到的计时问题以及相对论的钟慢效应

本系列分享一些生活中遇到的可靠性例子，以及从中引发的思考，涉及的知识。

上周末通过佛山12345反馈了一个红绿灯设置不合理的问题。这条马路双向4车道，但人行道绿灯只有10秒。行人刚走几步，绿灯就开始倒计时了，存在巨大交通安全隐患。

我当时反映问题的时候，以为是人为设置的这么短。但昨天我又测了下，发现这个时间又变短了，只有8秒。我想起一个月前我想投诉的时候，这个红绿灯还有13秒。也就是说这个绿灯时间在不断的缩短。

很多红绿灯有根据流量去调整绿信比（在一个周期时间内，有效绿灯时间与周期时间之比）。一开始我怀疑是这个原因。但据我观察，基本没有流量的这边，绿灯反而是时间非常长，而经常过行人的这边，绿灯时间非常短。

因此，我怀疑两个原因：

1.程序写反了，把两个路口的绿信比搞反了，有这种可能。

2.存在计时累积不精确问题。

当然这只是我的猜想，真实原因不清楚。只是从这个事件出发，我联想到了计时问题。

典型的是选择的计时函数不精确导致的累积误差。有很多计时函数，它们的精确度并不是那么精准。

比如C语言的计时函数：time()，可移植性好，性能也很稳定，但精度太低，只能精确到秒，对于一般的事件计时还算够用，而对运算时间的计时就明显不够用了。

又如clock()，可以精确到毫秒，适合一般场合的使用。

而QueryPerformanceFrequency()函数，精度可以到微秒级。

这种由于选择库函数不同导致的计时偏差问题，在编程中应该注意。这点我在软件可靠性系列文章里也有讲过，见《系统性谈谈软件可靠性——第1讲：软件可靠性基础概念》。

从这个案例出发，我又联想到时间偏差问题以及相对论的钟慢效应。

时间偏差是很要命的。比如说导弹，它速度非常快，时间偏差一点，位置就差远了。

又如我们平时用得地图导航，如果定位不精确，那能给你导航到沟里去了。

爱因斯坦的相对论，很重要的一个实际应用就是在提高导航的精度上。下面做个简单的介绍。

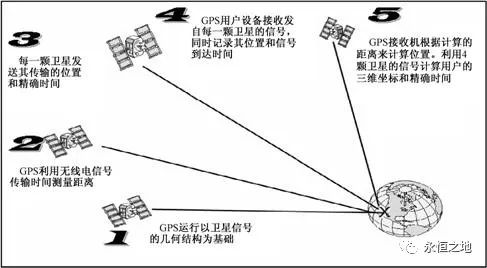
我们都知道导航是靠卫星定位。如图所示，GPS卫星定位的原理如下：

GPS卫星在空中连续发送带有时间和位置信息的无线电信号，供GPS接收机接收。由于传输的距离因素，接收机接收到信号的时刻要比卫星发送信号的时刻延迟，通常称之为时延，因此，可以通过时延来确定距离，根据4颗卫星确定用户的坐标。

​

在以前，想用卫星来测量距离，会产生极其恐怖的误差，今天测在这里，再过10天测量，定位已经跑到110公里外的其他地方。

最核心的原因，就是爱因斯坦狭义相对论中的钟慢效应：速度越快，时间流逝速度就越快。

导航卫星在高速运动，卫星上的时间流逝速度和地面上不一样。因此，如果卫星上和地方上采用同样的时间参数进行计算，就会得出非常离谱的距离差距。

导航的精度有多高，跟你对卫星上带的原子时钟时间的修正精度多高有很大关系（除了这点，还有很多其他因素导致的时间误差，这里不做介绍）。这个时间修正值，就是用相对论计算出来的，公式如下：

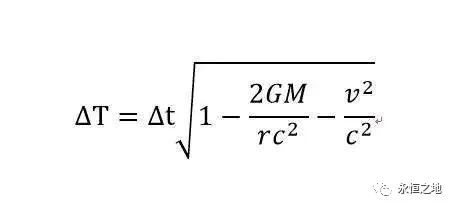
其中：M地球质量，G引力常数，r物体与地球中心距离（注意不是地面距离），v为物体相对地球中心速度，c光速。

根据这个公式计算，导航卫星的时间流逝每天要比地球时间快38微秒，要保证精度，就需要把这38微秒，分到每分每秒去校准，才能保证你任何时打开导航，都是精确的。