超详细！XGBoost原理介绍

本文是袁哲诚本人写的，别算查重了谢谢！XGBoost是现在最流行的三大GBDT模型中，最早的一个，后两个都是在XGBoost的基础上改进的，故本文通过介绍XGBoost来对GBDT模型有一定的认识。

梯度提升树

提升集成算法

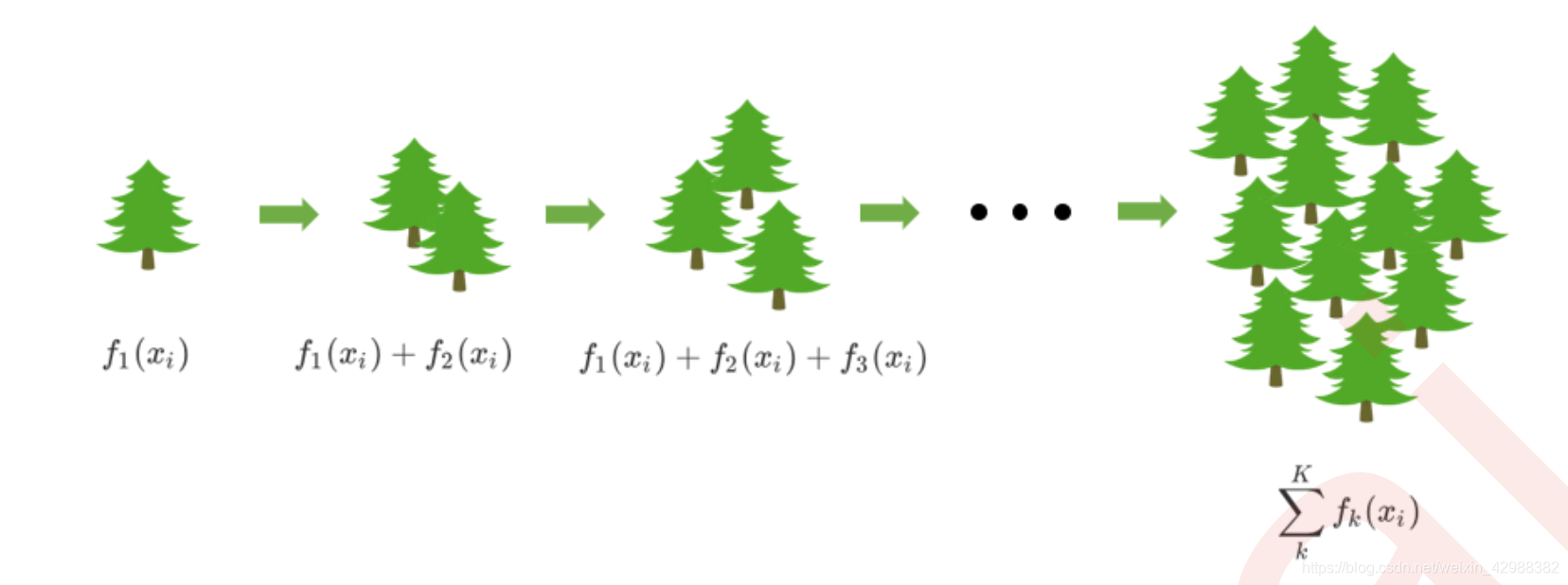
在数据上构建多个弱评估器，汇总所有弱评估器的建模结果，以获取比单个模型更好的回归或分类表现。集成不同弱评估器的方法有很多种，有一次性简历多个平行弱评估器的随机森林，也有逐一构建弱评估器的梯度提升树。梯度提升树可以是回归树也可以是分类树。以下都以梯度提升回归树作为例子。
首先，梯度提升回归树的建模过程大致如下：最开始建立一棵树，然后逐渐迭代，每次迭代过程都增加一棵树，然后逐渐形成众多树模型的强评估器。

对于决策树，每个被放入模型的样本$i$最终都会落到一个叶子节点上。对于普通的回归树，每个叶子节点上的值是这个叶子节点上所有样本的均值。
对于梯度提升回归树而言，每个样本的预测结果，是所有树上的结果的加权求和：
$${\hat{y}}_i=\sum _{k=1}^K{\gamma }_k{h}_k\left(x_i\right)$$
其中$K$是树的总量，$k$代表第$k$棵树，${\gamma }_k$是这棵树的权重，$h_k$表示这棵树上的预测结果(即所有样本的平均)。
XGBoost的优化之一，就是在预测结果上做了优化，它不再是所有样本平均值的加权求和，而是引入了一个预测分数(prediction score)，也称为叶子权重。
$${\hat{y}}_i=\sum _{k=1}^K{f}_k\left(x_i\right)$$
其中$f_k(x_i)$就是预测分数，其他字母和前面的意思是一样的。

参数:n-estimators

通过这一参数来决定一共有多少棵树。
首先，XGB中的树的数量决定了模型的学习能力，树的数量越多，模型的学习能力越强。只要XGB中树的数量足够 了，即便只有很少的数据， 模型也能够学到训练数据100%的信息，所以XGB也是天生过拟合的模型。但在这种情况 下，模型会变得非常不稳定。
第二，XGB中树的数量很少的时候，对模型的影响较大，当树的数量已经很多的时候，对模型的影响比较小，只能有 微弱的变化。当数据本身就处于过拟合的时候，再使用过多的树能达到的效果甚微，反而浪费计算资源。
第三，树的数量提升对模型的影响有极限，最开始，模型的表现会随着XGB的树的数量一起提升，但到达某个点之
后，树的数量越多，模型的效果会逐步下降，这也说明了暴力增加n_estimators不一定有效果。

参数subsample

我们训练模型之前，必然会有一个巨大的数据集。我们都知道树模型是天生过拟合的模型，并且如果数据量太过巨 大，树模型的计算会非常缓慢，因此，我们要对我们的原始数据集进行有放回抽样(bootsrap)。有放回的抽样防止过拟合。
在梯度提升树中，我们每一次迭代都要建立一棵新的树，因此我们每次迭代中，都要有放回抽取一个新的训练样本。 不过，这并不能保证每次建新树后，集成的效果都比之前要好。因此我们规定，在梯度提升树中，每构建一个评估器，都让模型更加集中于数据集中容易被判错的那些样本。(类似于DQN中抽样时加了priority。)
首先我们有一个巨大的数据集，在建第一棵树时，我们对数据进行初次又放回抽样，然后建模。建模完毕后，我们对模型进行一个评估，然后将模型预测错误的样本反馈给我们的数据集，一次迭代就算完成。紧接着，我们要建立第二棵决策树，于是开始进行第二次又放回抽样。但这次有放回抽样，和初次的随机有放回抽样就不同了，在这次的抽样中，我们加大了被第一棵树判断错误的样本的权重。也就是说，被第一棵树判断错误的样本，更有可能被我们抽中。基于这个有权重的训练集来建模，我们新建的决策树就会更加倾向于这些权重更大的，很容易被判错的样本。建模完毕之后，我们又将判错的样本反馈给原始数据集。下一次迭代的时候，被判错的样本的权重会更大，新的模型会更加倾向于很难被判断的这些样本。如此反复迭代。
总体来说这个参数对结果没有太大影响，一般保持默认。

参数：eta($\eta$)

从数据的角度而言，我们让模型更加倾向于努力攻克那些难以判断的样本。但是，并不是说只要我新建了一棵倾向于困难样本的决策树，它就能够帮我把困难样本判断正确了。困难样本被加重权重是因为前面的树没能把它判断正确， 所以对于下一棵树来说，它要判断的测试集的难度，是比之前的树所遇到的数据的难度都要高的，那要把这些样本都判断正确，会越来越难。如果新建的树在判断困难样本这件事上还没有前面的树做得好呢?所以，除了保证模型逐渐倾向于困难样本的方向，我们还必须控制新弱分类器的生成，我们必须保证，每次新添加的树一定得是对这个新数据集预测效果最优的那一棵树。
这里采用了和梯度下降类似的方法：

现在我们希望求解集成算法的最优结果，那我们应该可以使用同样的思路:我们首先找到一个损失函数 ，这个损失函数应该可以通过带入我们的预测结果来衡量我们的梯度提升树在样本的预测效果。然后，我们利用梯度下降来迭代我们的集成算法:
$${\widehat{y_i}}^{(k+1)}={\widehat{y_i}}^{(k)}+f_{k+1}\left(x_i\right)$$
我们让这个过程不断迭代下去，直到找到能够让损失函数最小化的$\hat{y}$。
在XGB中也用一个参数$\eta$来控制迭代速率，使我们的更新方式变成下面这样：
$${\hat{y}}_i^{(k+1)}={\hat{y}}_i^{(k)}+\eta f_{k+1}\left(x_i\right)$$
$\eta$越大，算法收敛越快，到可能无法收敛到最佳；$\eta$越小，可以找到更精确的解，但算法收敛慢。
通常来说$\eta$可以微调以下，大致在[0.01,0.2]之间调整。

梯度提升算法总结

梯度提升算法主要由3部分组成：
1、 一个能够衡量集成算法效果的，能够被最优化的损失函数；
2、一个能够实现预测的弱评估器$f_k(x)$;
3、一种能够让弱评估器集成的手段，比如迭代手段，抽样手段，样本加权等等
XGBoost是在梯度提升树的这三个核心要素上运行，它重新定义了损失函数和弱评估器，并且对提升算法的集成手段进行了改进，实现了运算速度和模型效果的平衡。

XGBoost

XGBoost的目标函数

梯度提升算法中的目标函数是可以选的，针对分类或是回归问题可以选择不同的目标函数。只要它是可微的，并能够代表某种loss即可。
XGB除了传统的损失函数以外，还引入了模型复杂度来衡量算法的运算效率。因此目标函数被写作：传统损失函数+模型复杂度。
$$Obj=\sum _{i=1}^{m}l\left(y_i,{\hat{y}}_i\right)+\sum _{k=1}^K\Omega \left(f_k\right)$$
其中$i$代表数据集中的第$i$个样本，$m$表示导入第$k$棵树的数据总量，K代表目前建立的所有树的总和(n_estimators)，第一项是衡量真实标签与预测值之间的差异的传统损失函数，第二项代表模型的复杂度。使用树模型的某种变换$\Omega$表示。我们在迭代每一棵树的时候，都最小化$Obj$来力求获取最优的$\hat{y}$，因此同时最小化了模型的错误率和模型的复杂度。
还可以从另外一个角度来理解损失函数：通过方差和偏差来理解。通常来说，方差和偏差是此消彼成长的，方差越大，偏差越小。

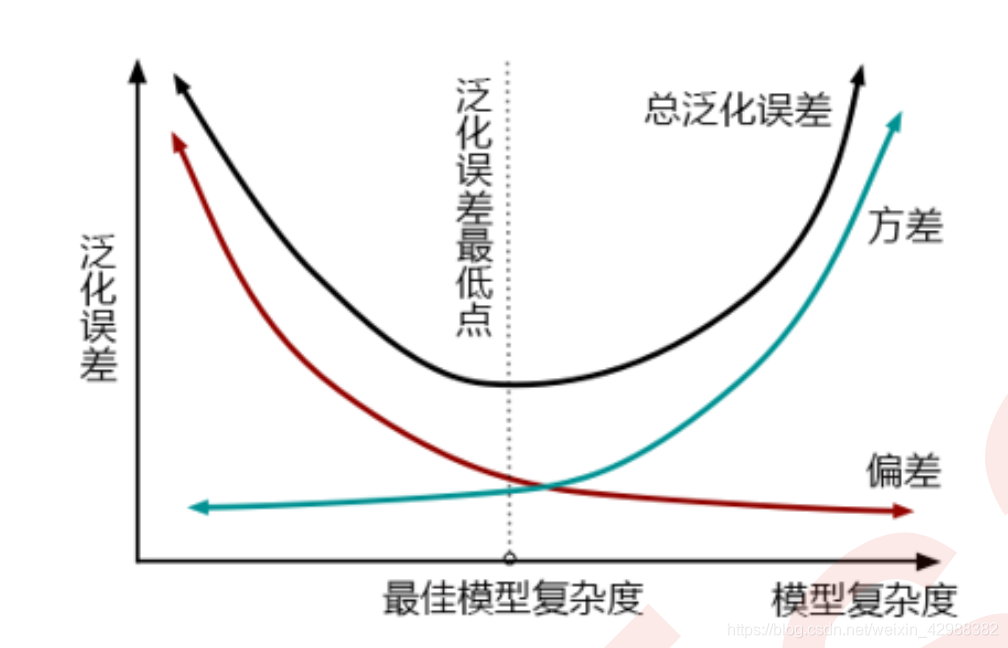
方差可以被简单地解释为模型在不同数据集上表现出来地稳定性，而偏差是模型预测的准确度。那方差-偏差困境就可以对应到我么的$Obj$中了。
$$Obj=\sum _{i=1}^{m}l\left(y_i,{\hat{y}}_i\right)+\sum _{k=1}^K\Omega \left(f_k\right)$$
第一项是衡量我们的偏差，模型越不准确，第一项就会越大。第二项是衡量我们的方差，模型越复杂，模型的学习就会越具体，到不同数据集上的表现就会差异巨大，方差就会越大。所以我们求解的最小值，其实是在求解方差与 偏差的平衡点，以求模型的泛化误差最小，运行速度最快。我们知道树模型和树的集成模型非常容易过拟合，因此大多数树模型最初都会出现在图像的右上方，我们必须通过剪枝来控制模型不要过拟合。现在 XGBoost的损失函数中自带限制方差变大的部分，也就是说XGBoost会比其他的树模型更加聪明，不会轻易落到图像的右上。

求解XGB的目标函数

之前在求解目标函数的时候通常会使用梯度下降或是构造对偶的方式来进行，但在XGB的目标函数中没有需要求解的参数，故不能采用传统的梯度下降。在XGB中，树$f_k$不是数字组成的向量，并且与输入的训练特征矩阵$x$并不直接相关，尽管迭代过程可以与梯度下降类比，但是求解过程完全不同。
在求解XGB的过程中，我们力求将目标函数转化成更简单的，与树的结构直接相关的写法，以此来建立树的结构与模型的效果(包括泛化能力与运行速度)之间的直接联系。也因为这种联系的存在，XGB的目标函数又被称为“结构分数”。
我们的目标函数为：
$$Obj=\sum _{i=1}^{m}l\left(y_i,{\hat{y}}_i\right)+\sum _{k=1}^K\Omega \left(f_k\right)$$
在第$t$次迭代得到的预测结果为：
$$\begin{array}{rl}{\hat{y}}_i^{(t)}=\sum _k^t{f}_k\left(x_i\right)& =\sum _k^{t-1}{f}_k\left(x_i\right)+f_t\left(x_i\right)\\ & ={\hat{y}}_i^{(t-1)}+f_t\left(x_i\right)\end{array}$$
所以目标函数的第一项可以写为：
$$\begin{array}{rl}& \sum _{i=1}^{m}l(y_i,\widehat{y_i})\\ & =\sum _{i=1}^{m}l(y_i^t,{\widehat{y_i}}^{t-1}+f_t(x_i))\end{array}$$
又因为对于某一批数据而言$y_i^t$是一个已知的常数，故可以把$l$函数等效成下面的$F$函数：
$$F({\hat{y}}_i^{t-1}+f_t(x_i))$$
对F函数进行泰勒展开，注意这里的F虽然看上去是一元函数，但其实跟输入的数据是有关的，只不过对于某一批数据而言是一元的，其实是与输入的数据有关的，故l函数本质上是二元函数。所以，这里采用的是偏导而不是全导。这里的展开很多细节需要理解，就不赘述了。
$$\begin{array}{rl}F\left({\hat{y}}_i^{(t-1)}+f_t\left(x_i\right)\right)& \approx F\left({\hat{y}}_i^{(t-1)}\right)+f_t\left(x_i\right)\ast \frac{\partial F\left({\hat{y}}_i^{(t-1)}\right)}{\partial {\hat{y}}_i^{(t-1)}}+\frac{1}{2}{\left(f_t\left(x_i\right)\right)}^2\ast \frac{{\partial }^{2}F\left({\hat{y}}_i^{(t-1)}\right)}{\partial {\left({\hat{y}}_i^{(t-1)}\right)}^2}\\ & \approx l\left(y_i^t,{\hat{y}}_i^{(t-1)}\right)+f_t\left(x_i\right)\ast \frac{\partial l\left(y_i^t,{\hat{y}}_i^{(t-1)}\right)}{\partial {\hat{y}}_i^{(t-1)}}+\frac{1}{2}{\left(f_t\left(x_i\right)\right)}^2\ast \frac{{\partial }^{2}l\left(y_i^t,{\hat{y}}_i^{(t-1)}\right)}{\partial {\left({\hat{y}}_i^{(t-1)}\right)}^2}\\ & \approx l\left(y_i^t,{\hat{y}}_i^{(t-1)}\right)+f_t\left(x_i\right)\ast g_i+\frac{1}{2}{\left(f_t\left(x_i\right)\right)}^2\ast h_i\end{array}$$
现在损失函数的第一项可以化简成下面的形式：
$$\sum _{i=1}^m\left[l\left(y_i^t,{\hat{y}}_i^{(t-1)}\right)+f_t\left(x_i\right)g_i+\frac{1}{2}{\left(f_t\left(x_i\right)\right)}^2{h}_i\right)]$$
现在来讨论一下目前这个形式的损失函数，我们现在是处在第t次迭代，故对于第t次迭代来说，前t-1次迭代所得到的结果都是常数，所以$l(y_i^t,{\hat{y}}_i^{(t-1)})$是常数，$g_i$和$h_i$也是常数，因为我们的泰勒展开是在${\hat{y}}_i^{(t-1)}$处展开的。$g_i$和$h_i$也被称为每个样本的梯度统计量，每个样本都不相同。

再来看目标函数的第二项：,在第t次迭代时
$$\sum _{k=1}^K\Omega (f_k)=\sum _{k=1}^{t-1}\Omega (f_k)+\Omega (f_t)$$
所以前面一项求和相当于也是常数，只有后面那项与当前迭代有关。
这里要提一下，泰勒展开的时候我们做了一个假设，便是需要$f_t(x_i)$是小量，而对于树模型来说，n-estimator一般都几百个的，所以这个假设是成立的，故我们的损失函数最终的形式如下：
$$Obj=\sum _{i=1}^m\left[f_t\left(x_i\right)g_i+\frac{1}{2}{\left(f_t\left(x_i\right)\right)}^2{h}_i\right)]+\Omega \left(f_t\right)$$
这个式子中核心部分是我们需要决定$f_t$的具体形式。

参数化决策树$f_t(x)$

对于XGB来说，每个叶子节点上会有一个预测分数，也被称为叶子权重。所有落在这一叶子节点的样本都有相同的取值，用$f_k(x_i)$或者$w$表示。
当有多棵树的时候，集成模型的回归结果就是所有树的预测分数之和，假设这个集成模型中总共有K棵决策树，则整个模型在样本$i$上的预测结果为：
$$\widehat{y_i}=\sum _{k=1}^K{f}_l(x_i)$$
基于这个理解，我们来考虑每一棵树。对每一棵树，它都有自己独特的结构，这个结构即是指叶子节点的数量，树的 深度，叶子的位置等等所形成的一个可以定义唯一模型的树结构。在这个结构中，我们使用$q(x_i)$表示样本$x_i$所在的叶子节点，并且使用$w_{q(x_i)}$来表示第$i$个样本落到第$t$棵树上的第$q(x_i)$个叶子节点所获得的分数，于是有：
$$f_t(x_i)=w_{q(x_i)}$$
设一棵树上总共包含了$T$个叶子节点，其中每个节点的索引是$j$，则这个叶子节点的样本权重是$w_j$。依据这个，定义模型的复杂度$\Omega (f)$为：
$$\Omega (f)=\gamma T+正则项$$
可以使用L2正则：
$$\begin{array}{l}=\gamma T+\frac{1}{2}\lambda \Vert w{\Vert }^2\\ =\gamma T+\frac{1}{2}\lambda {\sum }_{j=1}^T{w}_j^2\end{array}$$
使用L1正则：
$$\begin{array}{l}=\gamma T+\frac{1}{2}\alpha |w|\\ =\gamma T+\frac{1}{2}\alpha {\sum }_{j=1}^T\left|w_j\right|\end{array}$$
也可以一起使用：
$$=\gamma T+\frac{1}{2}\alpha \sum _{j=1}^T\left|w_j\right|+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
这个结构中有两部分内容，一部分是控制树结构的$\gamma T$ ，另一部分则是我们的正则项。叶子数量$T$可以代表整个树结 构，这是因为在XGBoost中所有的树都是CART树(二叉树)，所以我们可以根据叶子的数量$T$判断出树的深度，而$\gamma$是我们自定的控制叶子数量的参数。
而正则项前面的参数都是用来控制正则化强度的。在XGB中也是如此。当$\lambda$和$\alpha$越大，惩罚越重，正则项所占的比例就越大，在尽全力最小化目标函数的最优化方向下，叶子节点数量就会被压制，模型的复杂度就越来越低，所以对于天生过拟合的XGB来说，正则化可以一定程度上提升模型效果。
在实际应用中，正则化参数往往不是我们调参的最优选择，如果真的希望控制模型复杂度，我们会调整$\gamma$而不是调整这两个正则化参数。对于树模型来说，还是剪枝参数地位更高。

寻找最佳树结构：$w$和$T$

树我们现在使用叶子节点上的预测分数来表达，而树的复杂度是叶子数目加上正则项：
$$f_t\left(x_i\right)=w_{q\left(x_i\right)},\Omega \left(f_t\right)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
假设我们的第$t$棵树的结构已经被确定为$q$，我们可以将树的结构带入我们的损失函数，来继续转换目标函数。转化的目的是：建立树结构（叶子节点的数量）与目标函数之间的关系。XGB默认使用的是L2正则化。
$$\begin{array}{rl}& \sum _{i=1}^m\left[f_t\left(x_i\right)g_i+\frac{1}{2}{\left(f_t\left(x_i\right)\right)}^2{h}_i\right)]+\Omega \left(f_t\right)\\ =& \sum _{i=1}^m\left[w_{q\left(x_i\right)}{g}_i+\frac{1}{2}{w}_{q\left(x_i\right)}^2{h}_i\right]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2\\ =& \sum _{i=1}^m{w}_{q\left(x_i\right)}{g}_i+\left[\sum _{i=1}^m\frac{1}{2}{w}_{q\left(x_i\right)}^2{h}_i\right]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2\end{array}$$
现在还是对样本的个数求和来计算损失函数，现在转化的目标是对叶子节点总数求和来计算损失函数。
假设我们现在有2片叶子和3个样本：

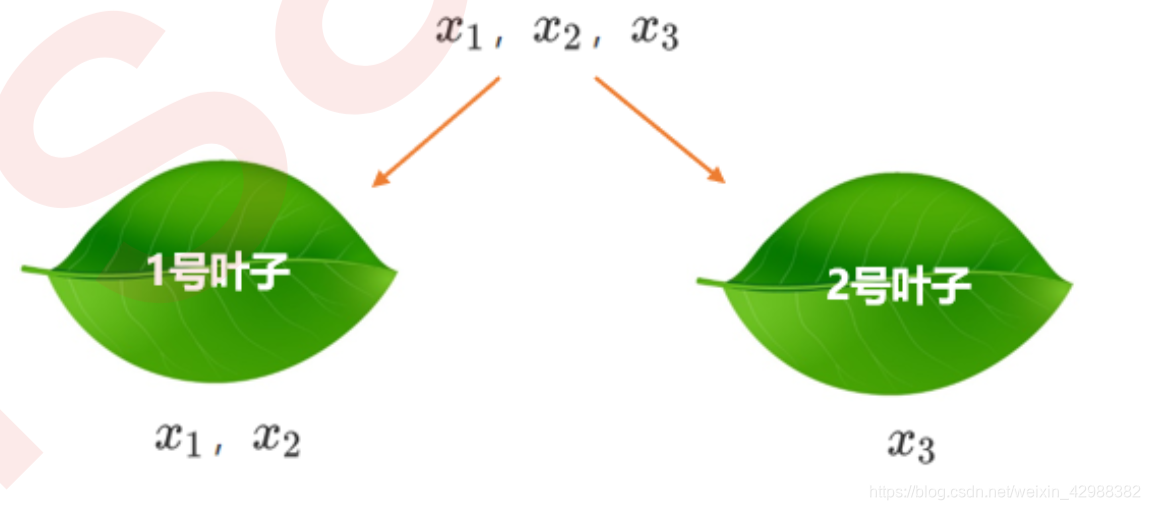
则损失函数的第一项可以通过以下方式来计算：
$$\begin{array}{rl}\sum _{i=1}^m{w}_{q\left(x_i\right)}\ast g_i& =w_{q\left(x_1\right)}\ast g_1+w_{q\left(x_2\right)}\ast g_2+w_{q\left(x_3\right)}\ast g_3\\ & =w_1\left(g_1+g_2\right)+w_2\ast g_3\\ & =\sum _{j=1}^T\left(w_j\sum _{i\in I_j}{g}_i\right)\end{array}$$
这里利用的是每个叶子节点上的$w_j$（$j$是叶子节点的索引下标，我们定义索引为$j$的叶子上所有样本的集合为$I_j$则损失函数可以进一步被转化为：
$$\begin{array}{rl}Obj& =l\sum _{j=1}^T\left(w_j\ast \sum _{i\in I_j}{g}_i\right)+\frac{1}{2}\sum _{j=1}^T\left(w_j^2\ast \sum _{i\in I_j}{h}_i\right)+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2\\ & =\sum _{j=1}^T\left[w_j\sum _{i\in I_j}{g}_i+\frac{1}{2}{w}_j^2\left(\sum _{i\in I_j}{h}_i+\lambda \right)\right]+\gamma T\end{array}$$
我们再定义：
$$G_j=\sum _{i\in I_j}{g}_i,H_j=\sum _{i\in I_j}{h}_i$$
所以损失函数可以变形为如下形式：
$$\begin{array}{r}Ob{j}^{(t)}=\sum _{j=1}^T\left[w_j{G}_j+\frac{1}{2}{w}_j^2\left(H_j+\lambda \right)\right]+\gamma T\\ F^{\ast }\left(w_j\right)=w_j{G}_j+\frac{1}{2}{w}_j^2\left(H_j+\lambda \right)\end{array}$$
其中每个$j$取值下都是一个以$w_j$为自变量的二次函数$F^{\ast }$，我们的目标是追求让$Obj$最小，只要单独的每一个叶子$j$取值下的二次函数都最小，那他们的加和必然也会最小。于是，我们在$F\ast$上对$w_j$求导，让一阶导数等于0以求极值，可以得到：
$$\begin{array}{rl}\frac{\partial F^{\ast }\left(w_j\right)}{\partial w_j}& =G_j+w_j\left(H_j+\lambda \right)\\ 0& =G_j+w_j\left(H_j+\lambda \right)\\ w_j& =-\frac{G_j}{H_j+\lambda }\end{array}$$
我们求得了在给定叶子节点数目$T$的情况下的损失函数最小值，但$T$也是一个要求解的变量，把这一结果带入目标函数可得：
$$\begin{array}{rl}Ob{j}^{(t)}& =\sum _{j=1}^T[-\frac{G_j}{H_j+\lambda }\ast G_j+\frac{1}{2}{\left(-\frac{G_j}{H_j+\lambda }\right)}^2\left(H_j+\lambda \right)\\ & =\sum _{j=1}^T\left[-\frac{G_j^2}{H_j+\lambda }+\frac{1}{2}\ast \frac{G_j^2}{H_j+\lambda }\right]+\gamma T\\ & =-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T\end{array}$$
到了这里，我们的目标函数已经发生了巨大变化。我们的样本量$i$已经被归结到了每个叶子当中去，我们的目标函数是基于每个叶子节点，也就是树的结构来计算。所以，我们的目标函数又叫做“结构分数”(structure score)，分数越低，树整体的结构越好。如此，我们就建立了树的结构(叶子)和模型效果的直接联系。
下面看个具体例子：

对于这棵树的目标函数的计算公式为：
$$Obj=-\left(\frac{g_1^2}{h_1+\lambda }+\frac{g_4^2}{h_4+\lambda }+\frac{{\left(g_2+g_3+g_5\right)}^2}{h_2+h_3+h_5+\lambda }\right)+3\gamma$$
我们会根据损失函数来寻找最佳树结构，从式子中可以看出$\lambda$和$\gamma$都是设定好的超参数，$G_j$和$H_j$都是由损失函数和特定结构下的预测结果${\hat{y}}_i^{t-1}$共同决定的。所以我们最小化目标函数，求解出来的是叶子的数量，所以本质也就是在求解树的结构了。
即每一次迭代，先求解出最佳参数$T$，然后根据树结构求解出$G_j$和$H_j$，然后就可以求解出每个叶子上的权重$w_j$，如此就找到了我们的最佳树结构，完成了一次迭代。
下面就要考虑如何找到最优树结构：

寻找最佳分枝方法：Gain

贪婪算法指的是控制局部最优来达到全局最优的算法，决策树算法本身就是一种使用贪婪算法的方法。XGB作为树的集成模型，自然也想到采用这样的方法来进行计算，所以我们认为，如果每片叶子都是最优，则整体生成的树结构就是最优，如此就可以避免去枚举所有可能的树结构。

决策树中我们是如何进行计算:我们使用基尼系数或信息熵来衡量分枝之后叶子节点的不纯度，分枝前的信息熵与分治后的信息熵之差叫做信息增益，信息增益最大的特征上的分枝就被我们选中，当信息增益低于某个阈值时，就让树停止生长。在XGB中，我们使用的方式是类似的:我们首先使用目标函数来衡量树的结构的优劣，然后让树从深度0开始生长，每进行一次分枝，我们就计算目标函数减少了多少（所以Gain的值是要拿原来的score减去分枝后的score），当目标函数的降低低于我们设定的某个阈值时，就让树停止生长。
举个例子：

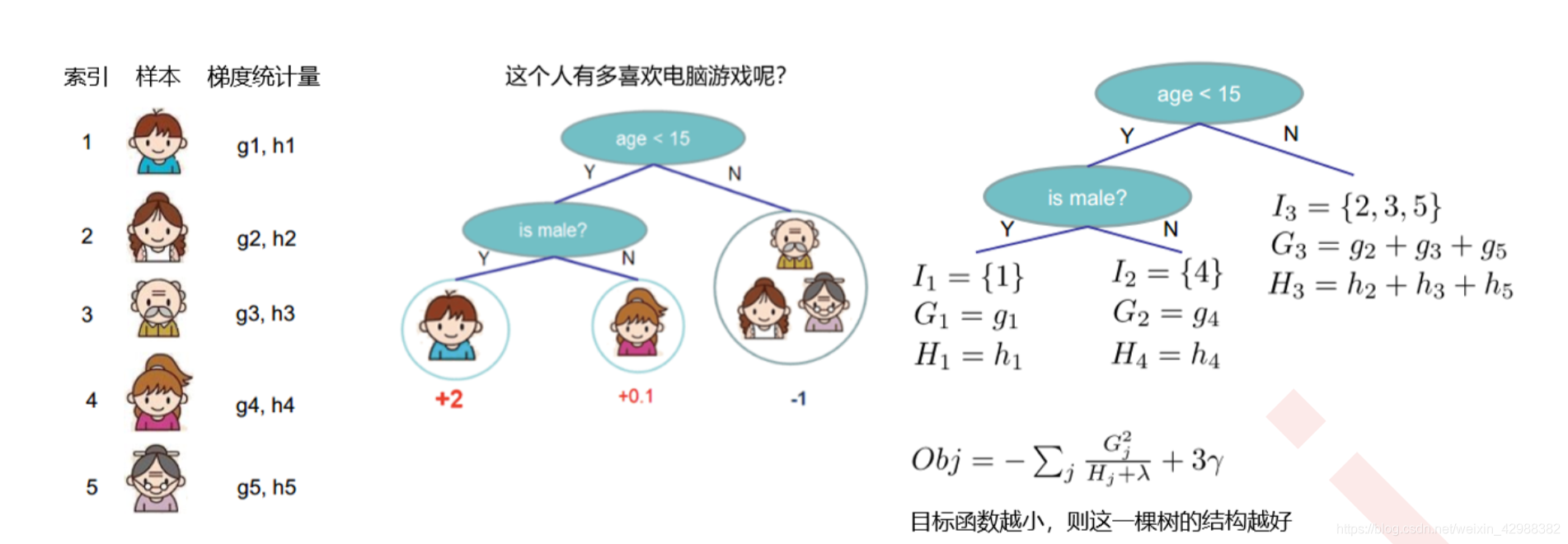
依旧是之前的例子。对于中间节点(is male?)这一个叶子节点而言，我们的$T=1$，这个节点的结构分数为： I = { 1 , 4 } G = g 1 + g 4 H = h 1 + h 4 S c o r e m i d d l e = − 1 2 G 2 H + λ + γ \begin{aligned} I & = \{ 1,4 \} \\ G & = g _ { 1 } + g _ { 4 } \\ H & = h _ { 1 } + h _ { 4 } \\ Score_{middle}&= - \frac { 1 } { 2 } \frac { G ^ { 2 } } { H + \lambda } + \gamma \end{aligned} IGHScoremiddle​​={1,4}=g1​+g4​=h1​+h4​=−21​H+λG2​+γ​
对于弟弟和妹妹节点而言，则有:
$$\begin{array}{rl}Scor{e}_{sister}& =-\frac{1}{2}\frac{g_4^2}{h_4+\lambda }+\gamma \\ Scor{e}_{brother}& =-\frac{1}{2}\frac{g_1^2}{h_1+\lambda }+\gamma \end{array}$$
分枝后的结构分数之差为：
$$\begin{array}{rl}-Gain& =Scor{e}_{sister}+Scor{e}_{brother}-Scor{e}_{middle}\\ & =-\frac{1}{2}\frac{g_4^2}{h_4+\lambda }+\gamma -\frac{1}{2}\frac{g_1^2}{h_1+\lambda }+\gamma -\left(-\frac{1}{2}\frac{G^2}{H+\lambda }+\gamma \right)\\ & =-\frac{1}{2}\frac{g_4^2}{h_4+\lambda }+\gamma -\frac{1}{2}\frac{g_1^2}{h_1+\lambda }+\gamma +\frac{1}{2}\frac{G^2}{H+\lambda }-\gamma \\ & =-\frac{1}{2}\left[\frac{g_4^2}{h_4+\lambda }+\frac{g_1^2}{h_1+\lambda }-\frac{G^2}{H+\lambda }\right]+\gamma \\ & =-\frac{1}{2}\left[\frac{g_4^2}{h_4+\lambda }+\frac{g_1^2}{h_1+\lambda }-\frac{{\left(g_1+g_4\right)}^2}{\left(h_1+h_4\right)+\lambda }\right]+\gamma \end{array}$$
去掉负号后可得Gain的表达式：
$$Gain=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }\right]-\gamma$$
CART树全部是二叉树，因此这个式子是可以推广的。其中$G_L$和$H_L$从左节点(弟弟节点)上计算得出，$G_R$和$H_R$从有节点(妹妹节点)上计算得出，而$(G_L+G_R)$和$(H_L+H_R)$从中间节点上计算得出。对于任意分枝，我们都可以这样来进行计算。在现实中，我们会对所有特征的所有分枝点进行如上计算，然后选出让目标函数下降最快的节点来进行分枝。对每一棵树的每一层，我们都进行这样的计算，比起原始的梯度下降，实践证明这样的求解最佳树结构的方法运算更快，并且在大型数据下也能够表现不错。

重要参数$\gamma$

$\gamma$是我们每增加一片叶子就会就会被减去的惩罚项，增加的越多，Gain就会被惩罚的越重，它可以被用来防止过拟合。
在XGB 中，我们规定，只要结构分数之差$Gain$是大于0的，即只要目标函数还能够继续减小，我们就允许树继续进行分枝。 也就是说，我们对于目标函数减小量的要求是：
$$\begin{array}{r}\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }\right]-\gamma >0\\ \frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{H_L+H_R+\lambda }\right]>\gamma \end{array}$$
如此，我们可以直接通过设定$\gamma$的大小来让XGB中的树停止生长。$\gamma$因此被定义为，在树的叶节点上进行进一步分枝所需的最小目标函数减少量。