傅里叶变换及其应用（一）

前言

记得大学刚开始学傅里叶变换的时候，只觉得这货怎么这么反人类，简简单单地一个函数被它这么一折腾就变得极其繁琐且不知所云。然而，毕业后随着读研究生到后来参加工作逐渐接触到越来越多的实际问题，不禁发出一句感叹，“真香！”。我是从事光电相关行业的，因此接触到大量的傅里叶变换在相关方向上的应用，感叹其带来的便捷。这几篇博文就是想回顾一下傅里叶变换的物理意义，总结一下它的应用。

傅里叶变换的物理意义

先来看一下傅里叶变换的定义：
　　对于任意一个函数$f(x)$，它的傅里叶变换定义为：
　　　　$F(f_x)={\int }_{-\infty }^{+\infty }f(x)e^{-i2\pi f_x}dx$
这个公式看起来就很复杂，我们先不管它，直接来看看这个变换干了什么事。我们使用Matlab作为仿真的工具，计算函数$f(x)=x^2$的傅里叶变换，如下所示：

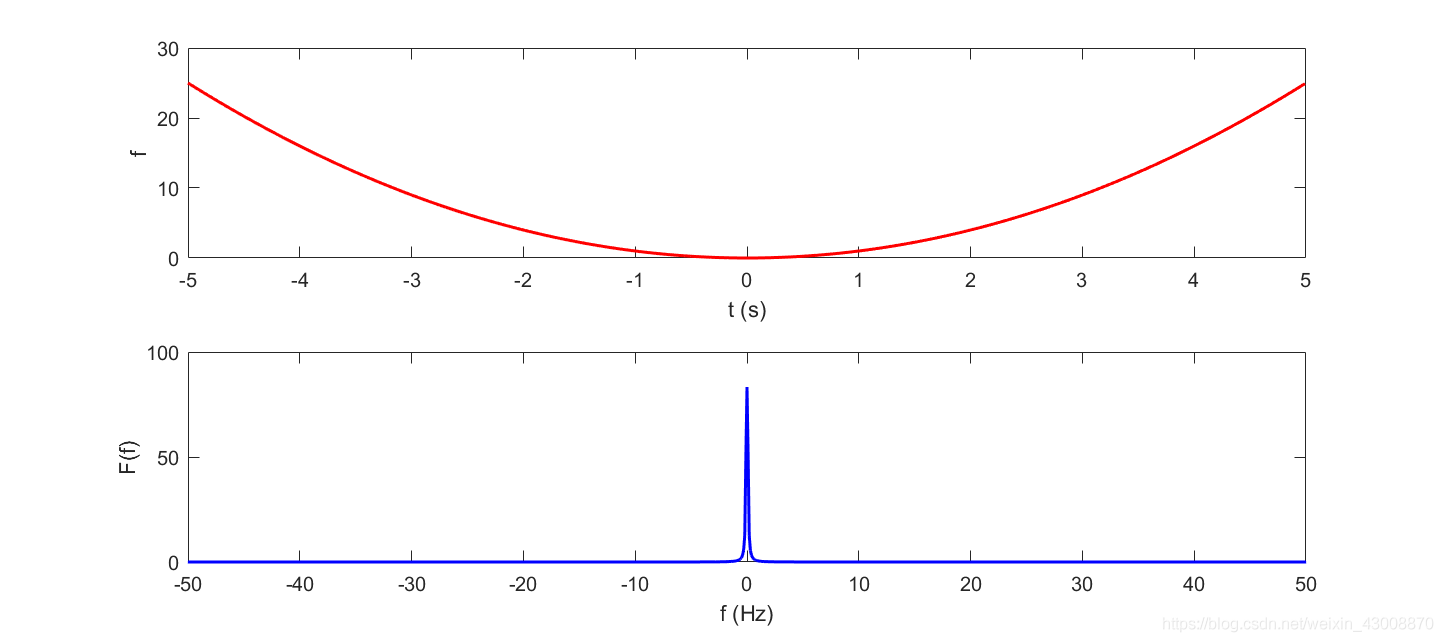
好好地一条抛物线变成了一个尖峰，好像也看不出什么意义。
　　接下来，我们用一个具有周期性的函数做变换来看一下它的意义。我们定义函数$f(t)=sin(\frac{2\pi }{T}t)$，其中$T=\frac{1}{5}$是函数的变化周期，然后再来看它的傅里叶变换：

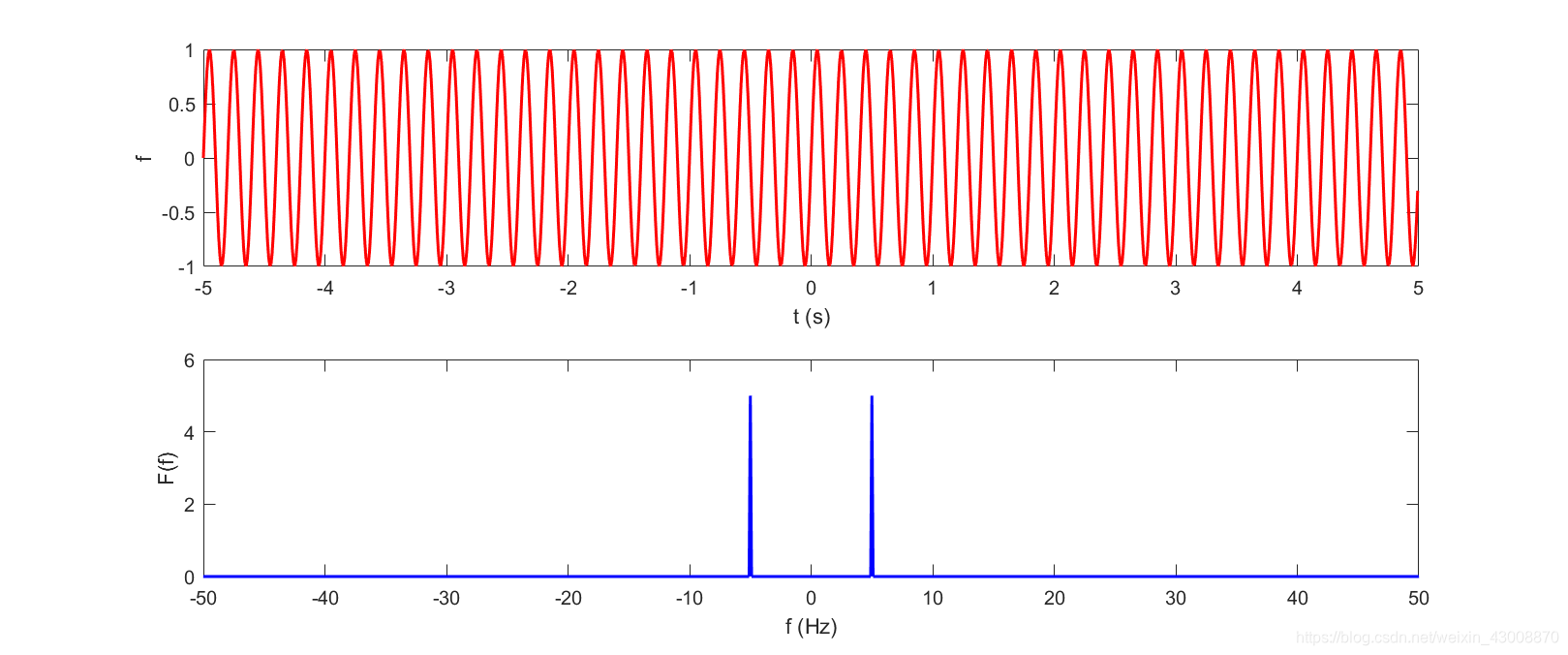
这回好像有点意思了，这个周期函数的傅里叶变换结果是两个尖峰。我们看曲线的右半部分也就是频率大于0的区域，这个区域上有一个尖峰，尖峰的位置正好等于$\frac{1}{T}$，也就是函数$f(t)$的变化频率。
　　接下来，我们再来看另一个有多个变化周期的函数：
　　　　$f(t)=3\ast sin(\frac{2\pi }{T_1}t)+1\ast sin(\frac{2\pi }{T_2}t)+4\ast sin(\frac{2\pi }{T_3}t)$。
这个函数里包含了3个变化周期，分别令$T_1=\frac{1}{5},T_2=\frac{1}{8},T_3=\frac{1}{10}$，并且这三个周期的变化强度之比为$3:1:4$，这个时候，我们再来看傅里叶变换的结果：

这个时候我们发现，傅里叶变换后的函数好像比原来的函数简洁了很多。原来的函数由于各种频率混杂，变化规律变得很复杂，但是经过傅里叶变换后就只有三个尖峰了（当然，我们仍然只看曲线的右半部分）。再仔细看的话，我们发现这三个尖峰的位置正好等于原函数里包含的三个周期函数的频率，而峰的高度之比也正好等于三个周期函数的强度之比。
　　到这里，傅里叶变换的物理意义就很明显了，它的作用就是提取出原函数中的震荡频率和强度。如果原来函数中有很多中震荡频率，傅里叶变换以后得到的就是原函数的震荡频率谱。
　　换而言之，任何一个函数，都有一个对应的震荡频谱，如果它是一条直线，那么它只包含一个频率为0的震荡分量；如果它是一个频率固定的正弦曲线，那么它只包含一个该频率下的震荡分量；如果它是一个任意变化的曲线，它就包含多个震荡分量，例如我们一开始用的抛物曲线。也就是说，任意一条函数曲线，我们都可以把它看成是由很多个不同强度、不同频率和相位的正弦曲线叠加而成。而这些正弦曲线的频率和强度分布就是我们看到的傅里叶变换曲线。
　　如果回到最初的傅里叶变换的定义，我们会发现，原函数经过傅里叶变换以后应该是一个复函数。这个复函数既包含了所有频率分量的强度信息，也包含了它们的相位信息，而大多数情况下，我们只关心这些频率分量的强度信息，因此，通常对这个复函数取绝对值，也就是我们上面画的曲线了。
　　明白了傅里叶变换的数学意义后，我们还有一个疑问，就是为什么我们这么关心一个函数的频率谱呢？在实际应用中，一个函数可以看成是某个系统的输出信号和输入信号之间的映射，这个系统可能是一块电路板、一块镜片或者一块物质等等。而自然界中很多情况下，这个系统是线性的，也就是它不改变输入信号的频率只改变不同频率的强度，例如，地震时，震源处的振动频率传播到地表后仍然是这个频率，只是有的频率衰减得快，有的频率衰减的慢而已。而对不同频率的衰减程度就是这个系统的本征属性，也就是它的傅里叶变换谱了。所以，从某种程度上说，傅里叶变换其实更能反映出一个函数或者说一个系统的本质。下一节，我们结合一些实际的系统来聊聊傅里叶变换的应用。

附：Matlab代码

下面附上以上示例中用到的Matlab代码：

clc;clear all;close all;

tm=10;%时间长度
N=2^10;%采样点数
dt=tm/N;%最小时间间隔
t=(-N/2:N/2-1)*dt;%时间序列
freq1=5;%三个频率分量
freq2=8;
freq3=10;
f=3*sin(2*pi*freq1*t)+1*sin(2*pi*freq2*t)+4*sin(2*pi*freq3*t);%原函数

Ft=ft(f,dt);%傅里叶变换
df=(-N/2:N/2-1)/tm;%频率序列

figure,
subplot(211),
plot(t,f,'linewidth',1.5,'color','red');
xlabel('t (s)');
ylabel('f');
subplot(212),
plot(df,abs(Ft),'linewidth',1.5,'color','blue');
set(gca,'xLim',[-50,50]');
xlabel('f (Hz)');
ylabel('F(f)');

function G=ft(g,delta)
G=fftshift(fft(fftshift(g)))*delta;