逻辑回归的常见问题

逻辑回归概括

逻辑回归假设数据服从伯努利分布，采用极大似然估计的思想，运用梯度下降法来求解参数，达到将数据二分类的目的。

逻辑回归的基本假设

逻辑回归的第一个基本假设是假设数据服从伯努利分布（0-1分布）
逻辑回归的第二个假设是假设样本为正的概率（假设函数） $h(x)=sigmoid(w^{T}X)$

逻辑回归的损失函数

我们采用似然函数作为模型更新的loss，最大化似然函数

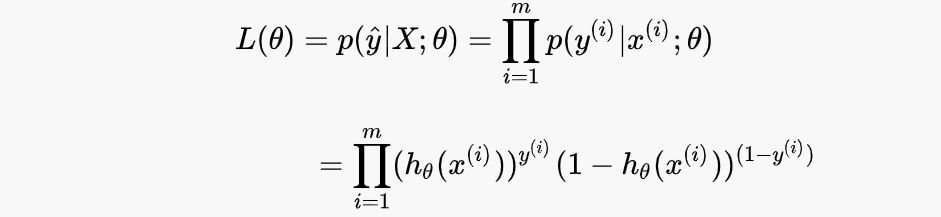
这个损失函数很难求导，于是我们将其取log，变成对数似然函数并转化为

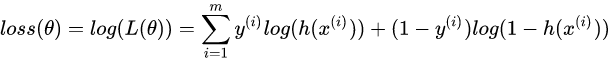
交叉熵损失函数的原理

单个样本的交叉熵损失函数：

$L=-[y\log \hat{y}+(1-y)\log (1-\hat{y})]$

为什么它能表征真实样本标签和预测概率之间的差值？也就是交叉熵损失函数的数学原理。

因为Sigmoid 函数的输出表征了当前样本标签为 1 的概率，因此也可以表示成：$\hat{y}=P(y=1|x)$，

对应的，当前样本标签为 0 的概率就可以表达成：$1-\hat{y}=P(y=0|x)$

把上面两种情况整合到一起：
$P(y|x)=P(y=1|x{)}^y\ast P(y=0|x{)}^{(1-y)}$

即：

$P(y|x)={\hat{y}}^y\cdot (1-\hat{y}{)}^{1-y}$

我们希望的是概率 P(y|x) 越大越好。极大似然估计，是在给定当前样本结果的情况下，反推最有可能导致这样结果的参数值，要求的是似然函数最大，或者说损失函数最小时，对应的参数。

首先，我们对 P(y|x) 引入 log 函数，因为 log 运算并不会影响函数本身的单调性。则有：

$\log P(y|x)=\log \left({\hat{y}}^y\cdot (1-\hat{y}{)}^{1-y}\right)=y\log \hat{y}$