验证牛顿公式的局部收敛性，并找到对于牛顿公式不收敛（发散）的函数，比较二分法与牛顿公式的收敛速度

文末有代码，大家可以自己跑一下，体会一下牛顿法的运算过程

二、实验目的：

a.验证牛顿公式的局部收敛性；
b.比较二分法与牛顿公式的收敛速度；
c.验证求解结果的正确性；

三、实验内容

a.在验证牛顿公式的时候，首先让用户输入一个初始的近似根x0，再输入迭代次数的上限N，N的目的是防止函数f(x)在x0处使用牛顿法时不收敛而造成程序的死循环。最后提示用户输入迭代结果的精度e，当|xk+1 - xk| < e时，程序执行结束，输出迭代结果和迭代次数。在程序代码里定义一个整形变量k，用于记录迭代的次数。
b.在上面的基础上，再编写一个用二分法求根的函数，从而实现二分法与牛顿法收敛速度的比较。执行二分法的代码时，用户需要输入二分的区间端点a，b。二分结果的精度可以使用牛顿法的精度e，当|b - a| < e时，函数执行结束，并输出二分结果和二分次数。
c.选取的验证函数应该有实根，且在程序执行之前我们能够通过其它方法得到被验证函数的所有实根。最后比较程序计算出来的根和预先已知的根是否相同来验证求解结果的正确性。
d.因为牛顿法是局部收敛的，所以一定能够找到使牛顿法不收敛的点。我采用的是构造函数的方法来寻找不收敛点，不收敛有两种情况，如下图所示：

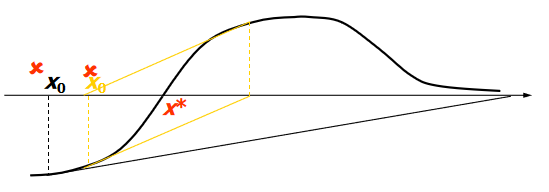
下面介绍第一种情况的构造。

这种构造方法的核心思想是在点（b，f(b)）处的切线的横截距等于a，点（a,f(a)）处切线的横截距等于b。因为f(x) = 0必须有实根，所以假设f( c ) = 0,c除了a，b外，可以取任意实数，而a，b是可以任取的。
第二种情况的构造。

这种不收敛情况下的构造，我们首先需要画出一个某一区间上牛顿法不收敛的函数图像（满足这个要求的图像并不难画，关键是画的越简单越好）。构造函数的核心思想是对函数f（x）进行分段，按照牛顿法的要求，f（x）必须是连续且一阶可导，我们把这两点作为条件，可以得到两个方程。先设出f（x）其中一段函数的表达式，在设表达式的时候，基本上我们学过的初等函数就能满足要求，因为我们并不需要所设的表达式与画出的曲线图完全吻合，只要变化趋势一致即可。
四、程序关键语句描述

double f(float x) {
	double result;
	result = (5.0 / 6.0) * pow(x, 4) - 4 * pow(x, 3) + (23.0 / 6.0) * pow(x, 2) + 3 * pow(x, 1) - (17.0 / 3.0);	//不收敛点是1和2,根为-1和3,2
		return result;
}

上述代码用来求函数f(x)的函数值，我构造出来的这个函数在x = 1和x=2处对于牛顿法不收敛。

double f_d(float x){	
	double result;
		result = (10.0 / 3.0) * pow(x, 3) - 12 * pow(x, 2) + (23.0 / 3) * pow(x, 1) + 3;
		return result;
}

上述代码用来求函数f（x）的一阶导数值。
因二分法和牛顿法的代码都比较简单这里不做赘述，牛顿法的公式为

五、实验结果
待检验函数f(x)的表达式是f(x) = (5/6)*x4-4x3+(23/6)x2+3x-(10/3)，它有两个实根，分别为x1 = -1，x2 = 3.23483652635，函数图像如下图所示。

此函数对于牛顿法不收敛的点为1和2.
对于初始近似根x=3的牛顿法和二分区间[2,4]的二分法，看他们的收敛速度的情况，如下图所示，对于同样的精度要求，二分法需要计算21次，而牛顿法只需计算5次。

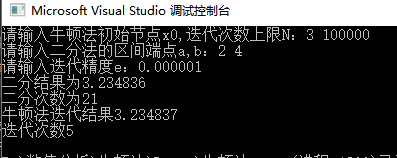
验证对于牛顿法不收敛的点


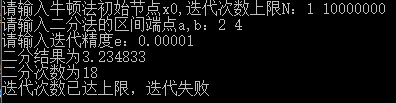
六、实验体会
通过本次实验，加深了对牛顿法的理解，同时也领悟到牛顿法思想的简洁性和可操作性。牛顿法的收敛性非常强，对于绝大多数函数都收敛，只有极少部分函数在少数点不收敛，因此牛顿法具有很强的实用性。当我用分段构造法构造出来的函数进行验证的时候，发现程序执行过程中出现来了奇异点。经过分析之后，发现是由于计算机的计算精度不够造成的。这也提醒我们，在实际应用中，不能只是依靠理论推导，还应该对实际环境进行充分的调研，理论结合实践，才能得到最优的结果。
最后上代码

// 牛顿法.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//
 
//#include "pch.h"
#include "stdio.h"
#include"math.h"
//计算法（x）的值
double f(float x) {
	double result;
	//result = (pow(x, 3) - 2 * pow(x,2) - pow(x,1) + 2) * (5.0 / 6.0 * pow(x,1) - 7.0 / 3.0) - (x + 1);	//不收敛点是1和2,根为-1和3.2
	result = (5.0 / 6.0) * pow(x, 4) - 4 * pow(x, 3) + (23.0 / 6.0) * pow(x, 2) + 3 * pow(x, 1) - (17.0 / 3.0);
	//if (x > 0)
	//	result = exp(-x) + 1;
	//else
	//	result = -pow(x, 2) - pow(x, 1) + 2;
	return result;
}
//f（x）的一阶导数
double f_d(float x){	
	double result;
	//result = (3 * pow(x,2) - 4 * pow(x,1) - 1) * (5.0 / 6.0 * x -7.0 / 3.0) + (5.0 / 6.0) * (pow(x, 3) - 2 * pow(x, 2) - pow(x, 1) + 2) - 1;
	result = (10.0 / 3.0) * pow(x, 3) - 12 * pow(x, 2) + (23.0 / 3) * pow(x, 1) + 3;
	//if (x > 0)
	//	result = -exp(-x);
	//else
	//	result = -2 * pow(x, 1) - 1;
	return result;
}
int main()
{
	float x0,x1, e;
	int N,k = 1;	//k用来记录迭代的次数
	printf("请输入牛顿法初始节点x0,迭代次数上限N：");
	scanf("%f%d", &x0, &N);
	float a, b;
	printf("请输入二分法的区间端点a,b：");
	scanf("%f%f",&a,&b);
	printf("请输入迭代精度e：");
	scanf("%f", &e);
	if (f(a) * f(b) >= 0) {	//根在区间端点的情况也不可以。
		printf("区间端点有误，此开区间无根或有多个根\n");
		return 0;
	}
	//二分法的计算
	while (1) {
		//判断是否恰好为根
		if (f(a) * f((a + b) / 2.0) == 0) {
			printf("二分结果为%f\n二分次数为%d\n", (a + b) / 2.0, k);
			break;
		}
		if (f(a) * f((a + b) / 2.0) < 0)
			b = (a + b) / 2.0;
		else
			a = (a + b) / 2.0;
		//如果满足精度要求，则输出二分结果
		if ((fabs(a - b) < e)) {
			printf("二分结果为%f\n二分次数为%d\n", a, k);
			break;
		}
		k++;
	}
	//牛顿法的计算
	k = 1;
	while (1) {
		if (f_d(x0) == 0) {
			printf("此点为奇异点，迭代失败\n");
			printf("现在的迭代次数为%d", k);
				break;
		}
		x1 = x0 - f(x0) / f_d(x0);
		
		if (fabs(x1 - x0) < e) {
			printf("牛顿法迭代结果%f\n迭代次数%d\n", x1,k);
			break;
		}
		if (k == N) {
			printf("迭代次数已达上限，迭代失败\n");
			break;
		}
		k++;
		x0 = x1;
	}

}