数据结构--图--的小总结

图

2019年7月22日
22:30

（1）图的简单概念

• 顶点（vertex）：图中的数据元素，V是顶点的一个有穷非空集合

• VR：顶点关系的集合。

• 弧（Arc）：若<v,w>属于VR， 则<v,w>表示从v到w的一条弧，弧是有向的，边（Edge）是无向

• 有向图（Digraph）：弧<v,w>为有序对

• 无向图（Undigraph）：边(v,w)为无序对

• 完全图（Completed graph）：有0.5 * n * （n-1）条边，n为顶点个数

• 有向完全图：有n * （n-1）条弧，n为顶点个数

• 稀疏图（Sparse graph）：有很少边或弧的图

• 稠密图（Dense graph）：有很多边或弧的图

• 权（Weight）：与图有关的边或弧相关的数，这些全部可以表示从一个顶点到另一个顶点的距离或者耗费

• 网（Network）：带权的图

• 邻接点（adjacent）：对于无向图G=（V， {E}），如果边（v,v1）属于E，则称顶点v和v1为邻接点，边（v,v1）依附于顶点v,v1，或者说边（v,v1）和顶点相关联，有e（Edge） = 0.5 * 度（Degree）

• 入度（Indegree），出度（Outdegree），有e（Arc）= 0.5 * 【indegree（vi）+ outdegree（vi）】,注释：vi表示第i条边。

• 路径的长度：路径上的边或者弧的数目。

• 回路/环（Cycle）：第一个顶点和最后一个顶点相同的路径

• 简单路径：路径上的顶点不重复出现的路径

• 简单回路/简单环：除了第一个和最后一个顶点之外，其余顶点不重复的回路。

• 连通：在无向图G中，如果从顶点v到顶点v1有路径，则称v和v1是连通的。

• 连通图（Connected graph）：对于图中的任意两个顶点vi，vj属于V，vi和vj都是连通的，则称G是连通图。

• 连通分量（Connected component）：是无向图中的极大连通子图。如1，2，3都是G3的连通分量。

• 强连通图：有向图的连通图。

• 强连通分量：有向图的连通分量。

• 生成树：一个连通图（无向）的极小连通子图（无环）。
  极小连通子图：有全部的n个顶点，有n-1条边的连通子图。

（2）图的存储结构

• 顺序映像结构：数组
• 链式映像结构：链表

1，邻接矩阵：

• 时间复杂度O（n^{2+e*n）其中n}2为初始化，e*n为建立变之间的关系。
• 无向图：顶点vi的度为第i行（列）的元素之和。
• 有向图：顶点vi的度为第i行（出度数）和第i列（入度数）元素之和。

2，邻接表：

无向图：

有向图：

3，十字链表：是有向图的另一种链式存储结构

4，邻接多重表：是无向图的另一种链式存储结构

（3）图的遍历

1，深度优先遍历（Depch_First Search）:

• 概念：从图概中的某个顶点v出发，访问此点，然后依次从v未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到；若此图还有顶点未被访问，则选图中另一个未曾被访问的顶点作为起点，重复上述过程。
• 结果：v1 v2 v4 v8 v5 v3 v6 v7

2，广度优先遍历（Breadth_First Search）：

• 概念：访问图中某顶点v，之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。
• 结果：v1 v2 v3 v4 v5 v6 v7 v8

3，生成树：连通图的极小连通子图（无环）

一个生成树为：

4，最小生成树：（prim和kruskal算法）

• MST性质：假设N = （V， {E}）是一个连通网，U是顶点集合V的一个非空子集。若（u，v）是一条具有最小权值（代价）的变，其中u∈U，v∈V-U，则必存在一颗包含边（u，v）的最小生成树。

• prim算法：时间复杂度O（n^2），适合边稠密的图。

  
  

• kruscal算法：时间复杂度O（e*log e），适合边稀疏的图

  • 概念：假设连通网N = （V，{E}）。则令最小生成树的初始状态为只有n个顶点而无边的非连通图T = （V，{}），图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边的顶点落在不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。
  • 图解：

  
  

顶点活动网（Activity On Vertex Network）AOV网（不出现环）

• 概念：顶点表示活动，边表示活动的先后关系的有向无环图。

边表示活动网（Activity On Edge）AOE网（不出现环）

• 概念：顶点表示活动，边表示活动的先后关系，权表示活动持续的时间。

拓扑排序

• 概念：由某个集合上的偏序得到该集合上的全序的操作称为拓扑排序。
  即：在AOV网中，若不存在回路，则所有活动可以排成一个线性序列，使得每个活动的前驱活动都排在该活动之前，我们把此序列称作拓扑序列（Topological order），由AOV网构造托剖序列的过程称为拓扑排序。

• 构造方法：
  （1）在有向图中选一个没有前驱的顶点且输出之。
  （2）从图中删除该顶点和所有以它为尾的弧。
  （3）重复直到所有的点均已输出。

• 示例：

第一次构造：

输出为v1。
最后依次输出为：v1，v2，v3，v4，v5，v6

最短路径

• Dijkstra算法：

  • 基本原理：
    假设arcs[i][j]为顶点i和j边上的权值，即为一个邻接矩阵。
    （1）选定一个顶点vi，vi到终点的距离设为D[i]。
    （2）选中一个终点vj ∈ min{ D[j]， j ∈ 剩余顶点 }，使得vi -> vj最小。
    （3）在剩余的点中选择一个顶点vk，进行如下计算：
    若 D[j] + arcs[j][k] < D[i] //表示vi -> vk的距离大于vi -> vj -> vk的距离
    做如下更新:
    D[k] = D[j] + arcs[j][k]
    重复（2）（3）步骤。

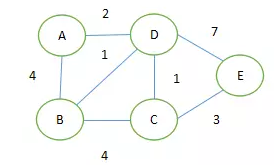
  • 例图：

D[D] = 2
D[B] = 4
D[C] = ∞
D[E] = ∞

第一次执行：
选择D，
因为

D[D] + arcs[D][B] < arcs[A][B]

故更新

D[B] = D[D] + arcs[D][B]

依次执行就可以获得到各个终点的最短路径。