【指数编制系列六】景气指数编制方法

  景气是经济景气的简称，指经济总体的运行发展态势和活跃程度，是用来分析经济活跃程度的经济概念。经济活动发展具有周期性扩张的特征，因而常用景气波动、景气循环等术语来表达经济周期波动的特点。
  经济景气周期波动理论是研究产业景气周期波动的理论基础，因此研究产业景气周期波动必须了解经济景气周期波动分析理论与实践的发展。经济周期波动的研究最早可回溯到19世纪50年代马克思、恩格斯揭示资本主义经济危机和经济周期的根源。马克思认为经济危机的发生具有周期性，从一次危及到下一次危机要依次经历萧条、复苏、高涨、衰退四个阶段，并提出用数学方法研究经济周期波动。随着统计、计量及运算手段的逐渐发展和统计数据的大量积累，定量地分析和预测经济周期波动具有可操作性并深入发展。
  我国景气指数研究开始于20世纪80年代后期，主要是在引进西方经济发展理论和经济波动周期理论基础上，分析我国经济波动成因，并借鉴西方景气指数编制方法，研究适合我国国情的景气监测系统。1987年，吉林大学董文泉课题组首次编制出我国宏观经济周期波动的CI和DI。1988年，国家信息中心首次发布了我国经济预警信号系统。进入90年代后，我国经济景气监测研究日趋完善和深入，其中影响较大的是吉林大学董文泉和东北财经大学高铁梅两位学者。董文泉等（1995）运用数学模型实证分析S-W景气指数在我国经济波动预测分析中的有效性；1998年，由董文泉、高铁梅等合著的《经济周期波动的分析与预测方法》一书是系统阐述景气波动分析理论最具代表性的著作，书中的经济周期波动分析与预测技术在实际应用中获得了国际信息中心的认可。直到21世纪初，经济景气波动分析理论和监测技术才开始被应用在行业景气波动分析中，常用的景气指数编制方法有合成指数编制方法、扩散指数编制方法、主成分分析法等。

景气指数的主要方法

  目前国内外景气指数编制方法有扩散指数DI方法、合成指数CI方法、主成分分析方法和S-W型景气指数法。
1. 扩散法
  按照经济周期理论，经济运行可以划分为扩张和收缩两种状态。经济扩张时，大部分经济指标持续上升。当经济运行中少数指标开始改变方向，随着时间推移下降的指标数量增多，保持上升的指标与转为下降的指标均等时，经济景气由扩张转向收缩（即景气的高峰）。反之，经济收缩阶段下降指标占据上风，随着景气前景明朗，少数指标转向上升并且数量逐渐增多，当仍在下降的指标与上升的指标均等时，经济景气由收缩转向扩张（即景气的低谷）。扩散指数的计算方法主要分为四步。
  第一步：首先计算各指标各年月距环比发展速度，然后消除季节变动和不规则变动影响，从而使各指标序列比较稳定地反映循环波动。
  第二步：将每个指标各年月距环比发展速度与其比较基期的发展速度相比，若当月值大，则为扩张，此时I=1；若当月值小，则为收缩，此时I=0；若两者基本相等，则I=0.5。
  第三步：将这些指标升降应得的数值相加，即得出“扩张的指标数”，即在t时刻扩张的变量个数。
  第四步：以扩张指标数除以全部指标数，乘以100%，即得扩散指数（DI）。
  由此可见，50%是扩散指数DI的临界点，当DI>50%时，半数以上经济指标上升，经济处于景气状态，反之，当DI<50%时，半数以上经济指标下降，经济处于不景气状态。因此，扩散指标可以用来判断经济景气运行所处的状态，但其数值的大小（百分比水平）却不能表示经济周期波动的振幅。
2. 合成法
  合成指数是从各种宏观经济活动中选取对景气波动敏感的指标，合成各指标变化率的方法监测经济景气变动的强弱。CI不仅可以预测经济周期波动的转折点，还能反映其波动变化的强弱程度，弥补扩散指数的不足之处。目前合成指数编制方法有三种，美国商务部、日本经济企划厅、经济合作与发展组织三家机构使用不同的合成指数编制方法。其中美国商务部与日本经济企划厅的计算方法思想上是一致的，但方法上略有不同，经济合作与发展组织基于“增长循环”，用阶段平均法分离趋势要素后，确定各成员国基准日期进而编制合成景气指数。美国商务部的合成指数编制方法的构建过程有五个步骤：
  第一步、计算指标的对称变化率并标准化
  令$Y_{ij}(t)$为第j指标组（j=1，2，3分别代表先行、一致、滞后指标组）的第i个指标$（i=1，2，\dots ，k_j）$，对$Y_{ij}(t)$求对称变化率$C_{ij}(t)$：
$$C_{ij}(t)=\frac{(Y_{ij}(t)-Y_{ij}(t-1))}{(Y_{ij}(t)+Y_{ij}(t-1))}\times 200，t=2，3，\dots ，n$$
  当$Y_{ij}(t)$中有零或负值时，或者指标是比率序列是，取一阶差分：
$$C_{ij}(t)=Y_{ij}(t)-Y_{ij}(t-1)，t=2，3，\dots ，n$$
  为避免变动幅度大的指标在合成指数中取得支配地位，应标准化各指标的对称变化率$C_{ij}(t)$，使其平均绝对值等于1，计算标准化因子：
$$A_{ij}=\sum _{t=2}^n\frac{|C_{ij}(t)|}{(n-1)}$$
  标准变化率为：
$$S_{ij}(t)=\frac{C_{ij}(t)}{A_{ij}}，t=2，3，\dots ，n$$
  第二步、计算各指标组的标准化平均变化率
  令$R_j(t)，j=1，2，3$分别表示先行、一致、滞后指标组的平均变化率，
$$R_j(t)=\frac{{\sum }_{i=1}^{k_j}{S}_{ij}(t)\bullet w_{ij}}{{\sum }_{i=1}^{k_j}{w}_{ij}}，t=2，3，\dots ，n$$
  其中$w_{ij}$ 是第j组第i个指标的权重。
  由$R_j(t)$计算出指数标准化因子$F_j$：
$$F_j=\frac{\frac{{\sum }_{t=2}^n|R_j(t)|}{n-1}}{\frac{{\sum }_{t=2}^n|R_2(t)|}{n-1}}，j=1，2，3$$
  计算标准化平均变化率：
$$V_j(t)=R_j(t)/F_j，t=2，3，\dots ，n$$
  第三步、计算初始合成指数
  令$I_j(1)=100$，当上述指标取对称变化率时，计算初始合成指数：
$$I_j(t)=I_j(t-1)\times \frac{200+V_j(t)}{200-V_j(t)}，j=1，2，3，t=2，3，\dots ，n$$
  第四步、趋势调整并计算合成指数
  在初始合成指数基础上，对先行、一致和滞后三个指标组的标准化平均变化率$V_j(t)$进行趋势调整，使三个指标组得到的合成指数趋势与计算一致指标组中被采用的序列的趋势平均值一致。调整后的标准化平均变化率$V_j^{{}^{\prime }}(t)$，令$I_j^{{}^{\prime }}(1)=100$，则调整后的合成指数为：
$$I_j^{{}^{\prime }}(t)=I_j^{{}^{\prime }}(t-1)\times \frac{200+V_j^{{}^{\prime }}(t)}{200-V_j^{{}^{\prime }}(t)}，j=1，2，3，t=2，3，\dots ，n$$
  第五步、计算以基准年份为100的合成指数：
$$C{I}_j(t)=\frac{I_j^{{}^{\prime }}(t)}{\overline{I_j^{{}^{\prime }}}}\times 100$$
  其中$\overline{I_j^{{}^{\prime }}}$是$I_j^{{}^{\prime }}(t)$在基准年份的平均值。
3. 主成分分析法
  主成分分析(Principal Components Analysis)是利用降维的思想， 把多指标转化为少数几个合成指标的多元统计分析方法。在多元分析中， 为了尽可能完整地收集信息， 往往要取多个指标， 指标间存在一定的信息重叠。为降低问题的难度并剔除重叠的信息， 人们希望通过对原始指标进行线性组合得到新的、数量较少的合成指标， 来替代原始指标。为了使新的合成指标在最大程度上代表原始指标， 避免信息损失， 要求新的合成指标的方差最大。
  主成分分析数学模型如下：
  设有n个样品，每个样品观测p个指标（变量）：$X1，X2，\dots ，Xp$， 得到原始数据矩阵：
$$X=\left(\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1p}\\ x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right)$$
  其中，
$$X_i=\left(\begin{array}{c}{x}_{1i}\\ x_{2i}\\ ⋮\\ x_{ni}\end{array}\right)(i=1,2,\cdots ,p)$$
  用数据矩阵X的p个列向量（即p个指标向量）作线形组合（即综合指标向量）为：
$$\begin{gathered} F_1=a_{11}{X}_1+a_{21}{X}_2+\cdots +a_{p1}{X}_p \\ {F}_2=a_{12}{X}_1+a_{22}{X}_2+\cdots +a_{p2}{X}_p \\ ⋮ \\ {F}_p=a_{1p}{X}_1+a_{2p}{X}_2+\cdots +a_{pp}{X}_p \end{gathered}$$
  上述方程组要求：
$$a_{1i}^2+a_{2i}^2+\cdots +a_{pi}^2=1$$
  且系数αij由下列原则决定：
  ①、Fi与Fj（i≠j，i，j=1，…，p）不相关；
  ②、F1是X1，X2，…，Xp的一切线性组合（系数满足上述方程组）中方差最大的，F2是与F1不相关的X1，X2，…，Xp的一切线性组合中方差最大的，…，Fp是与F1，F2，…，$F_{p-1}$都不相关的X1，X2，…，Xp的一切线性组合中方差最大的。
  这样决定的综合变量F1，F2，…，Fp分别称为原变量的第一，第二，…，第p主成分，其中F1的方差在总方差中占的比例最大，其余主成分F2，F3，…，Fp的方差依次递减。在实际工作中挑选前几个甚至一个最大主成分F1，就能够基本包括全部指标所具有的信息，达到了将众多指标简化浓缩为少数几个甚至一个综合评价指标的目的。
  采用主成分方法来构建景气指数的步骤如下：
  第一步，按照主成分方法确定主成分个数。在已确定的全部p 个主成分中合理选择m 个来实现最终的评价分析。一般用方差贡献率${\alpha }_i$来确定最终的主成分个数。
$${\alpha }_i=\frac{{\lambda }_i}{{\sum }_{k=1}^p{\lambda }_k}\ge 0.8$$
  第二步，计算主成分权重。主成分的权重可为每个主成分的方差贡献率，即:
$${\omega }_i=\frac{{\lambda }_i}{{\sum }_{i=1}^p{\lambda }_i}$$
  第三步，计算主成分系数得分。根据各个主成分的系数得分，求出每个主成分的线性加权值:
$$F_i=u_{i1}{X}_1+u_{i2}{X}_2+\cdots +u_{ip}{X}_p$$
  第四步，计算初始景气指数。对m 个主成分进行线性加权，即得到初始的科技创新景气值:
$$F^{{}^{\prime }}=\sum _{i=1}^m{\omega }_i{F}_i$$
  第五步，调整数据，计算最终的景气值:
$$F=\frac{F_t^{{}^{\prime }}}{F_{t-1}^{{}^{\prime }}}\ast 100$$
4. S-W型景气指数法
  S-W型景气指数是在1988年由美国的斯托克和沃森提出的新型的景气指数方法。他们认为，景气循环，十分广泛的影响经济系统中的各个领域，相应的，各个领域中的景气波动也会综合导致总体经济的波动，因此，在这些领域波动的背后就有一个共同的驱动因素，这一共同的驱动因素是不可观测的用数学方法可以表示为一个基本变量，这个基本变量就代表了总的经济状态，也即它的循环就是真正的景气循环。这一基本变量就是S-W型景气指数，简称SW景气指数。SW景气指数与传统扩散指数、合成指数最大的不同就在于，SW指数的计算有着完善的理论基础和严密的数学模型支持，比传统的方法在逻辑严谨性上有了更进一步的发展。目前SW景气指数系统还在幵发阶段，虽然已经有少数机构开始尝试使用，但还不能完全取代合成指数CI。
  Stock和Watson认为经济变量所代表的真正的经济波动应该是去掉了趋势变动要素后的平稳部分。由于在这一平稳部分中还包含季节变动要素，所以还应从中除去季节变动要素。可以认为多个经济变量之间这种不含季节性变动的平稳部分的共同变动有着一个共同的因素，这一因素由一个单一的，不可观测的基本变量所体现。这一基本变量代表了总的经济状态，它的波动是真正的景气循环，并且被称为S-W景气指数。基于上述思想， Stock和Watson建立了一个随机模型，对这一不可观测的基本变量给出了数学定义。
  设$Y_t$为t时期n个经济变量的平稳部分(即去掉了趋势变动要素)的值， $Y_t$为n×1向量，它是可观测的，特别这里假定其季节变动要素已被消除。$C_t$为t时期的景气指数真值，它是一个标量，当$t=1，2，\dots ，T$时，它就是前述的S-W景气指数。它是不可观测的，必须对其进行推断。$u_t$是与$C_t$独立，表示各经济变旦随机变动的n×1向量，可假定$u_t$的期望值为0。以上各变量间满足关系式
$$Y_t=\beta +\gamma C_t+u_t\text{\hspace{1em}(1)}$$
  上式与通常的回归方程不同，因为作为说明变量的$C_t$本身是不可观测的，必须对其进行估计。这样的模型被称为UC模型。根据通常的回归方程式来估计是不可能的，必须利用状态空间模型。按状态空间模型的用语，上式称为测量方程，其中可以认为不含观测误差。
  其次，将$C_t$和$u_t$看成是随机过程，$C_t$为$AR(P)$(P阶自回归过程)， $u_t$的每一个分量为$AR(r)$，用式子表示即是
$$\Phi (L)C_t=\delta +{\eta }_t\text{\hspace{1em}(2)}$$
$$\Theta (L)u_t={\epsilon }_t\text{\hspace{1em}(3)}$$
  其中，
$$\Phi (L)=1-{\Phi }_{1}L-{\Phi }_2{L}^2-\dots -{\Phi }_p{L}^p$$
$$\Theta (L)=1-{\Theta }_{1}L-{\Theta }_2{L}^2-\dots -{\Theta }_r{L}^r$$
${\Theta }_i=diag({\theta }_{i1}，\dots ，{\theta }_{in})$，L为Lag算子，$L{C}_t=C_{t-1}$，$L{u}_t=u_{t-1}$。
  假定，${\eta }_t\backsim N(0，{\sigma }^2)；{\epsilon }_i\backsim N(0_n，{\sigma }^{2}H)$并且两者独立。其中，$H=diag(h_1，\dots ，h_n)$。
  按状态空间的说法，(2)式和(3)式称为迁移方程。
  与通常的回归方程式一样，在$Y_t$正规化条件下来推断参数$\gamma 、\Phi 、\theta 、{\sigma }^2、H$没有本质上的影响。此时(1)一(3)式成为
$$Y_t=\gamma C_t+u_t\text{\hspace{1em}(4)}$$
$$\Phi (L)C_t={\eta }_t\text{\hspace{1em}(5)}$$
$$\Theta (L)u_t={\epsilon }_t\text{\hspace{1em}(6)}$$
  将上述假定按状态空间模型的记号可表述如下。首先状态变量${\alpha }_t$为
$${\alpha }_t=[C_t{C}_{t-1}\dots C_{t-p+1}{u}_t\dots u_{t-r+1}{]}^T$$
  它是$(p+nr)\times 1$的向量。而观测方程，迁移方程和干扰项分别为
$$Y_t=Z{\alpha }_t\text{\hspace{1em}(7)}$$
$${\alpha }_t=X{\alpha }_{t-1}+{\xi }_t\text{\hspace{1em}(8)}$$
$${\xi }_t\backsim N(0_{n+1}，{\sigma }^2\sum )\text{\hspace{1em}(9)}$$
  其中，$Z=[\gamma 0_{n，P-1}{I}_n{0}_{n，r-1}]$

  $\sum$为对角阵，$\sum =diag(10_{p-1}^{{}^{\prime }}{h}_1{h}_2\cdots h_{n-1}{h}_n{0}_{(n-1)r}^{{}^{\prime }})$。
  S-W景气指数的计算步骤如下：
  第一步，用kalman滤波法估计状态空间模型的参数分布。
  在给定参数X，Z， ∑和延迟次数p，q，r之下利用kalman滤波反复计算${\alpha }_t$的分布，t-1期的${\alpha }_{t-1}$假定服从$N({\alpha }_{t-1}，{\sigma }^2{p}_{t-1})$。此时，${\alpha }_t$的分布按下式计算
$${\alpha }_{t|t-1}=X{\alpha }_{t-1}\text{\hspace{1em}(10)}$$
$$p_{t|t-1}=X{p}_{t-1}{X}^{{}^{\prime }}+\sum \text{\hspace{1em}(11)}$$
$$F_t=Z{p}_{t|t-1}{Z}^{{}^{\prime }}\text{\hspace{1em}(12)}$$
$${\alpha }_t={\alpha }_{t|t-1}+p_{t|t-1}{Z}^{{}^{\prime }}{F}_t^{-1}(Y_t-Z{\alpha }_{t|t-1})\text{\hspace{1em}(13)}$$
$$p_t=p_{t|t-1}-p_{t|t-1}{Z}^{{}^{\prime }}{F}_t^{-1}Z{p}_{t|t-1}\text{\hspace{1em}(14)}$$

  当初值${\alpha }_0$和$p_0$给定时，由(10)一(14)式可以计算出${\alpha }_t(t=l，2，\dots T)$的分布是$N({\alpha }_t，{\sigma }^2{p}_t)$。
  第二步，初值${\alpha }_0$和$p_0$的计算方法。
  方法1，在假定$Y_t$为平稳序列下($E{Y}_t$和$D{Y}_t$不依赖于t，从而$E({\alpha }_t)={\alpha }_0$和$D({\alpha }_t)={\sigma }^2{p}_0$不依赖于t)，由(8)式得到
$${\alpha }_0=x{\alpha }_0+E({\xi }_t)$$
  从而有：
$${\alpha }_0=[I-X{]}^{-1}E({\xi }_t)=0\text{\hspace{1em}(15)}$$
  再由(8)式得
$${\sigma }^2{p}_0={\sigma }^{2}X{p}_0{X}^{{}^{\prime }}$$
  从而有：
$$p_0-X{p}_0{X}^{{}^{\prime }}=\sum$$
  利用多元统计方法中的拉直运算，便得
$$Vec(p_0)-XO{X}^{{}^{\prime }}Vec(p_0)=Vec\sum$$
  从而有：
$$Vec(p_0)=(I-XO{X}^{{}^{\prime }}{)}^{-1}Vec\sum \text{\hspace{1em}(16)}$$
  方法2，将$Y_t$按时间的反序排列后记以$Y_t^{{}^{\prime \prime }}$(对原有的$Y_1$， $Y_2$，…，$Y_r$，取$Y_t^{{}^{\prime \prime }}$=$Y_r$ ，…，$Y_l^{{}^{\prime \prime }}$=$Y_{T-l+1}$，…$Y_T^{{}^{\prime \prime }}$=$Y_l$)。取${\alpha }_0^{{}^{\prime \prime }}$=0， $p_0^{{}^{\prime \prime }}$=$kI$(k充分大)，并按(10)一(14)式的Kalman滤波公式计算，最后得到的α和p就作为初值${\alpha }_0$和$p_0$，这种方法主要在$Y_t$并非平稳以及最初的$Y_t$看来可能为异常值时使用。
  第三步，参数估计
  以上的计算是在给定参数值之下进行计算的。假定已给定p，q，r，这些参数值可以按极大似然法求得。在计算(10)-(14)式的过程中，可求得预测误差
$$v_t=Y_t-Z{\alpha }_{t|t-1}\text{\hspace{1em}(17)}$$
  这是以$t-l$期信息预测$Y_t$时的误差。另一方面， $Y_t$的对数似然函数可用$t-l$期信息所得到的条件概率${\alpha }_t\backsim N({\alpha }_{t|t-1}，p_{t|t-1})$，从而$Y_{t}N(Z{\alpha }_{t|t-1}，F_t)，F_t=Z{p}_{t|t-1}{Z}^{{}^{\prime }}$表示为
$$log=\frac{1}{2Tnlog(2\pi )}+\sum _{t=1}^{T}log|F_t|+\sum _{t=1}^T{v}_t^{{}^{\prime }}{F}_t^{-1}{v}_t\text{\hspace{1em}(18)}$$
  记所求的参数向量为ψ，则
$$\begin{gathered} \psi =[h_1\cdots h_n{\gamma }_{11}{\gamma }_{21}\cdots {\gamma }_{n1}{\gamma }_{12}\cdots {\gamma }_{nq} \\ {\Phi }_1\cdots {\Phi }_p{\theta }_{11}{\theta }_{21}{\theta }_{n1}\cdots {\theta }_{nr}] \end{gathered}$$
  它是n(1+q+r)+p维向量。当γ和θ的延迟次数改变时，ψ的维数也随之变化。(18)式最大化的${\psi }^{\ast }$就是我们所要求的参数的估计值。此时ψ必须是定义ψ的参数空间的内点。实际上， ψ的参数空间是由扰动项的方差的非负性$(h_i>0，i=1，2，\cdots n)$，C的平稳性(Φ(L)的全部根在单位圆的外侧)，$u_i$的平稳性(θ(L)的全部根在单位圆的外侧)所构成的。因此， ψ的估计问题归结为在满足上述参数空间的内点解的约束条件下求使对数似然函数(18)最大化问题的解${\psi }^{\ast }$，${\psi }^{\ast }$就是ψ的估计值。${\psi }^{\ast }$计算出来后，Kalman滤波法的(10)-(14)式中的参数X，Z， ∑便给定了，从而利用Kalman滤波法可推断出SWI。
  第四步，最优估计量的计算。
  为求最大似然估计量，需要求解$\partial logL(\psi )/\partial \psi =0$。采用Taylor展式，取一次近似，可将$\partial logL(\psi )/\partial \psi$表示成

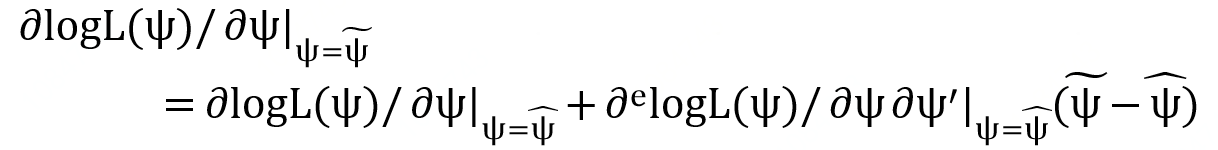
  令其为0，可得迭代公式：

  通过上式来求$\hat{\psi }{}^{\prime }$，其收敛值即为ψ的最优估计量。
  最后，关于p，q，r可用如下方法确定。对于各种组合(p，q，r)，在约束条件下求得使对数似然函数极大化的${\psi }^{\ast }(p，q，r)$及此时的对数似然函数值logL(${\psi }^{\ast }(p，q，r)$)。然后以logL(${\psi }^{\ast }(p，q，r)$) 作成准则进行评价以决定p，q，r的次数。这些准则包括似然比检验，AIC准则，BIC准则。

各类景气指数适用范围

1. 扩散类景气指数适用范围
  扩散指数有如下作用：
（1）确定经济运行阶段及走向
（2）扩散指数在每一个阶段停留的时间代表经济波动在此阶段的扩散速度，时间越长，扩散越慢。它在某一点的值，代表经济波动扩散的程度和范围。
（3）利用先行扩散指数、同步扩散指数和滞后扩散指数可预测和监控经济运行。
（4）可以研究经济总量的波动与同步扩散指数曲线之间的关系。
  扩散指数的缺陷：
  不能很好地反映出经济的上升和下降的程度，而只能反映上升或下降的方向及转折位置。因此，扩散指数还需要有其他方法与其结合运用。
  扩散指数适用范围：
  扩散指数的概念十分简单：在任一时间，一组特定的序列向上运动，而其余的序列则可能向下运动，如果向上运动的时间序列的数目所占比重大于(或小于)50%，则经济为扩张(或收缩)。
  在分析历史经济周期方面，扩散指数是一个有用的工具。它提供了在一组给定指标序列中有多少序列处于上升或下降趋势的信息，并显示了这个数目是如何随时间而变化的，因而扩散指数能较真实地反映在周期中各种经济活动是如何随时间扩散的。
  通常情况下，以调研问卷的形式构建的景气指数适合采用扩散指数法进行景气指数编制。除此之外，当指标体系中包含一定比例的定性指标或者离散型数据指标的情况下适合采用扩散指数法。
2. 合成指数适用范围
  合成指数亦称“景气综合指数”。由一类特征指标以各自的变化幅度为权数的加权综合平均数。即多个指标的加权平均。能预测经济周期波动的转折点，并能在某种意义上反映经济周期波动的振幅。但在景气转折点的判断方面无法显示经济各部门之间的经济波及、渗透程度。通常用该指标分析与过去比较、经济变动程度的大小及速度等量的方面的问题。
  合成指数适用于以连续型的行业宏观经济数据指标为基础的景气指数的编制，主要是通过对多个行业宏观指标变化率的综合，判定行业景气发展情况和趋势。目前，合成指数在景气指数编制中占据重要的位置，许多有巨大影响力的行业景气指数均采用合成指数法编制。
3. 主成分分析法适用范围
  综合景气指数是观测国民经济运行动向的重要指标，通常是通过把若干个宏观指标的单指数加权汇总得到，这种方法需要人为确定各单指标权重，计算结果带有主观因素。使用较多的指标进行描述使分析复杂化，难以对众多指标的影响作出正确的判断，需要少量几个“综合评价指标”。通过简单加权的合成方法，难以得到科学的结果。
  主成分分析是一种多元统计方法，可以将众多指标简化浓缩为少量几个甚至一个综合评价指标，使简化的指标既能基本包括全部指标具有的信息，又使指标之间相互无关，较好地解决了相似指标的多重共线性带来的指数误差。
  主成分分析法的优点是，可消除评价指标之间的相关影响、可减少指标选择的工作量、当评级指标较多时还可以在保留绝大部分信息的情况下用少数几个综合指标代替原指 标进行分析、在综合评价函数中，各主成分的权数为其贡献率，它反映了该主成分包含原始数据的信息量占全部信息量的比重，这样确定权数是客观的、合理的，它克服了某些评价方法中认为确定权数的缺陷。主成分分析法的缺点是主成分分析法在降维的同时降低了信息量，主成分的解释其含义一般多少带有点模糊性，不像原始变量的含义那么清楚、确切，这是变量降维过程中不得不付出的代价。
  主成分分析方法主要适用于连续型多指标构成的景气指数，在指标确定的情况下，使用主成分分析的方法将多个变量转化为少数几个综合变量（即主成分），其中每个主成分都是原始变量的线性组合，各主成分之间互不相关，从而这些主成分能够反映始变量的绝大部分信息，且所含的信息互不重叠。
4. S-W型景气指数适用范围
  S-W景气指数是利用时间序列分析方法，从多个重要经济序列中得到一个观测不到的变量，并把它视为真正的景气循环。由于S-W景气指数是建立在严密的数学模型基础上，所以它和CI、DI等传统的景气循环测定方法相比，有了理论模型基础上的进步。S-W景气指数的缺点是模型对指标及数据的要求较高，指标的选择需进行严格的筛选，指标数据需剔除增长因素和周期循环因素等。除此之外，通过S-W景气指数所得到一个观测不到的变量是否能够充分解释经济的景气程度，无法进行检验。

景气指数指标选取方法

1. 景气指数指标的分类
  确定经济周期波动的基准日期后将某个经济指标的周期波动于基准转折点相比，可根据其与基准指标（能敏感地反映当前经济活动的重要经济指标）的相互关系将景气指标分为先行、一致和滞后指标。
  （1）先行指标（Leading Indicators）
  先行指标是指在宏观经济波动达到高峰或低谷前，超前出现峰或谷的指标。通常，先行指标的峰或谷时点比基准循环时点超前3个月以上，且超前期相对稳定。先行指标具有先行性质主要有两方面的原因，一方面某些先行指标本身就是景气动向的预期指标（如中小企业状况的预期判断），另一方面某些经济活动在时间上比景气波动超前（如新招工人数、建筑开工面积）。
  （2）一致指标（Coincident Indicators）
  一致指标，又称同步指标，是指该指标达到高峰和低谷的时间和经济周期波动基准日期的时间大致相同，反映当前的景气变动状况。通常一致指标的时点与基准循环时点的时差保持在三个月以内。
  （3）滞后指标（Lagging Indicators）
  滞后指标是指高峰或低谷转折点滞后于经济周期波动基准转折点的指标。滞后指标的作用在于它的峰或谷的出现可以确认经济周期波动的高峰或低谷确已出现。滞后指标循环与基准循环的时差关系为滞后3个月以上，且滞后期相对稳定。
2. 景气指数指标的选取原则
  影响行业景气波动的因素众多，包括该行业的生产经营活动、相关行业经济活动及宏观经济、政治、社会等环境和政策因素。因此在筛选合适的景气指标建立景气指标初选池是应遵循以下原则：
  （1）经济重要性：所选景气指标具有经济意义，能够充分的代表该行业经济活动的某一方面。不是所有的指标都纳入指标体系中，否则会导致指标体系过于庞大，甚至出现信息重叠等问题；
  （2）统计充分性：所选指标的数据应当尽可能的完整可靠，通常选用月度或季度数据，并且数据区间较长较完整、覆盖面大、可信度高，样本容量充足；
  （3）统计适时性：所选指标的数据能及时定期地统计并公布，一般在每月（季）后的1至2个月（季度）内能使用；
  （4）时差对应性：所选指标的峰、谷应当与经济周期波动的基准日期的峰、谷有较稳定的对应关系（超前、一致或滞后）；
  （5）反映敏感性：所选指标必须能够敏感地反映经济波动，具有“指示器”、“报警器”作用。
3. 景气指数指标的选取方法
  （1）基准指标的选择。
  在景气波动分析中，基准指标是能够敏感反映当前经济活动的经济指标。常用的选择方法有四种：1、将GDP、CPI等能反映经济景气波动的重要经济指标作为基准指标；2、选取多个具有经济重要性并能同步反映经济景气波动的指标，将他们合成一个指数，作为基准指标；3、根据专家意见或专家评分选择基准指标；4、根据经济循环年表的方法来确定基准指标。
  （2）景气指数指标的选取方法。
  随着经济发展、统计体系及统计方法不断完善，统计指标的数目日趋庞大，从众多经济指标中筛选出适用且可靠地景气指标的常用方法主要有时差相关性分析、序列图示法、K-L信息量法、聚类分析、峰谷对应法和评分系统等。

  
  
  
All things are difficult before they are easy.