单变量线性回归
模型描述
让我们回顾上篇文章中的房价示例,现在我们有一批数据集,里面有房屋的尺寸以及房屋的价格,我们需要使用房屋的尺寸来预测房屋的价格。如下图:

现在我们考虑需要使用一个程序来通过房屋的大小预测出房屋的价格,房屋的大小是我们的参数(设为x),预测值是输出(设为y),我们称y=h(x)中映射关系h为一个假设函数。

如图所示,h就是代表假设函数。按照之前的例子,我们可以使用一个一元函数来表示我们的h(因为是线性回归,所以要使用线性函数),所以我们使用
h
(
x
)
=
θ
0
+
θ
1
x
h(x)=\theta{_0} + \theta{_1}x
h(x)=θ0+θ1x。我们的任务就是需要设置出一个算法,帮助我们找到我们的假设函数h。接下来我们来介绍一下怎么去找到这个
θ
0
\theta{_0}
θ0以及
θ
1
\theta{_1}
θ1。
代价函数
从上一个例子中来构建代价函数

如图所示,我们需要找到一个最能拟合所有数据集的一条直线,那我们可以通过计算每个点与我们的拟合直线之间的距离,当使这个距离之和为最小值的时候,我们就找到了最能够拟合我们数据集的一条直线。这个时候的两个参数,就是我们需要寻找的参数。
J ( θ 0 , θ 1 ) = 1 2 m ∗ ∑ i = 1 m ( y ( i ) − h ( x ( i ) ) ) 2 该公式为代价函数 J(\theta{_0},\theta{_1})=\frac 1 {2m}*\sum_{i=1}^{m} {(y{^{(i)}}-h(x{^{(i)}}))}^2 \text {该公式为代价函数} J(θ0,θ1)=2m1∗i=1∑m(y(i)−h(x(i)))2该公式为代价函数
这里的 x ( i ) x^{(i)} x(i)和 y ( i ) y^{(i)} y(i)所指的是对应的第 i i i个样本的 x x x与 y y y的值
上面的公式就是我们的代价函数,原理就我们的每一个预测值与数据集中的原本值进行相减再求平方,则计算出两点之间的距离平方,然后对其取平均。
代价函数的例子:
(1)将
θ
0
\theta{_0}
θ0设为0,此时学习算法的优化目标是通过
θ
1
\theta{_1}
θ1选择获得最小的
J
(
θ
1
)
J(\theta{_1})
J(θ1),minimize(
J
(
θ
1
)
J(\theta{_1})
J(θ1))就是线性回归的目标函数,最小化
J
(
θ
1
)
J(\theta{_1})
J(θ1)来找到一条最符合数据的直线。
(2)将
θ
0
\theta{_0}
θ0和
θ
1
\theta{_1}
θ1都考虑进来,得到一个3D曲面图如下:

横轴为
θ
0
\theta{_0}
θ0和
θ
1
\theta{_1}
θ1,若改变参数的值,会得到不同的
J
(
θ
0
,
θ
1
)
J(\theta{_0},\theta{_1})
J(θ0,θ1)。竖轴为曲面的高度,就是
J
(
θ
0
,
θ
1
)
J(\theta{_0},\theta{_1})
J(θ0,θ1)的值。这个类似碗的形状就是代价函数的形状。使用等高线图或称为等高图像展示这些曲面,通过这些图像,更好地理解代价函数J的意义,如何对应不同的假设函数以及接近代价函数J最小值的点,对应着更好的假设函数,同样,我们真正想要的是一个高效的算法自动寻找代价函数J的最小值对应的
θ
0
\theta{_0}
θ0和
θ
1
\theta{_1}
θ1。

梯度下降
梯度下降是一种可以将代价函数J最小化的算法,它不仅被用在线性回归上,还被广泛应用于机器学习的众多领域。
问题概述:
有一个函数,想要用一个算法求最小化函数
J
(
m
i
n
(
J
(
θ
0
,
θ
1
)
)
)
J(min(J(\theta{_0},\theta{_1})))
J(min(J(θ0,θ1)))
梯度下降思路(outline):
(1)给定θ0和θ1的初始值,通常将他们初始设为0。
(2)不停地一点点改变
θ
0
\theta{_0}
θ0和
θ
1
\theta{_1}
θ1来使
J
(
θ
0
,
θ
1
)
J(\theta{_0},\theta{_1})
J(θ0,θ1)变小,直到找到
J
J
J的最小值或局部最小值。
梯度下降的过程如下图:


就像下山一样,每次在一点环顾四周,往最陡峭的路向下走,用图形的方式更形象的表示。但如果你的起始点偏移了一些,会得到完全不同的局部最优解,就像上面图像所示,这就是梯度下降算法的一个特点。
梯度下降算法的数学定义如下:
θ i : = θ i − α ∂ ∂ θ i J ( θ 0 , θ 1 ) \theta{_i}:=\theta{_i}-{\alpha} {\frac \partial {\partial\theta{_i}}J(\theta{_0},\theta{_1})} θi:=θi−α∂θi∂J(θ0,θ1)
反复做上述这一步,直至收敛。
符号定义如下:
:=这个符号表示赋值运算符;α被称为学习速率,用来控制梯度下降时,即下山时该迈出多大的步子。
正确实现梯度下降的方法,即同步更新,如下所示:
t
e
m
p
0
:
=
θ
0
−
α
∂
∂
θ
0
J
(
θ
0
,
θ
1
)
temp0:=\theta{_0}-{\alpha} {\frac \partial {\partial\theta{_0}}J(\theta{_0},\theta{_1})}
temp0:=θ0−α∂θ0∂J(θ0,θ1)
t
e
m
p
1
:
=
θ
1
−
α
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
temp1:=\theta{_1}-{\alpha} {\frac \partial {\partial\theta{_1}}J(\theta{_0},\theta{_1})}
temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ
0
:
=
t
e
m
p
0
\theta{_0}:=temp0
θ0:=temp0
θ
1
:
=
t
e
m
p
1
\theta{_1}:=temp1
θ1:=temp1
这样就能够同步更新
θ
0
\theta{_0}
θ0和
θ
1
\theta{_1}
θ1,这是正确的实现方法。
根据α是学习速率,有以下结论:
1.如果α(学习速率)太小,则梯度下降法会收敛的很慢;
2.如果α太大,则梯度下降法每次下降很快,可能会越过最小值,最终会导致无法收敛甚至发散。
3.如果已经在局部最优点,θ1将不再改变,那么梯度下降法更新其实什么都没做,意味着它始终保持在局部最优值。
线性回归的梯度下降:
这一节中要将梯度下降和代价函数结合得到线性回归算法,它可以用直线模型来拟合数据。

这是梯度下降法和和线性回归模型(包括了假设函数和平方差代价函数)。
探讨梯度下降算法的导数项:
将上面的结果应用到梯度下降算法中,就得到了回归的梯度下降算法:
有时我们把这个算法也称为Batch梯度下降算法,每一步下降都遍历了整个训练集的样本。
这就是我们的第一个机器学习算法–线性回归算法。








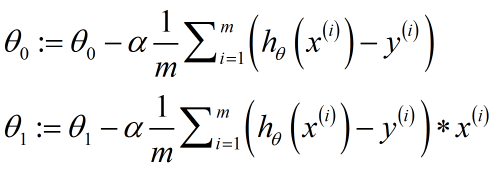














 1150
1150











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








