文章目录
1. 梯度下降简介
标量场的梯度是一个向量场,设标量场
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)
∇
f
=
(
∂
f
∂
x
,
∂
f
∂
y
,
∂
f
∂
z
)
\displaystyle \nabla f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})
∇f=(∂x∂f,∂y∂f,∂z∂f)标量在某一点的梯度指向在该点标量增长速度最快的方向,则标量沿某一点梯度反方向
−
∇
f
-\nabla f
−∇f在该点下降速度最快
设
λ
\lambda
λ为步长、学习率、学习速率
△ x i = − λ ∇ f \triangle x_i=-\lambda \nabla f △xi=−λ∇f
x i + 1 = x i + △ x i \displaystyle x_{i+1}=x_i+\triangle x_i xi+1=xi+△xi
2. 几种数据集训练方式
根据训练数据集的大小有三种训练方式
2.1 批量梯度下降法 BGD
batch gradient descent
-
优点:全局最优化
-
缺点:计算量大,迭代速度慢
2.2 随机梯度下降法 SGD
stochastic gradient descent
-
优点:训练速度快,支持在线学习
-
缺点:准确度降低,有噪音,非全局最优化
2.3 小批量梯度下降法 MBGD
mini-batch gradient descent
优点:计算小批量梯度更加高效,可以使用numpy库加速
缺点:准确度不如BGD,非全局最优解
MBGD 每次训练用训练集的一部分或者一小批,每次抽取样本数为k,k一般取10到500之间
MBGD算法实现
更新梯度:
g
^
←
1
b
a
t
c
h
s
i
z
e
∑
i
=
j
j
+
b
a
t
c
h
s
i
z
e
∇
θ
L
(
f
(
x
(
i
)
,
θ
)
,
y
(
i
)
)
\displaystyle \hat g \leftarrow \frac{1}{batchsize}\sum_{i=j}^{j+batchsize}\nabla_{\theta} L(f(x^{(i)},\theta),y^{(i)})
g^←batchsize1i=j∑j+batchsize∇θL(f(x(i),θ),y(i))
更新参数:
θ
←
θ
−
λ
g
^
\theta \leftarrow \theta - \lambda \hat g
θ←θ−λg^
3. 传统梯度优化的不足
-
传统的梯度优化对超参数比较敏感,过小会导致收敛过慢,过大会导致越过极值点
-
学习率容易在迭代过程中保持不变,很容易造成算法被卡在鞍点的位置,或者在比较平坦的区域,梯度接近0,优化算法往往误判,还未达到极值点,就提前结束迭代
4. 对传统梯度下降的优化
4.1 动量算法
学习率或者步长
λ
\lambda
λ不变,通过优化方向来对传统梯度下降优化
基本思想是一个物体在运动时具有惯性
动量算法每下降一步都是由前面下降方向的一个累计和当前点的梯度方向矢量求和
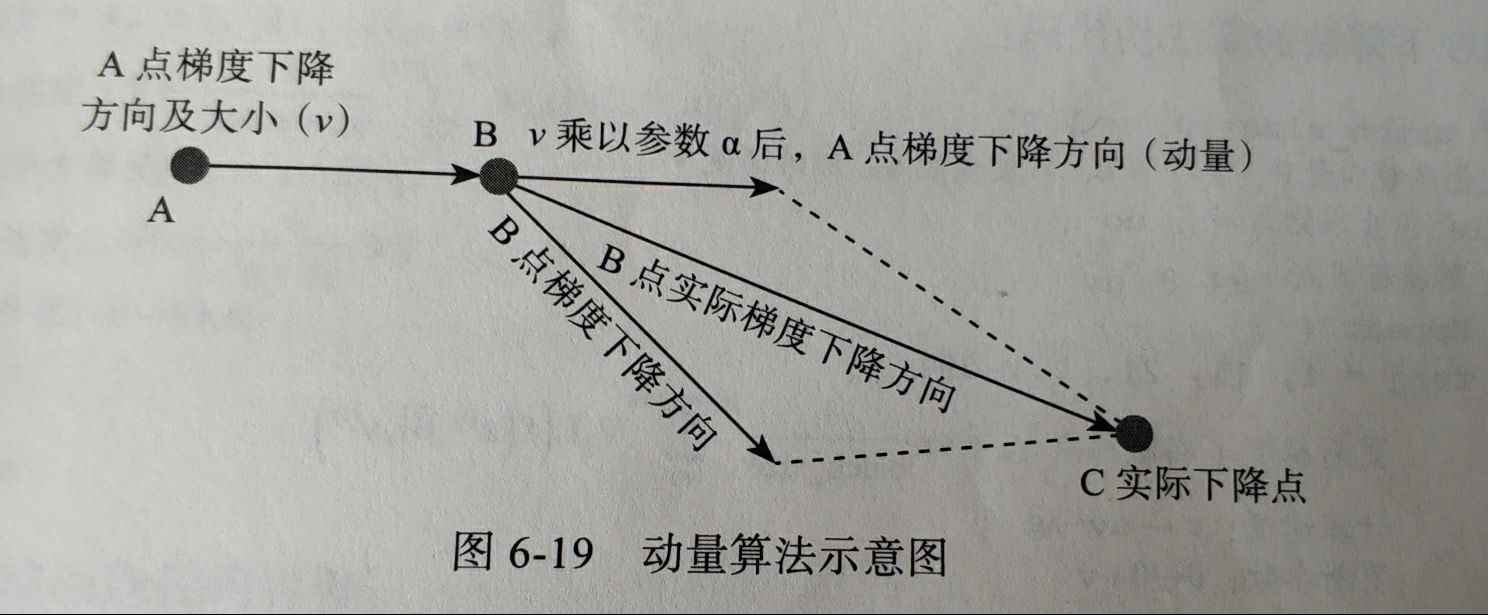
更新梯度: g ^ = 1 b a t c h s i z e ∑ i = j j + b a t c h s i z e ∇ θ L ( f ( x ( i ) , θ ) , y ( i ) ) \hat g =\displaystyle \frac{1}{batchsize}\sum_{i=j}^{j+batchsize}\nabla_{\theta}L(f(x^{(i)},\theta),y^{(i)}) g^=batchsize1i=j∑j+batchsize∇θL(f(x(i),θ),y(i))
计算速度: v = α v − λ g ^ v=\alpha v-\lambda \hat g v=αv−λg^
更新参数: θ = θ + v \theta=\theta + v θ=θ+v
4.2 自适应算法
4.2.1 AdaGrad
-
同时调整学习率和方向
-
对稀疏参数进行大幅更新和对频繁参数进行小幅更新
-
设积累平方梯度为 r r r,设小参数 δ \delta δ避免分母为0
更新梯度: g ^ = 1 b a t c h s i z e ∑ i = j j + b a t c h s i z e ∇ θ L ( f ( x ( i ) , θ ) , y ( i ) ) \hat g=\frac{1}{batchsize}\sum_{i=j}^{j+batchsize}\nabla_\theta L(f(x^{(i)},\theta),y^{(i)}) g^=batchsize1∑i=jj+batchsize∇θL(f(x(i),θ),y(i))
积累平方梯度: r = r + g ^ ⨀ g ^ r=r+\hat g\bigodot \hat g r=r+g^⨀g^
计算速度: △ θ = − λ δ + r ⨀ g ^ \triangle \theta=-\frac{\lambda}{\delta+\sqrt{r}}\bigodot \hat g △θ=−δ+rλ⨀g^
更新参数: θ = θ + △ θ \theta=\theta+\triangle \theta θ=θ+△θ
-
特点
(1):随着迭代时间增加,累计梯度r越大,从而学习率 λ δ + r \displaystyle \frac{\lambda}{\delta+\sqrt{r}} δ+rλ随时间增加而减少,在接近目标值时不会因为学习率过大而越过极值点
(2):不同参数之间学习速率不同,与前面固定学习率相比不容易在鞍点卡住
(3):如果梯度积累参数r比较小,则学习速率比较大;如果梯度积累参数r比较小,则学习率比较小
4.2.2 RMSProps
-
引入衰减速率$ \rho $
-
更新梯度: g ^ = 1 b a t c h s i z e ∑ i = j j + b a t c h s i z e ∇ θ L ( f ( x ( i ) , θ ) , y ( i ) ) \hat g=\frac{1}{batchsize}\sum_{i=j}^{j+batchsize}\nabla_\theta L(f(x^{(i)},\theta),y^{(i)}) g^=batchsize1∑i=jj+batchsize∇θL(f(x(i),θ),y(i))
积累平方梯度: r = ρ r + ( 1 − ρ ) g ^ ⨀ g ^ r=\rho r+(1-\rho)\hat g\bigodot \hat g r=ρr+(1−ρ)g^⨀g^
计算速度: △ θ = − λ δ + r ⨀ g ^ \triangle \theta=-\frac{\lambda}{\delta+\sqrt{r}}\bigodot \hat g △θ=−δ+rλ⨀g^
更新参数: θ = θ + △ θ \theta=\theta+\triangle \theta θ=θ+△θ
4.2.3 Adam
-
本质上是带有动量项的RMSProps
-
优点主要在经过偏置矫正后,每一次迭代学习速率都有一个确定范围,使得参数比较平稳
-
引入矩估计指数衰减速率 ρ 1 \rho_1 ρ1 、 ρ 2 \rho2 ρ2,初始化一阶和二阶矩变量 s = 0 , r = 0 s=0,r=0 s=0,r=0,t=0
-
更新梯度: g ^ = 1 b a t c h s i z e ∑ i = j j + b a t c h s i z e ∇ θ L ( f ( x ( i ) , θ ) , y ( i ) ) \hat g=\frac{1}{batchsize}\sum_{i=j}^{j+batchsize}\nabla_\theta L(f(x^{(i)},\theta),y^{(i)}) g^=batchsize1∑i=jj+batchsize∇θL(f(x(i),θ),y(i))
t ← t + 1 t\leftarrow t+1 t←t+1
更新有偏一阶矩估计 s = ρ 1 s + ( 1 − ρ 1 ) g ^ s=\rho_1s+(1-\rho_1)\hat g s=ρ1s+(1−ρ1)g^
更新有偏二阶矩估计 r = ρ 2 r + ( 1 − ρ 2 ) g ^ ⨀ g ^ r=\rho_2r+(1-\rho_2)\hat g\bigodot \hat g r=ρ2r+(1−ρ2)g^⨀g^
修正一阶矩偏差: s ^ = s 1 − ρ 1 t \hat s=\displaystyle \frac{s}{1-\rho_1^t} s^=1−ρ1ts
修正二阶矩偏差: r ^ = r 1 − ρ 2 t \displaystyle \hat r=\frac{r}{1-\rho_2^t} r^=1−ρ2tr
积累平方梯度: r = ρ r + ( 1 − ρ ) g ^ ⨀ g ^ r=\rho r+(1-\rho)\hat g \bigodot \hat g r=ρr+(1−ρ)g^⨀g^
参数更新: △ θ = − λ s ^ δ + r ^ \displaystyle \triangle\theta=-\lambda\frac{\hat s}{\delta+\sqrt{\hat r}} △θ=−λδ+r^s^
4.3 有约束最优化
4.3.1 等式约束最优化
m
i
n
f
(
x
)
min\ f(x)
min f(x)
s
.
t
.
h
(
x
)
=
0
s.t.\ h(x)=0
s.t. h(x)=0
采用拉格朗日乘子法
4.3.2 不等式最优化
m
i
n
f
(
x
)
min\ f(x)
min f(x)
s
.
t
.
h
(
x
)
<
=
0
s.t.\ h(x)<=0
s.t. h(x)<=0
先求出 h(x)<0的条件下的极值
然后再用拉格朗日乘子法求出h(x)=0条件下的极值
两者比较 求出极大值或者极小值




















 4128
4128











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








