图像傅里叶变换：从空域转换到频域（包含频谱图分析、简单带阻滤波器理解）

2021年10月21日10:24:05
占坑，这周五图像处理课讲完PPT后填。
2021年10月22日21:07:55 -> 讲课完毕

数字图像处理、图像恢复，噪声去除PPT

图像处理课课件，包含图像恢复、噪声去除部分内容及相关注解
链接: https://pan.baidu.com/s/1wBfXM0ZrSw3O221GUShVtw  密码: 424w
--来自百度网盘超级会员V5的分享

分割线

---

说明：在准备课件上台讲解的时候，为去除周期性噪声，需在频域上进行操作；所以在网上查看了许多视频博客知乎等，有了初步的理解，现在将收集的资料整理出来，并发布到博客，在网上参考的地方，我会一一给出参考，方便其它同学快速理解将图像从空域到频域转换的这个过程，也提供一些比较好的博文及视频，希望能对你有参考作用！

---

1、图像空域到频域的转换

以下内容来自BILIBILI的一个非常棒的视频：《P04 图像的快速傅里叶变换及其应用，作者：flybirdAI》

说明：图像和公式来自此视频中的截图，此视频讲的非常的好，清晰明了，对于空域到频域的转换，不涉及代码的话看前28分钟就足够了！

频域变换一般过程：

原图->DFT/FFT(正变换)->中心化->频域显示(处理)->去中心化->IDFT/IFFT(反变换)->原图

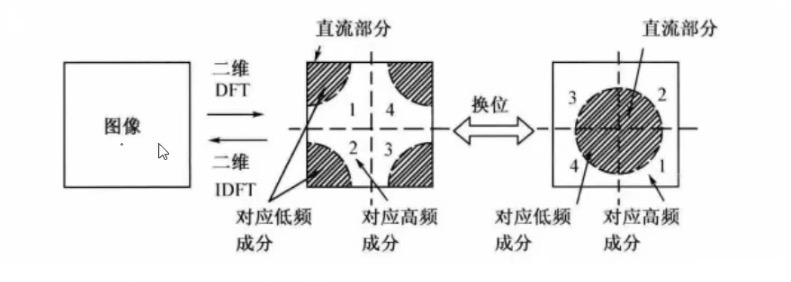
图像高频：亮度或灰度变化激烈的部分，如边缘和轮廓
图像低频：变化不大或变化较为平缓的地方，如大块的结构

DFT（离散傅里叶变换）：Discrete Fourier transform
FFT（快速傅里叶变换）：Fast Fourier transform

二维图像（M行N列）
正变换：
$$F(u,v)=\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y)e^{-j2\pi (ux/M+vy/N)}$$

反变换：$$f(x,y)=\frac{1}{MN}\sum _{u=0}^{M-1}\sum _{v=0}^{N-1}F(u,v)e^{j2\pi (ux/M+vy/N)}$$

其中下式为欧拉公式：
$$e^{j\theta }=\cos (\theta )+j\sin (\theta )$$

频域分析就是对F(u，v)进行操作：

由于共轭对称性：可对FFT变换的结果再进行FFT变换得到IFFT（I指的是反变换，IFFT反快速傅里叶变换，将图像从频域转换到空域）

注：傅里叶谱通过对log(1+F|(u,v)|)表示，另外自行频率分析时，也往往将频率窗口移动窗口中心处。

FFT还可以做卷积：

1. 将图像和卷积模板都进行正变换到频率域
2. 将两者在再频域直接进行相乘运算
3. 再反变换到空间域作为输出

频域变换过程时刻牢记下图：

---

分割线

如果深入理解后，可以观看3Blue1Brown的视频：【官方双语】形象展示傅里叶变换

---

2、代码实现傅里叶变换

代码：【原文博客：python的numpy库和cv2库实现图像傅里叶变换】

# writer:wojianxinygcl@163.com

# date  : 2020.3.30 

# 原文地址 : https://www.cnblogs.com/wojianxin/p/12530172.html


import cv2
import numpy as np
from matplotlib import pyplot as plt


def fft_cv(img):
    """
    用cv进行傅里叶变换
    :param img:
    :return:
    """

    # 傅里叶变换

    dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)

    dftshift = np.fft.fftshift(dft)

    res1 = 20 * np.log(cv2.magnitude(dftshift[:, :, 0], dftshift[:, :, 1]))

    # 傅里叶逆变换

    ishift = np.fft.ifftshift(dftshift)

    iimg = cv2.idft(ishift)

    res2 = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])

    # 显示图像

    plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original Image')

    plt.axis('off')

    plt.subplot(132), plt.imshow(res1, 'gray'), plt.title('Fourier Image')

    plt.axis('off')

    plt.subplot(133), plt.imshow(res2, 'gray'), plt.title('Inverse Fourier Image')

    plt.axis('off')

    plt.show()


def fft_numpy(img):
    """
    用numpy对图像进行傅里叶变换
    """
    # 傅里叶变换

    f = np.fft.fft2(img)

    fshift = np.fft.fftshift(f)

    res = np.log(np.abs(fshift))

    # 傅里叶逆变换

    ishift = np.fft.ifftshift(fshift)

    iimg = np.fft.ifft2(ishift)

    iimg = np.abs(iimg)

    # 展示结果

    plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original Image')

    plt.axis('off')

    plt.subplot(132), plt.imshow(res, 'gray'), plt.title('Fourier Image')

    plt.axis('off')

    plt.subplot(133), plt.imshow(iimg, 'gray'), plt.title('Inverse Fourier Image')

    plt.axis('off')

    plt.show()


if __name__ == '__main__':
    # 读取图像
    img = cv2.imread('LENA256.BMP', 0)  # 读取灰度图
    fft_numpy(img)  # 使用numpy进行变换
    # fft_cv(img)   # 使用cv进行变化

Lena标准测试图: https://pan.baidu.com/s/1FGAYFsNaPR7XuKbL6aTnhQ  密码: m19a
--来自百度网盘超级会员V5的分享

结果：

---

3、如何分析频谱图，知识点总结：

参考以下博客：

1. 【傅里叶分析之掐死教程（完整版）更新于2014.06.06】
2. 【通俗讲解：图像傅里叶变换】
3. 【傅立叶变换频谱图怎么看？cccw的问题回答】
   

我的总结：

1.图2是转换到频域二维可视化的结果，称作频谱图

2.由于频谱动态范围很大，所以用log变换降低频谱的动态范围

3.图1为空域：f(x, y) , 图2为频域：H(u, v)，中心化之后的结果，频谱图的正中心点为H（0，0），图像大小与原图相同

4.图1和图2相同位置的点没啥直接的对应关系，右边的每一个点可以理解为所描述的是一种平面波，它是构成左边图无数个波面中的一个，它与左边的每一个点都相关

一个曲面可以有很多个正弦平面波组成，二维正弦平面波，可以用以下4个参数来描述它：频率、幅度、相位、方向

所有波都可以用多个正弦波叠加；波又可以通过频率、幅值和方向来表示（频谱图中相位信息被舍弃）

5.图2中的每一个点：
它到中点的距离描述的是频率
中点到它的方向是构成平面波的方向
那一点的灰度值描述的是它的幅值

6.频谱图里面描述的信息有：频率f，振幅A，方向n

7.每一个频谱图中的点它不是实数，是一个虚数，a+bi，为二维可视化，计算的是它的绝对值

8.点点越亮代表这个数值越大，点点越暗代表这个数值越小（幅值的大小）

---

2021年11月02日16:35:09===========================带通/带阻滤波器===========================

带通/带阻滤波器

如下图所示，左图是被周期性正弦噪声所污染的图像，右图是去噪后的结果，想要在空域去除这样的噪声是很困难的，但是在频域上确能很轻松的进行操作。

带阻滤波器可以移除图像中特定的频率范围，从而很轻松的去除周期性噪声。

简单解释带阻滤波器以及带通滤波器：

• 带阻滤波器：带阻，阻就是阻止，阻止特定的频率范围通过
• 带通滤波器：带通，通就是通过，只允许特定的频率范围通过

由上简单的定义可知，带阻滤波器和带通滤波器可以相互转换，是一种互补的关系，带阻滤波器取反就是带通滤波器，带通滤波器取反就是带阻滤波器。

理想的带阻滤波器定义如下：

$$H(u,v)=\{\begin{array}{ll}1& \text{ if }D(u,v)<D_0-\frac{W}{2}\\ 0& \text{ if }{D}_0-\frac{W}{2}\le D(u,v)\le D_0+\frac{W}{2}\\ 1& \text{ if }D(u,v)>D_0+\frac{W}{2}\end{array}$$
【参考博客】：数字图像处理与python实现-带通滤波器
带阻滤波器，如下图3（第二排第一个），理想的带阻滤波器的定义如上，D(u,v)为频域中任意一点到中心点的距离，D0代表带阻滤波器的半径（从中心到带阻滤波器第一个内圈和第一个外圈之间的中间位置），W代表带阻滤波器的带宽（内圈到外圈的距离），上述公式代表的就是带阻滤波器，含义就是带阻滤波器带宽范围内的部分：不允许它通过，带阻滤波器带宽范围外的地方保持不变，可视化的结果如下图3。

图像从上到下，从左到右分别表示图1：周期性正弦噪声污染的图像；图2：图1转换的频域的结果；图3：理想带阻滤波器；图4：在频域去除周期性噪声后转换到空域的结果

如何使用带阻滤波器

1. 将图像1转换到频域，如图2，图1周期性正弦噪声在频域可视化的结果，表现在图2上就是围绕中心一圈分布均匀亮亮的8个小点点
2. 去掉周期性噪声，就是去掉这些小点点
3. 设计合适的带阻滤波器，如图3，黑色部分设为0，白色部分设为1，与图2的大小相同，两幅图像进行哈达玛积（对应点相乘）->得到结果（带阻滤波器带宽上的点都被置为0了，周期性噪声点在带宽内也被置为0，消除掉了）
4. 然后将第三步去噪后的结果，通过IFFT反快速傅里叶变换还原到空域，得到最终结果图4