最短路径（Shortest Paths）

最短路径

最短路径（Shortest Paths）

最短路径问题一直是图论研究的热点问题。例如在实际生活中的路径规划、地图导航等领域有重要的应用。关于求解图的最短路径方法也层出不穷，本篇文章将详细讲解图的最短路径算法。最短路径问题的背景问题一般是类似：已知各城市之间距离，请给出从城市A到城市B的最短行车方案 or 各城市距离一致，给出需要最少中转方案。简而言之：固定起始点的情况下，求最短路。

引子

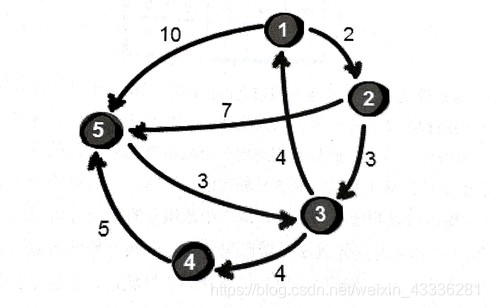
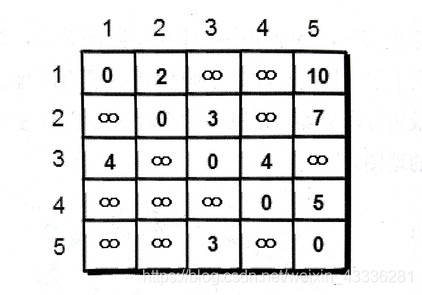
下面这个例子，有向带权图，我们用邻接矩阵存储图信息，求解任意两点间的最短路径。

Floyd-Warshall算法

我们来想这么一个逻辑：对于i、j两个节点，如果想让路径变短，只能通过第三个节点k来中转。从 1->5 距离为10，但 1->2->5 距离变成9了。事实上，**每个顶点都有可能使另外两个顶点间的路程变短，**这种通过中转变短的操作叫做松弛。

Code

Floyd-Warshall算法的原理是动态规划，我们来看它的代码：

def FloydWarshall(graph):
    n = len(graph)
    distance = [[graph[i][j] for j in range(n)] for i in range(n)]
    precursor = [[i if graph[i][j] not in [float("inf"), 0] else float("inf") for j in range(n)] for i in range(n)]

    for k in range(n):
        for i in range(n):
            for j in range(n):
                if i != j and i != k and j != k and distance[i][j] > distance[i][k] + distance[k][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]
                    precursor[i][j] = precursor[k][j]  # i -> j 更新为 i -> k -> j，j 的前驱节点更新为原来 [k][j] 位置

    return distance, precursor

三层循环，第一层循环中间点k，第二、第三层循环起点、终点i、j，算法的思想很容易理解：如果i到k的距离加上k到j的距离小于原先i到j的距离，那么就用这个更短的路径长度来更新原先i到j的距离。我们可以来使用一下：

    graphData = [[0, 2, float("inf"), float("inf"), 10],
                 [float("inf"), 0, 3, float("inf"), 7],
                 [4, float("inf"), 0, 4, float("inf")],
                 [float("inf"), float("inf"), float("inf"), 0, 5],
                 [float("inf"), float("inf"), 3, float("inf"), 0]]

    shortest, path = FloydWarshall(graphData)
    for item in shortest:
        print(item)
    print()
    for item in path:
        print(item)

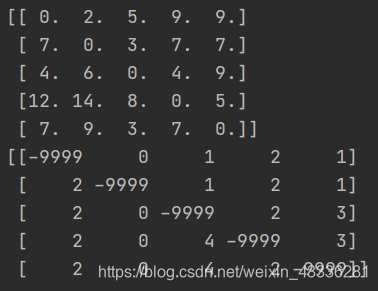
在SciPy中有一个官方提供的floyd_warshall函数，我们可以通过调用它来验证一下我们写的floydWarshall算法是否正确。有些不同的地方是，在SciPy的floyd_warshall函数中如果点i和j之间不存在路径，则前导[i，j]=-9999。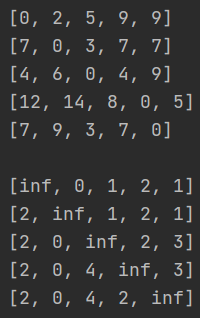

复杂度分析

Floyd-Warshall算法的时间复杂度为O(N3)，空间复杂度为O(N2)。

Dijkstra算法

有的时候我们可能只想找到从原点到某个顶点的最短路径，比如我们打车的时候查地图，就只需要知道从我当前位置到目的地的最短路径就可以了。Dijkstra算法是用来计算从一个点到其它所有点的最短路径问题，是一种单源最短路径算法，也就是说，只能计算起点只有一个的情况。
对于图G=<V, E>上带权的单源最短路径问题，Dijkstra算法设置一个集合S用来记录已经求得最短路径的顶点，初始时把起点v放入S中，集合S每并入一个新顶点v，都要修改原点v到集合V-S中顶点的当前最短路径长度值。

Code

Dijkstra算法是基于贪心策略的，我们来看它的代码：

def Dijkstra(graph, node):
    n, queue, visit = len(graph), list(), set()
    heapq.heappush(queue, (0, node))
    distance, precursor = [float("inf") for _ in range(n)], {node: None}
    distance[node] = 0

    while queue:
        dist, vertex = heapq.heappop(queue)
        visit.add(vertex)

        for i in range(n):
            val = graph[vertex][i]
            if val != float("inf") and val not in visit and dist + val < distance[i]:
                precursor[i] = vertex
                distance[i] = dist + val
                heapq.heappush(queue, (dist + val, i))

    return distance, precursor

我们来分析一下这个算法，从起点到一个顶点的最短路径一定会经过至少一个“中转点”（我们认为起点也是一个“中转点”），如果我们想要求出起点到一个顶点的最短路径，那我们必须要先求出从起点到中转点的最短路径。
对于图G=<V, E>，将所有的点分为两类，一类是已经确定最短路径的点，称为“白点”，另一类是未确定最短路径的点，称为“蓝点”。如果我们要求出一个点的最短路径，就是把这个点由蓝点变为白点，从起点到蓝点的最短路径上的中转点在这个时刻只能是白点。
Dijkstra算法的思想：首先将起点的距离标记为0，而后进行n此循环，每次找出一个到起点距离最短的点，将它从蓝点变为白点，随后枚举所有的蓝点，如果以此白点为中转到达某个蓝点的路径更短的话，那么就更新。我们可以来使用一下：

    graphData = [[0, 2, float("inf"), float("inf"), 10],
                 [float("inf"), 0, 3, float("inf"), 7],
                 [4, float("inf"), 0, 4, float("inf")],
                 [float("inf"), float("inf"), float("inf"), 0, 5],
                 [float("inf"), float("inf"), 3, float("inf"), 0]]

    shortest, path = Dijkstra(graphData, 0)
    print(shortest, path)

在SciPy中有一个官方提供的dijkstra函数，我们可以通过调用它来验证一下我们写的Dijkstra算法是否正确。


注意：Dijkstra算法不能处理存在负边权的情况。

复杂度分析

时间复杂度为O(V)。

Bellman-Ford+SPFA算法

Bellman-Ford算法与Dijkstra算法类似，都以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解。在两个算法中，计算时每个边之间的估计距离值都比真实值大，并且被新找到路径的最小长度替代。
　Bellman - Ford算法基于动态规划，反复用已有的边来更新最短距离，Bellman-Ford算法的核心就是松弛。简单地对所有边进行松弛操作，共|V|-1次，其中|V|是图中顶点的数量。对于点 v 和 u，如果 dist[u] 和 dist[v] 满足 dist[v] > dist[u] + map[u][v]，那么dist[v] 就应该被更新为 dist[u] + map[u][v]。反复地利用上式对每条边进行松弛，从而更新 dist[] 数组，如果没有负权回路的话，应当会在 n - 1 次松弛之后结束算法。
SPFA是Bellman-Ford算法的一种队列实现，减少了不必要的冗余计算，它的主要思想是：初始时将起点加入队列，每次从队列中取出一个元素，并对所有与它相邻的点进行修改，若某个相邻的点修改成功，则将其入队，直到队列为空时算法结束。

Code

def spfa(graph, node):
    n, queue = len(graph), deque()
    queue.append((0, node))
    distance, precursor = [float("inf") for _ in range(n)], [float("inf") for _ in range(n)]
    distance[node] = 0

    while queue:
        pair = queue.popleft()
        dist, vertex = pair

        for i in range(n):
            val = graph[vertex][i]
            if val != float("inf") and dist + val < distance[i]:
                precursor[i] = vertex
                distance[i] = dist + val
                queue.append((dist + val, i))

    return distance, precursor

我们同样也通过scipy提供的bellman_ford函数来验证一下：

    graphData = [[0, 2, float("inf"), float("inf"), 10],
                 [float("inf"), 0, -3, float("inf"), 7],
                 [4, float("inf"), 0, 4, float("inf")],
                 [float("inf"), float("inf"), float("inf"), 0, 5],
                 [float("inf"), float("inf"), 3, float("inf"), 0]]

    shortest, path = spfa(graphData, 0)
    print(shortest, path)

    print('-' * 75)

    graphData = csr_matrix(graphData)
    distMatrix = bellman_ford(csgraph=graphData, directed=True, indices=0, return_predecessors=True)
    print(distMatrix)

注意：Bellman-Ford算法不能处理存在负权回路的情况。

复杂度分析

时间复杂度为O(kE)，k是常数，平均值为2，E是边数。

练习题

中等

LeetCode 1631. 最小体力消耗路径
POJ 1062.昂贵的聘礼

困难

LeetCode 778. 水位上升的泳池中游泳