深度学习中常用损失函数对比

损失函数大致可分为两种：回归损失（针对连续型变量）和分类损失（针对离散型变量）。

一、回归损失

L1 Loss

也称为Mean Absolute Error，即平均绝对误差（MAE），它衡量的是预测值与真实值之间距离的平均误差幅度，作用范围为0到正无穷。

公式为

优点：L1损失函数的主要特点是对异常点具有较好的鲁棒性。它通过计算预测值和真实值之间差的绝对值来度量误差，并且对所有误差平等对待，因此对于异常点的敏感性较低。这使得L1损失函数在处理包含离群点的数据时，能够避免模型受到这些点的过度影响。

缺点：由图可知其在0点处的导数不连续，使得求解效率低下，导致收敛速度慢；而对于较小的损失值，其梯度也同其他区间损失值的梯度一样大，所以不利于网络的学习。

L2 Loss

L2 Loss也称为均方误差（MSE），是指模型预测值f(x)和真实值y之间差值平方的平均值，公式如下：

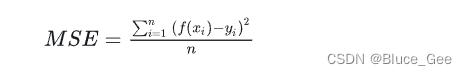
优点：函数曲线连续，处处可导，随着误差值的减小，梯度也减小，有利于收敛到最小值。

缺点：由于采用平方运算，当预测值和真实值的差值大于1时，会放大误差。尤其当函数的输入值距离中心值较远的时候，使用梯度下降法求解的时候梯度很大，可能造成梯度爆炸（反向传播中梯度累积导致的梯度非常大，甚至溢出NAN）。同时当有多个离群点时，这些点可能占据Loss的主要部分，需要牺牲很多有效的样本去补偿它，所以MSE损失函数受离群点的影响较大。

Smooth L1 Loss

还有一种平滑版的L1 Loss （Smooth L1 Loss），公式为

这个函数实际上是一个分段函数，它在[−1,1][−1,1]区间内使用L2损失（平方损失），而在[−1,1][−1,1]区间外使用L1损失（绝对值损失）。这种设计使得平滑L1损失在误差较小时能够保持梯度较小，而在误差较大时能够限制梯度的大小，从而在一定程度上避免了梯度爆炸的问题。

• 相比于L1 Loss，可以收敛得更快。
• 相比于L2 Loss，对离群点、异常值不敏感，梯度变化相对更小，训练时不容易跑飞。

所以在目标检测的Bounding box回归上早期会考虑Smooth L1 Loss

参考