梯度、散度和旋度大揭秘

一、基本概念理解

1、方向导数：在函数定义域内的点，对某一方向求导得到的导数。
2、梯度：是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值。
3、通量：在流体运动中，单位时间内流经某单位面积的某属性量，是表示某属性量输送强度的物理量。
4、环量：一个矢量沿一条封闭曲线积分。譬如在流场中任取一条封闭曲线，速度沿该封闭曲线的线积分称为该封闭曲线的速度环量。就像力做功的计算方法一样，形象地称速度环量为速度绕封闭曲线的速度功。
5、散度（divergence）可用于表征空间各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。当div F>0 ，表示该点有散发通量的正源（发散源）；当div F<0 表示该点有吸收通量的负源（洞或汇）；当div F=0，表示该点无源。
6、旋度是向量分析中的一个向量算子，可以表示三维向量场对某一点附近的微元造成的旋转程度。 这个向量提供了向量场在这一点的旋转性质。旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴，它和向量旋转的方向满足右手定则。旋度向量的大小则是绕着这个旋转轴旋转的环量与旋转路径围成的面元的面积之比。
7、对散度的理解
散度不为零说明场是有源场，电场有源无旋，磁场无源有旋。电场是由于分离电荷的存在而产生的，所以有源；但磁场目前还没有发现磁单极，所以无源。
8、对旋度的理解
俗话说有图有真相，我们看图说话！

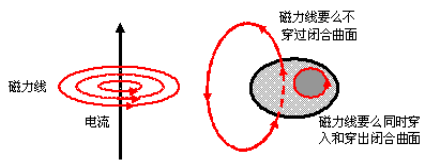
我的理解是会“旋转”，是因为受力不均匀所导致。如第一张图水流的例子，水流在垂直的上下平面上大小是相同的，所以左边不产生涡旋。右边里面会产生涡旋，是因为受力不均匀，在垂直的上下这个平面上，越往下，力越小，所以产生了涡旋。

二、梯度、散度和旋度的本质和联系

1、作用对象、运算对象和结果

梯度
作用对象：标量场
运算对象：标量
运算结果：向量（矢量）
散度
作用对象：向量场
运算对象：向量
运算结果：标量
旋度
作用对象：向量场
运算对象：向量
运算结果：向量

1.梯度针对一个标量场（势场），衡量一个标量场的变化方向。梯度为0说明该势场是个等势场。其结果为向量。

2.散度针对一个向量场，衡量一个向量场的单位体积内的场强。散度为0说明这个场没有源头。其结果为标量。

3.旋度针对一个向量场，衡量一个向量场的自旋。旋度为0说明这个场是个保守场（无旋场），保守场一定是某个标量场的梯度场。其结果为矢量。

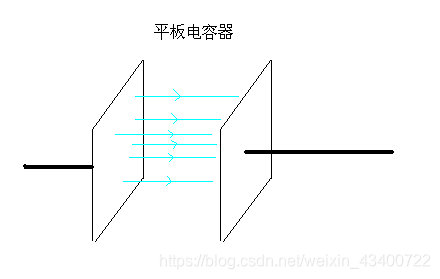
2、图解 任何标量场的梯度的旋度为0

如下图，电容器内部的电场，其实也就是梯度。对每个垂直方向的平面来说，电势位相等。所以，这就好比刚才水流的那个例子，上下来说受力相等，所以旋度为零。

3、电磁场中散度与旋度的求解

在电磁场中任一点处
（1）（▽·E）电场强度的散度==该点处自由电荷的体密度与介电常数之比。

（2）（▽xE）电场强度的旋度== 该点处磁感应强度变化率的负值。

（3）（▽·B）磁感应强度的散度 == 处处等于零。

（4）（▽xB）磁感应强度的旋度 == 该点处电流密度与磁导率的乘积。

（5）（▽·D）电位移的散度== 该点处自由电荷的体密度 .

（6）（▽xH）磁场强度的旋度 == 该点处传导电流密度与位移电流密度 的矢量和。

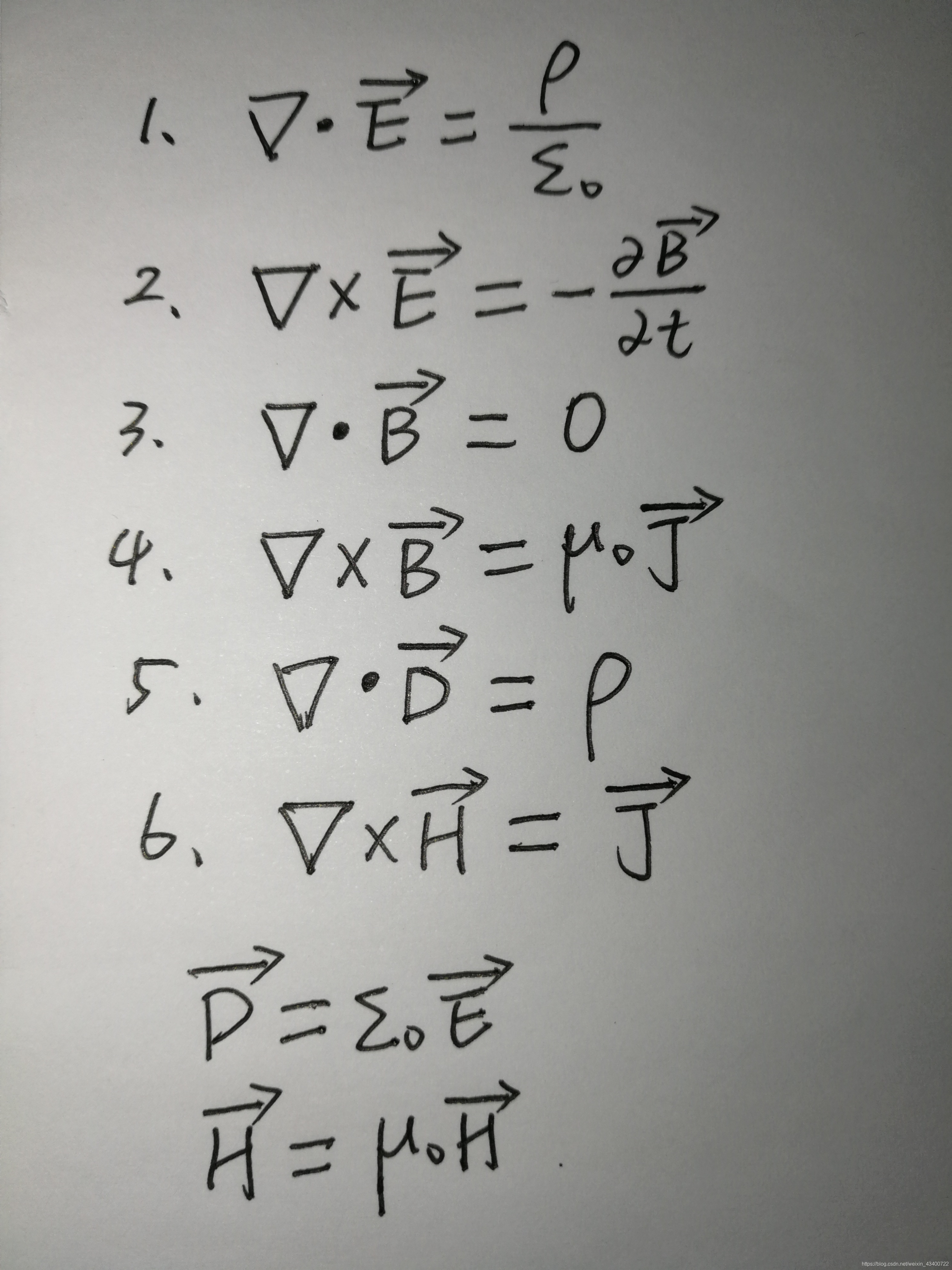
注释：
E 是电场强度矢量
B 是磁感应强度矢量
D 是电位移矢量（也叫电感应强度） 应该还有一个电传导向量 E=D+?
H 是磁场强度矢量 H=B+?
其中内在的联系是：
D=εE
B=μH
大写字母都是矢量

4、场的分类

向量场A，数量场u
▽称为汉密尔顿算子—— ▽·▽=▽2=△
△称为拉普拉斯算子。
1.梯度的旋度▽×▽u=0
梯度场的旋度为0，故梯度场是保守场（无旋场、有势场）。例如重力场。
2.旋度的散度▽·(▽×A)=0
旋度场的散度为0，故旋度场是无源场。例如磁场，磁场本身是其他场的旋度场。

特别说明一下，匀强场是保守场，磁场本身是有旋度的。因此绝对的匀强磁场是不可能的。

拉普拉斯算子△就是偏偏x，偏偏y，偏偏z；拉普拉斯算子是n维欧几里德空间中的一个二阶微分算子，定义为散度。

托克斯公式斯托克斯公式是格林公式的推广。格林公式表达了平面闭区域上的二重积分与其边界曲线上的曲线积分之间的关系。斯托克斯公式则把曲面上的曲面积分与沿着的边界曲线的曲线积分联系起来。