梯度、散度、旋度

梯度的$Jacobian$（Hession矩阵）、散度和旋度以及梯度的散度 $Laplacian$

1 基本概念

设向量$\mathbf{v}$如下:
$$\mathbf{v}=\left[\begin{array}{c}2x+3y\\ 2y+3z^3\\ 3z^2+y^2\end{array}\right]\begin{array}{c}(\mathbf{i})\\ (\mathbf{j})\\ (\mathbf{k})\end{array}$$

其中$\mathbf{i},\mathbf{j},\mathbf{k}$分别为$x,y,z$轴的单位列向量.

定义$\nabla$算子
$$\nabla =\left[\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}\end{array}\right]\begin{array}{c}(\mathbf{i})\\ (\mathbf{j})\\ (\mathbf{k})\end{array}$$

$\mathbf{v}$的$Jacobian$
$$\begin{array}{rl}\mathbf{v}{\nabla }^{\mathrm{T}}& =\left[\begin{array}{c}2x+3y\\ 2y+3z^3\\ 3z^2+y^2\end{array}\right]\left[\begin{array}{ccc}\frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\end{array}\right]\\ & =\left[\begin{array}{ccc}2& 3& 0\\ 0& 2& 9z^2\\ 0& 2y& 6z\end{array}\right]\end{array}$$
$\mathbf{v}$的散度
$$\nabla \cdot \mathbf{v}={\nabla }^{\mathrm{T}}\mathbf{v}=(2+2+6z{)}_{(标量)}$$
注意：因为$tr(AB)=tr(BA)$，所以$\mathbf{v}$的$Jacobian$的迹等于$\mathbf{v}$的散度.

$\mathbf{v}$的旋度
$$\begin{array}{rl}\nabla \times \mathbf{v}& =\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ 2x+3y& 2y+3z^3& 3z^2+y^2\end{array}\right|\\ & =(2y-9z^2)\mathbf{i}+0\mathbf{j}+(-3)\mathbf{k}\end{array}$$
$\mathbf{v}$的旋度的散度
$$\begin{array}{rl}\nabla \cdot (\nabla \times \mathbf{v})& ={\nabla }^{\mathrm{T}}(\nabla \times \mathbf{v})\\ & =\left[\begin{array}{ccc}\frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\end{array}\right]\left[\begin{array}{c}2y-9z^2\\ 0\\ -3\end{array}\right]\\ & =0_{(标量)}\end{array}$$

2 举例

自然可以想到，如果$\mathbf{v}$可以是某个函数的梯度(并不是任意的$\mathbf{v}$都可以是某函数的梯度，上述的$\mathbf{v}$就是个反例)，那么梯度的$Jacobian$、散度和旋度会有什么性质.

假设$f(x,y,z)=x+2y^2+3z^3$，则$f$的梯度$\nabla f$如下
$$\nabla f=\left[\begin{array}{c}\frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y}\\ \frac{\partial f}{\partial z}\end{array}\right]=\left[\begin{array}{c}1\\ 4y\\ 9z\end{array}\right]\begin{array}{c}(\mathbf{i})\\ (\mathbf{j})\\ (\mathbf{k})\end{array}$$

梯度$\nabla f$的$Jacobian$($Hession$矩阵$H(f)$)
$$\begin{array}{rl}H(f)& =\left[\begin{array}{ccc}\frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial x\partial y}& \frac{{\partial }^{2}f}{\partial x\partial z}\\ \frac{{\partial }^{2}f}{\partial y\partial x}& \frac{{\partial }^{2}f}{\partial y^2}& \frac{{\partial }^{2}f}{\partial y\partial z}\\ \frac{{\partial }^{2}f}{\partial z\partial x}& \frac{{\partial }^{2}f}{\partial z\partial y}& \frac{{\partial }^{2}f}{\partial z^2}\end{array}\right]\\ & =(\nabla f){\nabla }^{\mathrm{T}}\\ & =\left[\begin{array}{c}1\\ 4y\\ 9z^2\end{array}\right]\left[\begin{array}{ccc}\frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\end{array}\right]\\ & =\left[\begin{array}{ccc}0& 0& 0\\ 0& 4& 0\\ 0& 0& 18z\end{array}\right]\end{array}$$
梯度$\nabla f$的散度 $Laplacian$($L(f)$)
$$\begin{array}{rl}L(f)& =\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}+\frac{{\partial }^{2}f}{\partial z^2}\\ & ={\nabla }^{\mathrm{T}}(\nabla f)\\ & =\left[\begin{array}{ccc}\frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\end{array}\right]\left[\begin{array}{c}1\\ 4y\\ 9z^2\end{array}\right]\\ & =(0+4+18z{)}_{(标量)}\end{array}$$
可见，$tr(H(f))=L(f)$ .

梯度的旋度恒为$0$ （标量场梯度无旋，电场、重力场等保守场）
$$\begin{array}{rl}\nabla \times (\nabla f)& =\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ 1& 4y& 9z^2\end{array}\right|=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]\\ & =0\end{array}$$
梯度的旋度的散度恒为$0$ （矢量场旋度不散，磁场）
$$\begin{array}{rl}\nabla \cdot (\nabla \times (\nabla f))& ={\nabla }^{\mathrm{T}}(\nabla \times (\nabla f))\\ & =\left[\begin{array}{ccc}\frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]\\ & =0_{(标量)}\end{array}$$
虽然是从具体的例子得出的结论，但并不失一般性，可推广到高维.具体证明需要用到高斯定理、格林公式或斯托克斯公式等.

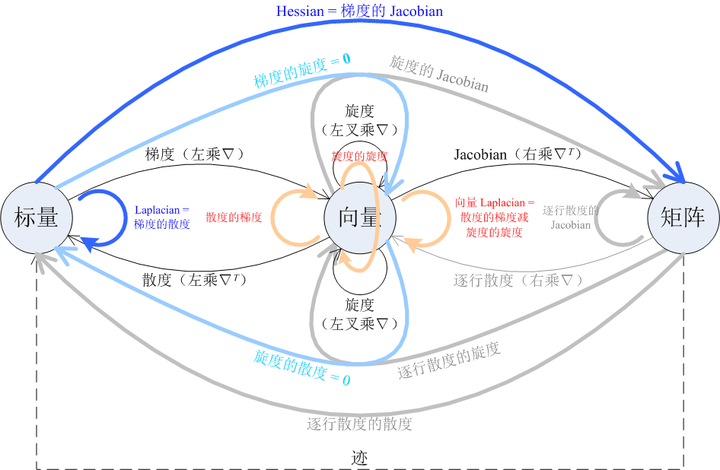
梯度、散度、旋度、Jacobian、Hessian、Laplacian 的关系图