深刻理解贝叶斯理论（数学图形可视化）

贝叶斯(Bayes)公式如下：

实例： A是一个温顺而又井井有条的人，他需要什么事情都有条理，且热衷于钻研细节。那你觉得A是图书馆管理员的概率大？还是认为A是农民的概率大？

心理学分析：当人们看到A是一个“温顺而又井井有条的人”后，大多数人认为一个温顺而又井井有条的人很大概率是一位图书馆管理员。毕竟相较于农民，这些特征更符合图书馆管理员的形象。但是心理学家认为这是“非理性”的。因为在做判断的时候，没人把农民和图书馆管理员的比例信息考虑在内。

下面从样本图形的角度进行分析，看看我们如何做出更准确的判断。假设，该国的农民与图书馆管理员的比例是20:1。同时，我们还了解不同身份下性格的统计信息，即40%的图书馆管理员符合“温顺而又井井有条的人”这一描述，而农民中只有10%符合“温顺而又井井有条的人”这个描述。当我们的总样本为10个管理员与200个农民时，那意味着有4（10*40%）位管理员与20位农民（200*10%）满足“温顺而又井井有条的人”的描述。其样本图例如图1所示。紫色圆形代表管理员，绿色圆形则代表农民。被橙色框选的管理员（4人）满足“温顺而又井井有条的人”的描述，被粉色框选的农民（20人）也满足“温顺而又井井有条的人”的描述。那么，当你听到一个人符合“温顺而又井井有条的人”这个描述时，实际的样本空间发生了变化，变成了24（4+20）人。

图1 样本图形

此时，从所有满足这个描述的人群中随便抽，他是图书馆管理员的概率为：

所以即使你认为符合这个描述的人是一个图书馆管理员的可能性是一个农民的4倍，也抵不过农民数量多。

所以贝叶斯理论的核心结论是：新证据不能直接凭空地决定你的看法，而是应该更新你的先验看法（之前的经验）。（后面对先验概率、后验概率，似然概率等概念进行描述）

上述理解过程可以分解为图中的三个步骤。

图2 概率的求解过程

理解了上述案例后，我们需要将其计算过程抽象为一个数学公式，也就是把210人的样本空间抽象为一个概率空间，且概率空间面积为1。抽象过程如下图3所示。

图3 贝叶斯定理的图形化抽象过程

我们继续对图3进行讲解，首先我们有一个假设P(H)，它代表不考虑任何证据的情况下，从样本中选定为管理员的可能性。术语P(H)称为先验概率。

下一个相关概率为管理员中符合描述的比例，即P(E|H) ，在贝叶斯定理中，称为“可能性”，高大上一点就是“似然概率”。符号（|）代表在H存在的情况下E发生的概率。

同样地，我们还需要考虑事物的另外一面（或者称为假设的对立面），也就是假设不正确的时候，在不考虑任何证据的情况下，假设不成立的概率可以表示为P(¬H)，符号（¬）代表“非”。

此时，在假设不正确的时候，我们能够看到证据的概率为P(E|¬H) 。

别忘了，我们想要计算的是：当我们看到证据的时候，假设正确的概率。可以理解为“温顺而又井井有条的人”这个描述存在的情况下，这个人是管理员的概率，数学表述为：P(H|E)  。术语P(H|E)称为后验概率。也就是看到证据后，假设的更新概率。

有了上述数学概念后，我们再重新计算一下上面讲解过的这个公式：

此时，我们已经知道P(是管理员|符合描述) 就是贝叶斯公式中的后验概率：P(H|E)。其详细计算过程可以表示如下：

           

            

            

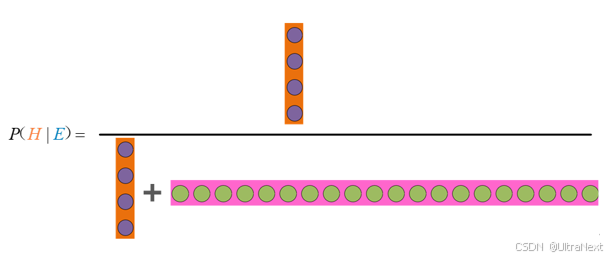
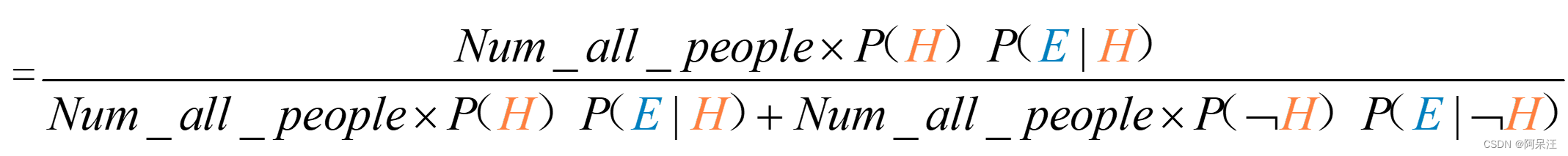
上式中，P(E) 为看到所有证据的概率，在上述例子中，P(E) =24/210。在实际计算过程中，是要将其拆分为假设成立与假设不成立两个部分进行计算，也就是P(H)*P(E|H) +P(¬H) *P(E|¬H) 。

收工，当你不会写贝叶斯公式的时候，画出下面这张图，相信你就能够立马写出来了。

  最后，贝叶斯公式还可以写为：

式中，P(E|H)/P(E)可以看作为对先验概率P(H)的更新系数。

上述贝叶斯公式可视化的思想借鉴于以下网页，感谢他们对数学可视化所作贡献。建议读者观看原版作者的可视化视频，能够理解得更加深刻。

参考来源为B站UP主：3Blue1Brown

网址：https://www.bilibili.com/video/BV1R7411a76r/?spm_id_from=333.999.0.0&vd_source=3ef125ad0d080f704e475bc4edef2340