MATLAB插值函数

正仪

已于 2024-01-07 00:26:43 修改

阅读量7k

点赞数 23

文章标签： matlab

于 2024-01-06 23:33:08 首次发布

本文链接：https://blog.csdn.net/weixin_43509834/article/details/135432129

版权

本文详细介绍了MATLAB中的各种插值函数，包括interp1、interp2、interpn和griddata，以及griddedInterpolant和scatteredInterpolant类。讨论了不同插值方法的适用场景，如线性、最近邻、自然样条和三次样条，并通过实例展示了插值函数的使用和效果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、MATLAB插值函数概览

1）本节重点介绍的插值函数

MATLAB插值函数	适用情况	基础句式
interp1 函数	interp1 主要用于一维数据的插值	interp1(x, y, x_interp, ‘linear’); 其中 x 和 y 是已知数据点，x_interp 是要插值的目标点。
interp2 函数	interp2 用于在二维平面上进行插值。适用于网格化的数据。	interp2(X, Y, Z, X_interp, Y_interp, ‘linear’); 其中 X、Y、Z 是已知数据网格，X_interp 和 Y_interp 是要插值的目标点。
interpn 函数	多维插值，适用于处理高维数据。	interpn(X1, X2, …, V, Xq1, Xq2, …);
griddata 函数	griddata 用于在不规则的数据点上进行插值，支持生成二维或高维的插值结果。适用于处理散乱的数据。	interp_values = griddata(x, y, z, x_interp, y_interp, ‘linear’); 其中，x、y、z 是已知的数据点和值。x_interp、y_interp 是要插值的目标点。
griddedInterpolant 类	griddedInterpolant 类是 MATLAB 中用于多维数据插值的类。这个类提供了一种高效的方法来进行插值，特别适用于规则网格上的数据，是 interp1、interp2、interp3 的通用化。（区别：griddedInterpolant 类适用于规则网格上的数据，也就是说，输入的坐标 X 应该是一个多维的规则网格，而 griddata 函数适用于不规则的或者散乱的数据点，坐标信息 x、y 可以是任意形状。）	F = griddedInterpolant(X, V, method); Vq = F(Xq); 其中，X：规则网格上的坐标信息，可以是一个多维数组，表示每个维度上的坐标。V：规则网格上对应坐标的值，与 X 的大小应该一致。method：插值方法，可以是 ‘linear’、‘nearest’、‘cubic’ 等。 Xq：待插值点的坐标，可以是一个数组或多维数组。
scatteredInterpolant 类	scatteredInterpolant 类提供了更灵活的方式进行不规则数据点的插值，支持多种插值方法。适用于处理不规则或散乱的数据点，类似于 griddata 但提供更多的控制选项。	F = scatteredInterpolant(x, y, z, ‘linear’); interp_values = F(x_interp, y_interp); 其中，x、y、z 是已知的数据点和值。x_interp、y_interp 是要插值的目标点。F 对象通过指定的插值方法进行插值。

2）MathWorks官网给出的其他插值函数：

网页链接： MathWorks-插值简介

二、插值方法

1）scatteredInterpolant 类

scatteredInterpolant 类支持的插值方法包括：

‘linear’（线性插值）（默认）
适用于大部分情况，计算较快。对于不规则分布的数据点，表现良好。
‘nearest’（最近邻插值）
适用于数据点分布较密集的情况。插值结果可能较粗糙。
‘natural’（自然样条插值）
适用于平滑数据，对非线性特征有较好的适应性。

网页链接： Mathworks-scatteredInterpolant函数

2）griddata 函数

‘linear’（线性插值）
适用于大部分情况，计算较快。线性插值在不规则数据点上表现良好，但对于数据的非线性特征可能表现不佳。
‘nearest’（最近邻插值）
适用于数据点分布较密集的情况。插值结果可能较粗糙。
‘natural’（自然样条插值）
适用于平滑数据，对非线性特征有较好的适应性。
‘cubic’（三次样条插值）
适用于平滑数据，对非线性特征有较好的适应性。计算相对较慢。
‘v4’（Vandermonde 插值）
适用于一维数据的插值。对于不规则分布的数据，可能表现不如其他插值方法。

网页链接： Mathworks-griddata 函数

三、插值代码实战

1）scatteredInterpolant 函数实战

针对下述相同的原始数据，采用 scatteredInterpolant 函数的不同插值方法（‘linear’、‘nearest’、‘natural’），进行对比。

原始数据

x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);
v = sin(x).^4 .* cos(y);
F = scatteredInterpolant(x,y,v);
[xq,yq] = meshgrid(-3:0.1:3);

‘nearest’方法代码：

F.Method = 'nearest';
vq1 = F(xq,yq);
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq1)
title('Nearest Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘nearest’运行结果：

‘linear’方法代码：

F.Method = 'linear';
vq2 = F(xq,yq);
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq2)
title('Linear')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘linear’运行结果：

‘natural’方法代码：

F.Method = 'natural';
vq3 = F(xq,yq);
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq3)
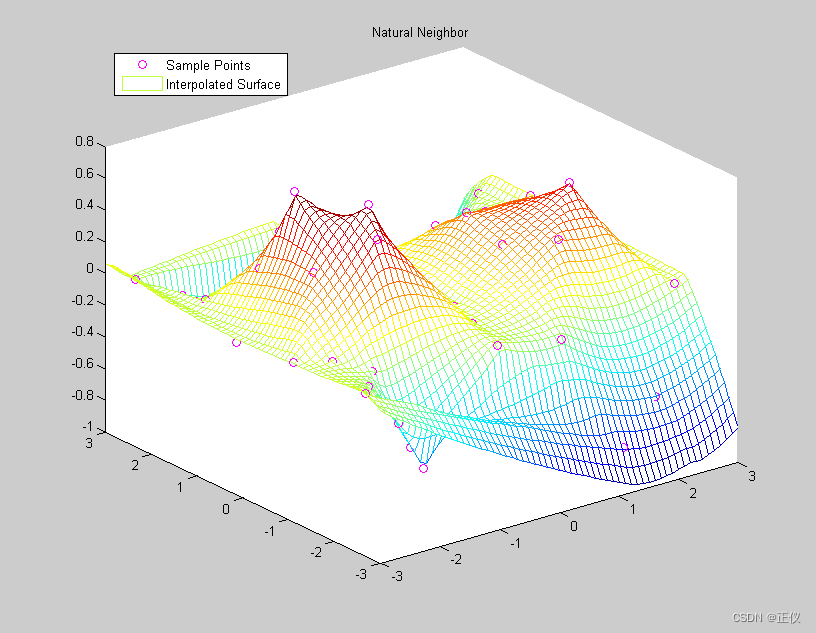
title('Natural Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘natural’运行结果：

绘制精确解。

figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,sin(xq).^4 .* cos(yq))
title('Exact Solution')
legend('Sample Points','Exact Surface','Location','NorthWest')

对比可知，这三种插值方法，性能都一般。

2）griddata 函数实战

针对下述相同的原始数据，采用 griddata 函数的不同插值方法（‘linear’、‘nearest’、‘natural’、‘cubic’），进行对比。

原始数据

x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);
v = sin(x).^4 .* cos(y);
[xq,yq] = meshgrid(-3:0.1:3);

‘nearest’方法代码：

z1 = griddata(x,y,v,xq,yq,'nearest');
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,z1)
title('Nearest Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘nearest’运行结果：

‘linear’方法代码：

z2 = griddata(x,y,v,xq,yq,'linear');
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,z2)
title('Linear')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘linear’运行结果：

‘natural’方法代码：

z3 = griddata(x,y,v,xq,yq,'natural');
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,z3)
title('Natural Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘natural’运行结果：

‘cubic’方法代码：

z4 = griddata(x,y,v,xq,yq,'cubic');
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,z4)
title('Cubic')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

‘cubic’运行结果：

绘制精确解。

figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,sin(xq).^4 .* cos(yq))
title('Exact Solution')
legend('Sample Points','Exact Surface','Location','NorthWest')