栈及其应用

栈的各种实现

栈是一种LIFO的结构，是一种特殊的线性表，其插入(也称入栈或压栈)和删除(出栈或弹栈)操作都在表的同一端进行。这一端成为栈顶，另一端称为栈底。

#ifndef STACK_H_INCLUDED
#define STACK_H_INCLUDED
using namespace std;
template<class T>
class stack{
public:
    virtual ~stack(){}
    virtual bool empty()const = 0;
                //当且仅当栈为空时返回true
    virtual int size() const = 0;
                //返回栈中元素个数
    virtual T& top() = 0;
                //返回栈顶元素的引用
    virtual void pop() = 0;
                //删除栈顶元素
    virtual void push(const T& theElement) = 0;
                //将元素theElement压入栈顶
};

#endif // STACK_H_INCLUDED

因为栈是一种插入和删除操作都被限制在一端进行的线性表，可以直接使用数组的派生类来实现，将入栈和出栈操作都放在数组的一端来进行。

// array stack derived from arrayList
// derives from abstract class stack just to make sure
// all methods of the ADT are implemented

#ifndef derivedArrayStack_
#define derivedArrayStack_

#include "arrayList.h"
#include "stack.h"
#include "myExceptions.h"

using namespace std;

//使用private，arrayList的公有和保护性方法以及数据成员
//都是类derivedArrayStack可以访问的
template<class T>
class derivedArrayStack : private arrayList<T>,
                          public stack<T>
{
   public:
      derivedArrayStack(int initialCapacity = 10)
        : arrayList<T> (initialCapacity) {}
      bool empty() const
           {return arrayList<T>::empty();}
      int size() const
          {return arrayList<T>::size();}
      T& top()
         {
            if (arrayList<T>::empty())
               throw stackEmpty();
            return get(arrayList<T>::size() - 1);
         }
      void pop()
           {
              if (arrayList<T>::empty())
                 throw stackEmpty();
              erase(arrayList<T>::size() - 1);
           }
      void push(const T& theElement)
           {insert(arrayList<T>::size(), theElement);}
};

#endif

但是以数组表示的线性表实现的话，在T是基本类型时，复杂度为O(1)，在T是用户定义的类型时位O(initialCapacity)。

// array implementation of a stack
// derives from the ADT stack

#ifndef arrayStack_
#define arrayStack_

#include "stack.h"
#include "myExceptions.h"
#include "changeLength1D.h"
#include <sstream>


template<class T>
class arrayStack : public stack<T>
{
   public:
      arrayStack(int initialCapacity = 10);
      ~arrayStack() {delete [] stack;}
      bool empty() const {return stackTop == -1;}
      int size() const
          {return stackTop + 1;}
      T& top()
         {
            if (stackTop == -1)
               throw stackEmpty();
            return stack[stackTop];
         }
      void pop()
           {
              if (stackTop == -1)
                 throw stackEmpty();
              stack[stackTop--].~T();  // destructor for T
           }
      void push(const T& theElement);
   private:
      int stackTop;         // current top of stack
      int arrayLength;      // stack capacity
      T *stack;           // element array
};

template<class T>
arrayStack<T>::arrayStack(int initialCapacity)
{// Constructor.
   if (initialCapacity < 1)
   {ostringstream s;
    s << "Initial capacity = " << initialCapacity << " Must be > 0";
    throw illegalParameterValue(s.str());
   }
   arrayLength = initialCapacity;
   stack = new T[arrayLength];
   stackTop = -1;
}

template<class T>
void arrayStack<T>::push(const T& theElement)
{// Add theElement to stack.
   if (stackTop == arrayLength - 1)
      {// no space, double capacity
         changeLength1D(stack, arrayLength, 2 * arrayLength);
         arrayLength *= 2;
      }

   // add at stack top
   stack[++stackTop] = theElement;
}
#endif

在arrayStack中，栈底元素就是stack[0]，栈顶元素就是stack[stackTop]。
这里arrayStack的性能>STL的stack>derivedArrayStack，因为STL的stack类不允许指定初始容量，因此改变数组大小的操作在所难免。
下面使用链表描述的stack类

// linked implementation of a stack
// derives from the ADT stack

#ifndef linkedStack_
#define linkedStack_

#include "stack.h"
#include "chainNode.h"
#include "myExceptions.h"
#include <sstream>

using namespace std;

template<class T>
class linkedStack : public stack<T>
{
   public:
      linkedStack(int initialCapacity = 10)
            {stackTop = NULL; stackSize = 0;}
      ~linkedStack();
      bool empty() const
           {return stackSize == 0;}
      int size() const
          {return stackSize;}
      T& top()
         {
            if (stackSize == 0)
               throw stackEmpty();
            return stackTop->element;
         }
      void pop();
      void push(const T& theElement)
           {
              stackTop = new chainNode<T>(theElement, stackTop);
              stackSize++;
           }
   private:
      chainNode<T>* stackTop;  // pointer to stack top
      int stackSize;           // number of elements in stack
};

template<class T>
linkedStack<T>::~linkedStack()
{// Destructor.
   while (stackTop != NULL)
   {// delete top node
      chainNode<T>* nextNode = stackTop->next;
      delete stackTop;
      stackTop = nextNode;
   }
}

template<class T>
void linkedStack<T>::pop()
{// Delete top element.
   if (stackSize == 0)
      throw stackEmpty();

   chainNode<T>* nextNode = stackTop->next;
   delete stackTop;
   stackTop = nextNode;
   stackSize--;
}
#endif

栈的应用

括号匹配

我们要做的是：对一个字符串的左右括号进行匹配。例如，字符串(a*(b+c)+d)在位置0和3有左括号，在位置7和10有右括号匹配。字符串(a+b))(中，位置5的右括号没有与之匹配的左括号。位置6的左括号没有与之匹配的右括号。

void printMatchedPairs(string expr)
{
	arrayStack<int> s;
	int length = (int)expe.size();
	
	//扫描表达式expr寻找左括号和右括号
	for(int i = 0; i < length;i++)
		if(expr.at(i) == '(')
			s.push(i);
		else
			if (expr.at(i) == ')')
		try
			{//从栈中删除匹配的左括号
				cout << s.top() << ' ' << i << endl;
				s.pop();//没有栈匹配
			}
			catch(stackEmpty)
			{//栈为空，没有匹配的左括号
				cou << "No match for right parenting"
					<<" at " << i << endl;			
			}
	while(!s.empty())
	{
		cout << "No match for left parenthesis at "
			<< s.top() << endl;
		s.pop();
	}
}

汉诺塔

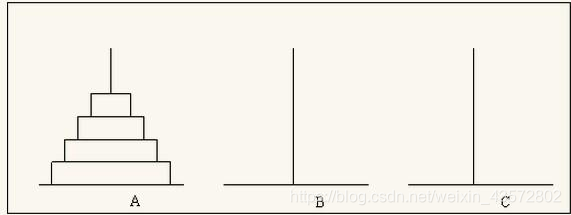
假设有4个碟子和三座塔。初始时所有碟子从大到小堆在塔A上，我们要把碟子都移动到塔B，每次移动一个，而且任何时候都不能把大碟子压在小碟子上。

递归

一个简洁的解决方法是递归，为了把最大的碟子移到塔B的底部，必须把其余n-1个碟子移到,C，然后把最大的碟子移到塔B。为了把n-1个碟子移到塔C，需要先把第n-1个碟子移到C，因此，必须先把n-2个碟子移到B……依次递归。实例说明，上图中，为了把底部的4号移到B，必须先把1~3号移到C，为了把3号移到C，必须把1~2移到B，为了把2移到B，必须把A移到C。这是把4号移到B的步骤，然后接下来就是把C中n-1个碟子移到B。C++代码如下
推出递归关系后，就直接从n=1开始推递推的代码

void HanoiTower(int n,int A,int B,int C)
{//把塔A的n个碟子移动到塔B
 //用塔C作为中转地
  	if(n > 0){
  		HanoiTower(n-1,A,C,B)
 		cout << "move top disk frow tower " << A
 	  	 	<< " to top of tower " <<  B << endl;
 	  	HanoiTower(n-1,C,B,A);
  	}
}

运行时间正比于输出的信息行数目，而信息行数目等于碟子移动的次数，可得到碟子移动次数的递归式moves(n)
$$moves(n)=\{\begin{array}{l}0n=0\\ 2moves(n-1)+1n>0\end{array}$$

使用栈求解汉诺塔问题

假如要求显示出每次移动之后三座塔的布局（即塔上的碟子和它们从底到顶的次序），因此可以把每个塔表示成一个栈。

//全局变量，tower[1:3]表示三个塔
arrayStack<int> tower[4];

void moveAndShow(int,int,int,int);

void towerOfHanoi(int n)
{//函数moveAndShow的预处理程序
	for(int d = n;d > 0;d++)
		tower[1].push(d);
	
	//把n个碟子从塔1移到塔3，用塔2作为中转站
	moveAndShow(n,1,2,3);
}
void moveAndShow(int n,int x,int y,int z)
{
	if(n > 0)
	{
		moveAndShow(n-1,x,z,y);
		int d = tower[x].top();
		tower[x].pop();
		tower[y].push(d);
		showState();
		moveAndShow(n-1,z,y,x);
	}
}

列车车厢重排

一列货运列车有n节车厢，每节车厢要停靠在不同的车站。n个车站从1到n编号，货运列车车厢的编号要与他们停靠的编号相同。列车车厢重排在一个转轨站上进行，转轨站有一个入轨道，一个出轨道，和k个缓冲轨道。图示如下

其中H1,H2,H3均为栈。
对上图分析，首先3号车厢不能出轨，进入H1缓冲，之后6号6号不能出轨，但是也不能放在3之上，因为若放在3之上顺序错误，6放入H2，之后同理9放入H3,2号放入H1最合适，因为3号是比他大的最小的数字(3,6,9中)，依次放入，现在轨道排列如下

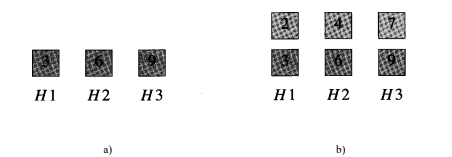
设计程序的思路，应该是，用一个数字记录应该出轨的车厢，然后让入轨道的车厢依次进入，如果他的编号等于应该出轨的编号，则出轨，出轨时应该继续判断是否现在的缓冲轨道中是否有能出轨的编号；否则进入缓冲轨道，当缓冲轨道无法进入时，失败。所有车厢输出成功，则成功。
代码实现如下

arrayStack<int> *track;   //缓冲轨道数组
int numberOfCars;
int numberOfTracks;
int smalllestCars;    //在缓冲轨道中编号最小的车厢
int itsTrack;     //停靠着最小编号车厢的缓冲轨道

bool railroad(int inputOrder[],int theNumberOfCars,int theNumberOfTracks)
{//从初始排序开始重排车厢
//如果重排成功，返回true，否则返回false

numberOfCars = theNumberOfCars;
numberOfTracks = theNumberOfTracks;

//创建用于缓冲轨道的栈
track = new arrayStack<int>[numberOfTracks + 1];

int nextCarToOutput = 1;
smallestCar = numberOfCars + 1;  //缓冲轨道中无车厢

//重排车厢
for(int i = 1;i <= numberOfCars; i++)
if(inputOrder[i] == nextCarToOutput)
{//将车厢inputOrder[i]直接移出到轨道
	cout << "Move car " << inputOrder[i]
		 << " from input track to output track" << endl;
	nextCarOutput++;

	//从缓冲轨道移到出轨道
	while(smallestCar == nextCarToOutput)
	{
		outputFromHoldingTrack();
		nextCarToOutput++;
	}
}
else
//将车厢inputOrder[i]移到一个缓冲轨道
	if(!putInHoldingTrack(inputOrder[i]))
		return false;
return true;
}

void outputFromHoldingTrack()
{//将编号最小的车厢从缓冲轨道移到出轨道
	//从栈itsTrack中删除编号最小的车厢
	track[itsTrack].pop();
	cout << "Move car "<<smallestCar <<" from holding "
		 <<"track " << itsTrack <<" to output track" << endl;
	
	//检查所有的栈顶，寻找编号最小的车厢和他所属的栈itsTrack
	smallestCar = numberOfCars + 2;
	for (int i = 1; i <= numberOfTracks; i++)
		if (!track[i].empty() && (track[i].top() < smallestCar))
		{
			smallestCar = track[i].top();
			itsTrack = i;
		}
}
bool putInHoldingTrack(int c)
{//将车厢c移到一个缓冲轨道。返回false，当且仅当没有可用的缓冲轨道

	//为车厢c寻找最合适的缓冲轨道
	//初始化
	int bestTrack = 0;  //目前最合适的缓冲轨道
	bestTop = numberOfCars + 1;  //取bestTrack中顶部的车厢
	
	//扫描缓冲轨道
	for(int i = 1;i <= numberOfTracks;i++)
		if(!track[i].empty())
		{//缓冲轨道i不为空
			int topCar = track[i].top();
			if (c < topCar && topCar < bestTop)
			{//缓冲轨道i的栈顶具有编号更小的车厢,比c大的最小的编号
				bestTop = topCar;
				bestTrack = i;
			}
		}
		else//缓冲轨道i为空
			//为甚在bestTrack == 0 时判断是因为避免多占空位的空间
			if(bestTrack == 0)bestTrack = i;
	
	if (bestTrack == 0)return false;  //没有可用的缓冲轨道
	
	//把车厢c移到轨道bestTrack
	track[bestTrack].push(c);
	cout << "Move car " << c << " from input track "
	     <<"to Holding track " << bestTrack <<< endl;
	
	//如果有需要更新smallestCar和itsTrack
	if(c < smallestCar)
	{
		smallestCar = c;
		itsTrack = bestTrack;
	}
}

开关盒布线

在开关盒布线问题中，给定一个矩形布线区域，其外围有若干管脚。两个管脚之间通过布设一条金属线路来连接。这条金属线路称为电线，它被限制在矩形区域内。两条电线交叉会发生电流短路。因此，电线不需交叉。每对要连接的管脚称为一个网组。例如一个有8个管脚和四个网组，四个网组分别是(1,4),(2,3),(5,6),(7,8)。因为这四个网组之间可以没有交叉，所以这个开关盒称为可布线开关盒。

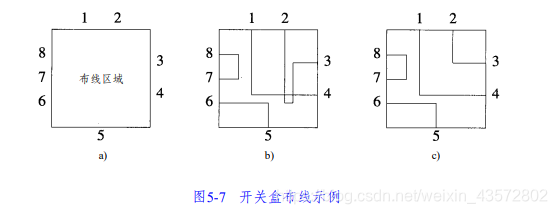
为了解决开关盒布线问题，我们注意到，当一个网组互连时，连线把布线区域分隔成两个分区，分区边界上的管脚属于哪一个分区与连线无关，而与互联网组的管脚有关，例如，当网组(1,4)互连时，就有两个分区。一个分区包含管脚2和3，另一个分区包含管脚5~8,。现在如果有一个网组，其两个管脚分别属于两个不同的分区，那么这个网组是不可布线的，进而整个开关盒布线实例也是不可布线的。如果没有出现这样的网组，那么就可根据连线不可跨区的原则，对每个分区是否可独立布线的问题作出判断，如果从一个分区中选择一个网组，这个网组把其所属分区分成两个子分区，而其余任一个网组的两个管脚都分属不同的子分区，那么就可以判断，这个分区是可布线的。
为了实现上述策略，可以按照顺时针或逆时针的方向沿着开关盒的外围进行遍历，可以从任意一个管脚开始。例如，如果按顺时针方向从针脚1开始遍历上图，那么将依次检查1,2,…,8。针脚1和4属于同一个网组，那么在针脚1至针脚4之间出现的所有针脚构成了第一个分区，而在针脚4至针脚1之间出现的所有针脚构成了第二个分区，把针脚1放入堆栈，然后继续处理，直至遇到针脚4。这个过程使我们仅在处理完一个分区之后才能进入下一个分区，下一个针脚是针脚2，它与针脚3同属一个网组，他们又把当前分区分成两个子分区。与前面的做法一样，把针脚2放入堆栈，然后继续处理直至遇到针脚3。由于针脚3和针脚2同属一个网组，而针脚2正处在栈顶，这表明已经处理完一个子分区，因此可将针脚2从栈顶删除。接下来遇到针脚4，由于与之互联的针脚1处在栈顶，因此当前的分区已经处理完毕，可以从栈顶删除针脚1.按照这种方法继续进行，直至检查完八个针脚，堆栈变空，所创建额分区都已处理完毕为止。
代码如下

bool checkBox(int net[],int n)
{//确定开关盒是否可布线
//数组net[0...n-1]管脚数组，用以形成网组
//n是管脚个数
	arrayStack<int> *s = new arrayStack<int>(n);

	//按顺时针扫描网组
	for(int i = 0;i < n;i++)
		//处理管脚i
		if(!s->empty())
			//检查栈的顶部管脚
			if(net[i] == net[s->top()])
				//管脚net[i]是可布线的，从栈中删除
				s->pop();
			else s->push(i);
		else s->push(i);

	//是否有剩余的不可布线的管脚
	if(s->empty())
	{//没有剩余的管脚
		cout << "Switch box is routable" << endl;
		return true;
	}
	cout << "Switch box is not routable" << endl;
	return false;
}

离线等价类问题

离线等价类问题输入是元素数目n，关系对数目r以及r个关系对。目标是把n个元素划分为等价类
求解分为两个阶段。在第一个阶段，我们输入数据，建立n个表以表示关系对。对每一个关系对，i放在list[j]，j放在list[i]。
假定n=9，r=11，且11个关系对是(1,5),(1,6),(3,7),(4,8),(5,2),(6,5),(4,9),(9,7),(7,8),(3,4),(6,2)。9个表是
list[1]=[5,6] list[2]=[5,6] list[3]=[7,4] list[4]=[8,9,3] list[5]=[1,2,6] list[6]=[1,2,5] list[7]=[3,9,8] list[8]=[4,7] list[9]=[4,7]
第二个阶段是寻找等价类。为寻找一个等价类，首先要找到该等价类中第一个没有输出的元素。这个元素作为该等价类的种子。该种子作为等价类的第一个成员输。从这个等价类开始，找出该等价类的所有其他成员。种子被加到一个表unprocessedList中。从表unprocessedList中删除一个元素i，然后处理表list[i]。list[i]中所有元素和种子同属一个类；将list[i]中还没有作为等价类成员的元素输出，然后加入unprocessedList中，这是一个过程：从表unprocessedList中删除一个元素i，然后把表list[i]中还没有输出的元素输出，并且加入unprocessedList中，这个过程持续到unprocessedList为空。这是我们就找到了一个等价类，然后继续寻找下一个等价类的种子。

int main()
{
	int n,
		r;
	
	cout << "Enter number of elements"<<endl;
	cin >> n;
	if(n < 2)
	{
		cout << "Too few elements" << endl;
		return 1;
	}
		
	cout << "Enter number of relations"<<endl;
	cin >> r;
	if(r < 1)
	{
		cout << "Too few relations"<<endl;
		return 1;
	}
	//建立空栈组成的数组，stack[0]不用
	arrayStack<int> * list = new arrayStack<int> [n+1];
	//输入r个关系，存储在表中
	int a,b;//(a,b)是一个关系
	for(int i = 1;i <= r;i++)
	{
		cout << "Enter next relation/pair" << endl;
		cin >> a >> b;
		list[a].push(b);
		list[b].push(a);
	}

	//初始化以输出等价类
	arrayStack<int> unprocessedList;
	bool* out = new bool[n+1];
	for(int i = 1;i <= n;i++)
		out[i] = false;
	//输出等价类
	for(int i = 1;i <= n;i++)
		if(!out[i])
		{//启动一个新类
			cout << "Next class is: " << i <<" ";
			out[i] = true;
			unprocessedList.push(i);
			//从unprocessedList中取类的剩余元素
			while(!unprocessedList.empty())
			{
				int j = unprocessedList.top();
				unprocessedList.pop();
				//表list[i]中的元素属于同一类
				while(!list[j].empty())
				{
					int q = list[j].top();
					list[j].pop();
					if(!out[q])//未输出
					{
						cout << q <<" ";
						out[q] = true;
						unprocessedList.push(q);
					}
				}
			}
			cout << endl;
		}
		cout << "End of list of equivalence classes"<<endl;		
}

迷宫老鼠

迷宫是一个矩形区域，有一个入口和一个出口，迷宫内部包含不可翻越的墙壁或障碍物。这些障碍物沿着行和列放置，与迷宫的边界平行。迷宫的入口在左上角，出口在右下角

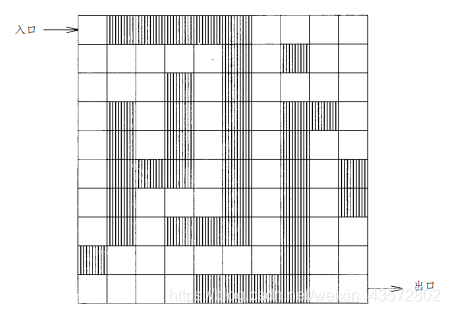
假定用n×m的矩阵来描述迷宫，矩阵的位置(1,1)表示入口，(n,m)表示出口，n和m分别代表迷宫的行数和列数。有障碍为1，无障碍为0，迷宫老鼠问题是要寻找一条从入口到出口的路径，路径
是一个由位置组成的序列，每一个位置都没有障碍，而且除入口外，路径上的每个位置都是前一个位置在东、西、南、北方向上相邻的一个位置。

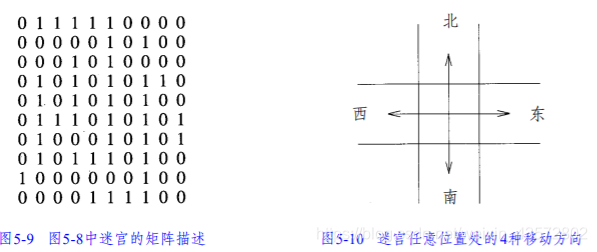
首先把位置 ( 1 , 1 )放入堆栈，并从它开始进行搜索。由于位置( 1 , 1 )只有一个空闲的邻居( 2 , 1 )，所以接下来将移动到位置( 2 , 1 )，并在位置( 1 , 1 )上放置障碍物，以阻止稍后的搜索再次经过这个位置。从位置 ( 2 , 1 )可以移动到( 3 , 1 )或( 2 , 2 )。假定移动到位置( 3 , 1 )。在移动之前，先在位置( 2 , 1 )上放置障碍物并将其放入堆栈。从位置 ( 3 , 1 )可以移动到( 4 , 1 )或( 3 , 2 )。假定移动到位置( 4 , 1 )，则在位置( 3 , 1 )上放置障碍物并将其放入堆栈。从位置 ( 4 , 1 )开始可以依次移动到(5,1) 、(6,1) 、( 7 , 1 )和( 8 , 1 )。到了位置( 8 , 1 )以后将无路可走。此时堆栈中包含的路径从( 1 , 1 )至( 8 , 1 )。为了探索其他的路径，从堆栈中删除位置 ( 8 , 1 )，然后回退至位置( 7 , 1 )，由于位置( 7 , 1 )也没有新的、空闲的相邻位置，因此从堆栈中删除位置 ( 7 , 1 )并回退至位置( 6 , 1 )。按照这种方式，一直要回退到位置 ( 3 , 1 )，然后才可以继续移动（即移动到位置（ 3 , 2））。注意在堆栈中始终包含从入口到当前位置的路径。如果最终到达了出口，那么堆栈中的路径就是所需要的路径。
为了避免在处理内部位置和边界位置时存在差别，可以在迷宫的周围增加一圈障碍物。

求为代价的。
可以用行号和列号来指定每个迷宫位置，行号和列号被分别称之为迷宫位置的行坐标和列坐标。可以定义一个相应的类 Position来表示迷宫位置，它有两个私有成员row和col。

bool FindPath()
{//从位置(1,1)到出口(m,m)路径增加一圈障碍物；
//对跟踪当前位置的变量进行初始化
	Position here;
	here.row = 1;
	here.col = 1;

	maze[1][1] = 1;//阻止返回入口
	//寻找通往出口的路径
	while(不是出口)do{
		选择一个相邻位置;
		if(存在这样一个相邻位置){
			把当前位置here放入堆栈
			//移动到相邻位置，并在该位置放上障碍物
			here = neighbor;
			maze[here.row][here.col]=1;}
			else{
			//不能继续移动，需回溯
			if(堆栈path为空)return false;
			回溯到path栈顶中的位置here;
			}
			return true;
		}
	}	
}

对于位置here，下一步将移动到它的哪一个相邻位置。如果难找固定的方案选择可行的位置，将可以使问题得到简化。例如，可以首先尝试向右移动，然后是向下，向左，最后是向上。

bool FindPath()
{// 寻找从位置(1,1)到出口(m,m)的路径
 //如果成功则返回true，否则返回false
 //如果内存不足，引发异常NoMem
 	path = new Stack<Position>(m * m - 1);
 	//对偏移量进行初始化
 	Position offset[4];
 	offset[0].row = 0;offset[0].col = 1;//右
 	offset[1].row = 1;offset[1].col = 0;//下
 	offset[2].row = 0;offset[2].col = -1;//左
 	offset[3].row = -1;offset[3].col = 0;//上
 	//在迷宫周围增加一圈障碍物
 	for(int i = 0;i <= m + 1;i++){
 		maze[0][i] = maze[m+1][i] = 1;//底和顶
 		maze[i][0] = maze[i][m+1] = 1;//左和中
 	}
 	Position here;
 	here.row = 1;
 	here.col = 1;
 	maze[i][i] = 1;//阻止返回出口
 	int option = 0;
 	int LastOption = 3;
 	//寻找一条路径
 	while(here.row != m || here.col != m){//不是出口
 		//寻找并移动到一个相邻位置
 		int r,c;
 		while(option <= LastOption){
 			r = here.row + offset[option].row;
 			c = here.col + offset[option].col;
 			if(maze[r][c] == 0) break;
 			option++;
 		}
 		//找到一个相邻位置了吗?
 		if(option <= LastOption){//移动到maze[r][c]
 			path->push(here);
 			here.row = r;here.col = c;
 			//设置障碍物以组织再次访问
 			maze[r][c] = 1;
 			option = 0;
 		}
 		else{//没有可用的相邻位置，回溯
 			if(path->isEmpty())return false;
 			Position next = path->top();
 			path->pop();
 			if(next.row = here.row)
 			//从next走到的here
 			//这个从栈顶中的位置的选择和自己设计的行走方案有关
 			//走的位置是上一次到这个位置，下一个方向的位置
 				option = 2 + next.col - here.col;
 			else option = 3 + next.row - here.row;
 			here = next;
 		}
 	}
 	return true;//到达迷宫出口
}

FindPath首先创建一个足够大的堆栈* path，然后对偏移量数组进行初始化，并在迷宫周围增加一圈障碍物。在while循环中，从当前位置here出发，按下列次序来选择下一个移动位置：向右、向下、向左和向上。如果能够移动到下一个位置，则将当前位置放入堆栈 path，并移动到下一个位置。如果找不到下一个可以移动的位置，则退回到前一个位置。如果无法回退一个位置（即堆栈为空），则表明不存在通往出口的路径。当回退至堆栈的顶部位置 (next)时，可以重新选择另一个可能的相邻位置，这可以利用 next和here来推算。注意here是next的一个邻居。对下一个移动位置的选择可用以下代码来实现：

	Position next = path->top();
 	path->pop();
 	if(next.row = here.row)//这个从栈顶中的位置的选择和自己设计的行走方案有关
 	//走的位置是上一次到这个位置，下一个方向的位置。设计的顺序为右下左上
 		option = 2 + next.col - here.col;//行相同，next.col - here.col=1说明现在是向左option=2，下一个为向上option=3，
 	else option = 3 + next.row - here.row;
 	here = next;