核磁共振成像基本原理——杨正汉（1）

1. MRI仪硬件基本知识

1.1 主磁体

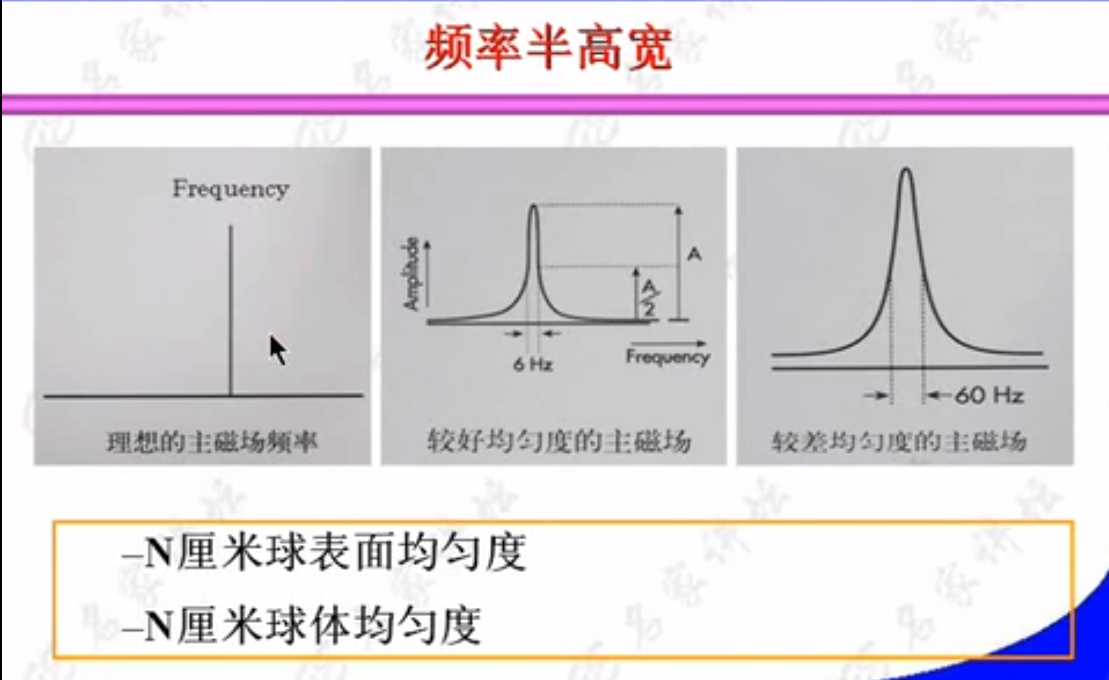
2. 梯度系统

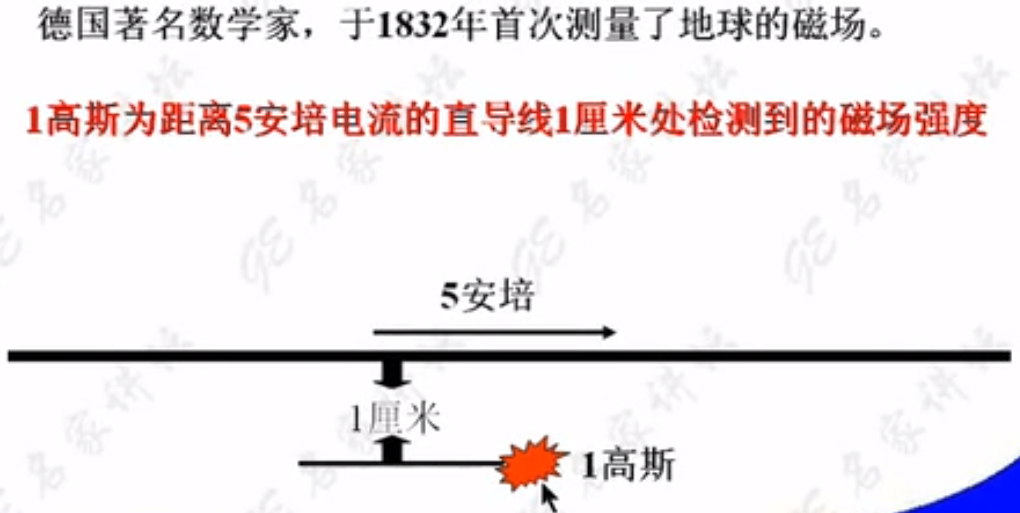
在头部电流线圈产生的磁场与主磁场一致，故加强了磁场强度，在脚步电流线圈产生的磁场方向与主磁场相反，故减少了磁场强度。

1.3 射频系统

1.4 计算机系统及谱仪

2. MRI成像的物理学原理

2.1 人体MR成像的物质基础

2.2 在磁场中的宏观磁化矢量

MRI不能检测微观的磁化矢量，怎么检测宏观的磁化矢量呢？把人体放进大磁场即可。
杂乱无章的小磁场就会受大磁场影响，变得很有序。有两种状态：一个是与大磁场方向（H原子能级太小，产生的磁场太小了，反抗不了）一致，一个是与大磁场方向（H原子原子能级大，产生的磁场太大了，可以反抗）相反。因为人体内能量低的H原子占多数，总体抵消后产生的磁化矢量为纵向磁化矢量。

答案是否定的

氢质子在旋转的时候，横向磁化矢量被抵消了，如下图。


结论

2.3 MRI可以探测出什么磁化矢量呢？

因为纵向磁化矢量相对于主磁场还是太小了。

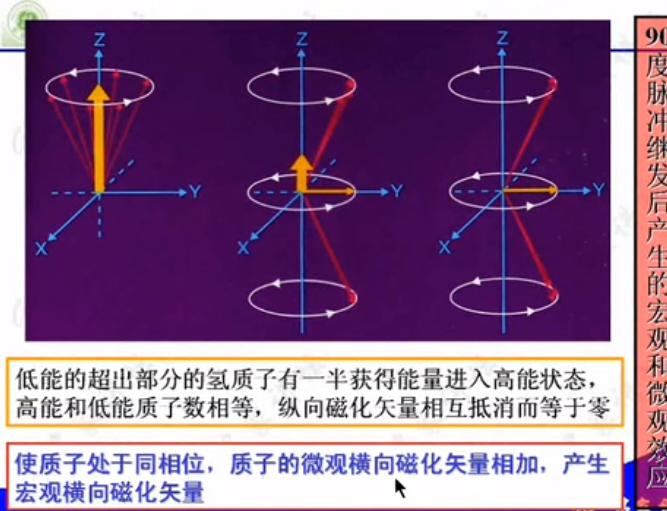
2.4 射频线圈关闭后采集信号

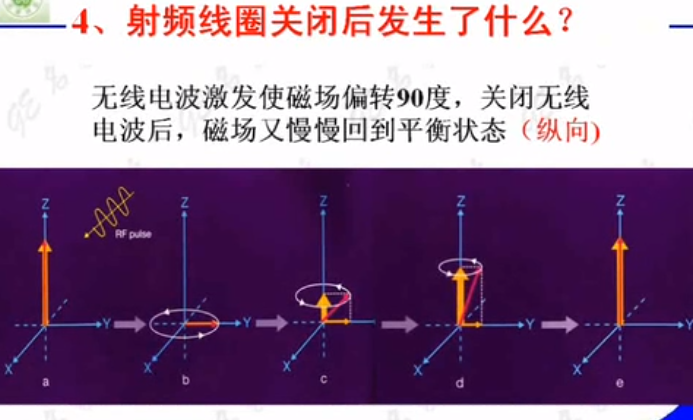
失相位是指：氢质子的位置不再统一了，而是随机地分在每个位置，横向磁化矢量就逐渐消失。

2.5 磁共振加权成像

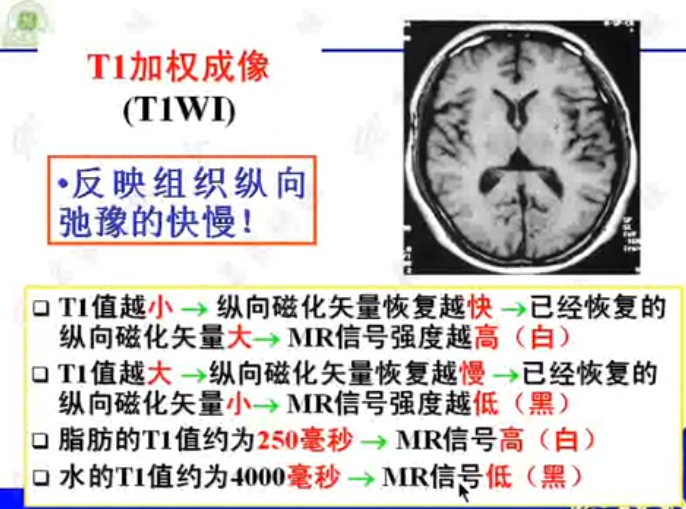
T1加权成像是以纵向磁化矢量为准，那怎么探测呢？
利用脉冲信号，将T1得到的纵向磁化矢量转为横向磁化矢量后，立马采集即可。

3. MRI空间定位

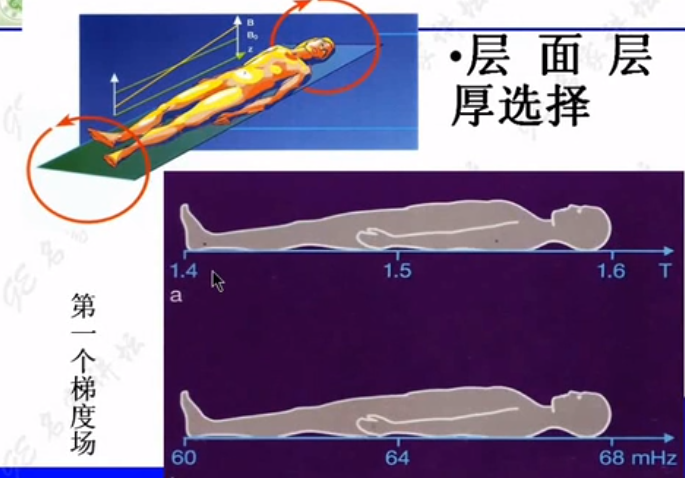
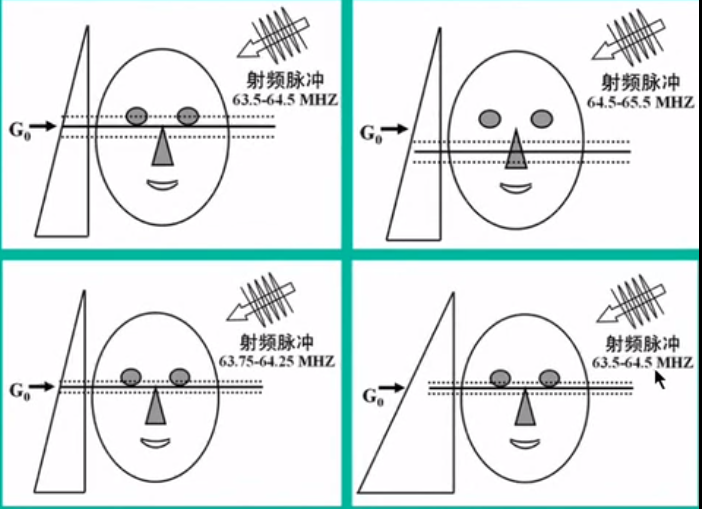
MR线圈是探测每一层的信息，那怎么对应像素呢？

假设一层图像为3X3,就9个像位点，添加梯度场后，即右高左低的梯度场，每个像素的进度频率变化了。

我们只考虑3个像素，添加一个前高后低的梯度场，他们的进度频率不同，进度快的相位跑到前面去，进度慢的在后面；
这时候，然后关掉相位梯度场，等他们的进度频率一致时，但是相位被保留了下来。

第一个相位梯度场可以采集第一个和第二个（相反）；第二个梯度场可以采集第一个和第三个信号，。。。

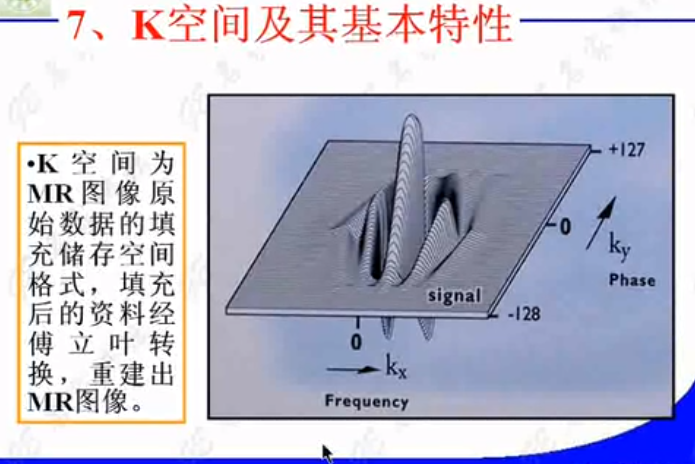
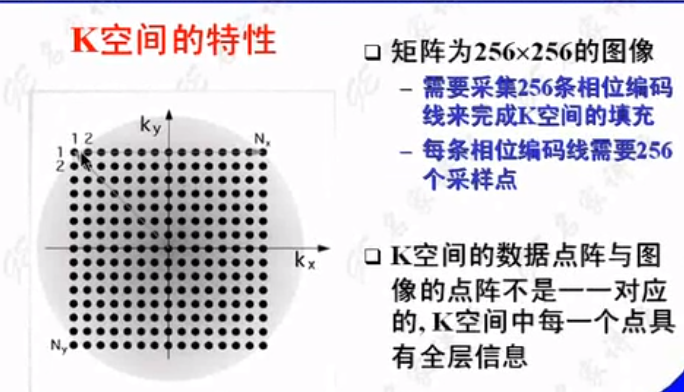
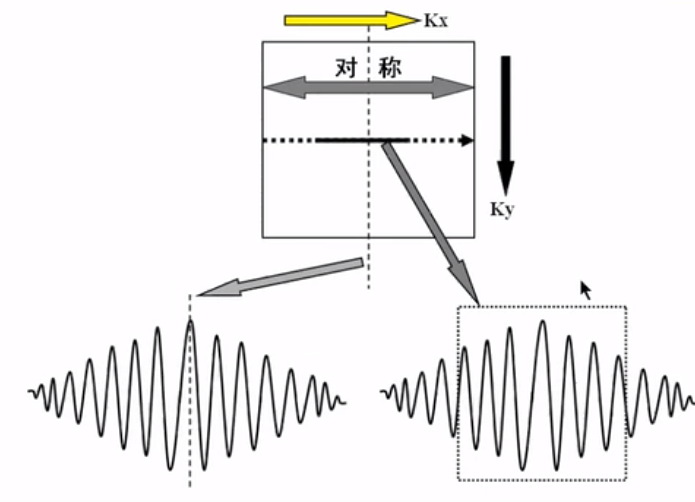
从K空间角度总结MRI成像的过程：